概述

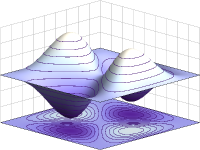
在无限深方形阱里，两个全同费米子的反对称性波函数绘图。

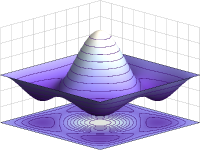
在无限深方形阱里，两个全同玻色子的对称波函数绘图。

假若两个可以被区分的粒子分别位于 r a {\displaystyle \mathbf {r} _{a}} 、 r b {\displaystyle \mathbf {r} _{b}} ，分别处于量子态 ψ ψ --> 1 {\displaystyle \psi _{1}} 、 ψ ψ --> 2 {\displaystyle \psi _{2}} ，则描述这两个粒子的总波函数为 ψ ψ --> 1 ( r a ) {\displaystyle \psi _{1}(\mathbf {r} _{a})} 、 ψ ψ --> 2 ( r b ) {\displaystyle \psi _{2}(\mathbf {r} _{b})} 的简单乘积：

其中， ψ ψ --> ( r a , r b ) {\displaystyle \psi (\mathbf {r} _{a},\mathbf {r} _{b})} 为总波函数，注意到第一个参数是第一个粒子的位置，第二个参数是第二个粒子的位置。

假若将这两个粒子的位置彼此相互对调，则描述这两个粒子的总波函数变为

现在，假设这两个粒子是全同粒子，不可以区分到底哪个粒子是第一个粒子，哪个粒子是第二个粒子；更详细地说，做任何实验都无法分辨出哪个粒子是哪个粒子。对于粒子位置交换，这两个粒子的概率密度应该具有不变性：

但是上述两种总波函数的形式都不具有这种不变性，只有以下两种总波函数的形式可以满足不变性。一种是对称性总波函数：

另一种是反对称性总波函数：

从反对称性总波函数的形式可以推论，假设描述两个全同粒子的总波函数对于粒子交换具有反对称性，并且它们在同时刻处于同样量子态：

则它们的概率密度恒等于零，找到它们处于同样量子态的概率为零，因为总波函数等于零：

费米子的自旋为半整数；描述两个全同费米子的总波函数对于粒子交换具有反对称性。因此，两个费米子在同一个量子系统中永远无法占据同一量子态，这称为泡利不相容原理。并没有涉及到任何位势，并没有任何作用力施加于它们本体，这纯粹是从无法区分全同粒子而产生的一种量子性质，在经典物理学里，找不到类似性质。

费米子包括像夸克、电子、中微子等等基本粒子，另外，由三个夸克结合形成的亚原子粒子，像质子、中子等等，也都是费米子。它们必须用费米–狄拉克统计来描述它的统计行为。

原子是一种复合粒子，原子到底是费米子还是玻色子，必需依总自旋而定。例如，氦-3的总自旋为1/2，它含有两个自旋相反的质子、一个任意自旋的中子、两个自旋相反的电子，所以它是费米子；而氦-4的总自旋为0，它含有两个自旋相反的质子、两个自旋相反的中子、两个自旋相反的电子，所以它是玻色子。

氦-2拥有两个束缚电子，描述这两个电子的基态需要用到四个量子数（ n , ℓ ℓ --> , m ℓ ℓ --> , m s {\displaystyle n,\ell ,m_{\ell },m_{s}} ），其数值分别为（1,0,0,-1/2）和（1,0,0,+1/2），唯一不同之处为自旋磁量子数 m s {\displaystyle m_{s}} ：-1/2和+1/2，分别代表电子在原子轨道中的自旋为上旋和下旋，即每一原子轨道最多只能容纳自旋相反的两个电子。泡利不相容原理主导原子的电子排布问题，从而直接影响到日常物质的各种性质，从大尺度稳定性至原子的化学行为。

玻色子的自旋为整数，总波函数对于粒子交换具有对称性，不遵守泡利不相容原理。玻色子可以共处于相同的量子态。玻色子包括光子、胶子、促成物质超导性质的库柏对、W及Z玻色子等等。玻色子必须用玻色-爱因斯坦统计来描述它的统计行为。

历史

早期雏论

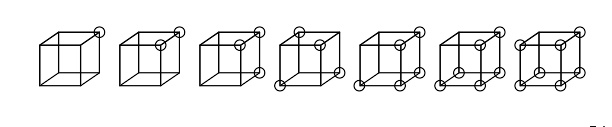
路易斯提出的立方体原子模型。

20世纪早期，学者们渐渐发现，假若原子或分子的束缚电子数量是偶数，而不是奇数，则这原子或分子会更具化学稳定性（chemical stability）。1914年，约翰内斯·里德伯建议，主量子数为 n {\displaystyle n} 的电子层最多只能容纳 2 n 2 {\displaystyle 2n^{2}} 个电子，但是他并不清楚为什么在这表达式里会出现因数 2 {\displaystyle 2} 。

1916年，吉尔伯特·路易斯在论文《原子与分子》（The atom and the Molecule）里提出“立方原子模型”的假说，他表示，原子倾向于在每个电子层里维持偶数量的电子，更特别倾向于维持8个电子对称性地排列于立方体的8个顶点。至于电子怎样才能固定不动地停留在顶点，他认为，作用于几个非常邻近的粒子之间的电场力，不遵守简单的长距离平方反比定律。他并没有试图预测这模型会造成什么样的光谱线。任何模型的预测都必须符合实验结果，否则无法得到学术界的肯定。

化学家欧文·朗缪尔于1919年提议，每个电子层，按照半径尺寸，从小到大，比例为 1 : 2 : 3 : 4 … … --> {\displaystyle 1:2:3:4\dots } ；因此，按照面积大小，比例为 1 2 : 2 2 : 3 2 : 4 2 … … --> {\displaystyle 1^{2}:2^{2}:3^{2}:4^{2}\dots } ；每个电子层又切分为同样大小的小室，第n个电子层切分为 2 n 2 {\displaystyle 2n^{2}} 个同样大小的“小室”，每个小室都固定于原子的某个区域，除了最内部电子层的小室只能容纳1个电子以外，其它每个小室都可容纳2个电子。比较内部的电子层必须先填满，才可开始填入比较外部的电子层。朗缪尔并没有对于为什么每个小室只能容纳最多2个电子的论述给出说明，虽然他怀疑在这里面隐藏了一种双重对称。

1913年，尼尔斯·玻尔提出关于氢原子结构的波尔模型，成功解释氢原子线谱，他又试图将这理论应用于其它种原子与分子，但获得很有限的结果。经过漫长九年的研究，1922年，玻尔才又完成关于周期表内各个元素怎样排列的论述，并且建立了递建原理，这原理给出在各个原子里电子的排布方法──每个新电子会占据最低能量空位。但是，波尔并没有解释为什么每个电子层只能容纳有限并且呈规律性数量的电子，根据最小能量原理（principle of minimum energy），所有系统都趋向于最低能量态，因此所有束缚于原子的电子应该都被同样排列在最低能量的电子层。

反常塞曼效应的困惑

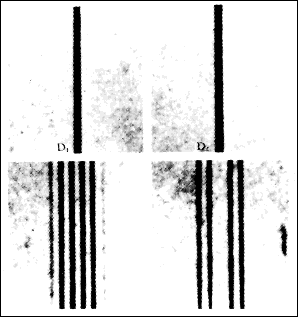
钠D线是因自旋-轨道作用而产生的双重线，分别是 P 1/2 态跃迁至 S 1/2 态、 P 3/2 态跃迁至 S 1/2 态，这两种跃迁方式所产生的谱线。施加弱外磁场而产生的反常塞曼效应会使这双重线出现更多分裂。

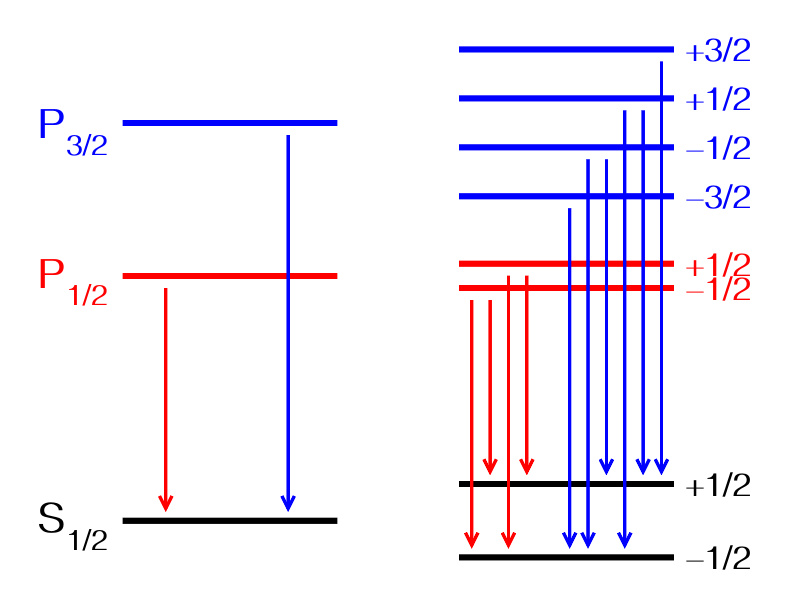
由于弱外磁场作用， S 1/2 态会分裂成两个亚态， P 1/2 态也会分裂成两个亚态，但由于两个态的朗德g因子不同，因此从 P 1/2 会形成4条不同谱线； P 3/2 态会分裂成四个亚态，但是从 P 3/2 的+3/2态不能跃迁至 S 1/2 的-1/2态，从 P 3/2 的-3/2态不能跃迁至 S 1/2 的+1/2态，因此从 P 3/2 总共会形成6条不同谱线。

泡利于1918年进入慕尼黑大学就读，阿诺·索末菲是他的博士论文指导教授，他们经常探讨关于原子结构方面的问题，特别是先前里德伯发现的整数数列 2 , 8 , 18 , 32 … … --> {\displaystyle 2,8,18,32\dots } ，每个整数是对应的电子层最多能够容纳的电子数量，这数列貌似具有特别意义。1921年，泡利获得博士学位，在他的博士论文里，他应用玻尔-索末非模型来研讨氢分子离子H 2 问题，因此他熟知旧量子论的种种局限。毕业后，泡利应聘在哥廷根大马克斯·玻恩·玻恩的得意助手。后来，玻尔邀请泡利到哥本哈根大学的玻尔研究所工作，专注于研究原子谱光谱学的反常塞曼效应。 在这段时期，他时常怏怏不乐，并且漫无目标地徘徊在哥本哈根市区内的大街小巷，因为反常塞曼效应给予他很大的困扰，他无法解释为什么会发生反常塞曼效应，这主要是因为经典模型与旧量子论埃尔温·薛定谔薛定谔的波动维尔纳·海森堡海森堡的矩阵力学还要等几年才会出现。泡利只能够分析出当外磁场变得非常强劲时的案帕邢即帕邢-巴克效应（Paschen-Backer effect），由于强外磁场能够破坏自旋角动量与轨道角动量之间的耦合，因此问题变得较为简单。这研究对于日后发现泡利原理具有关键性作用。

隔年，泡利任职为汉堡大学物理讲师，他开始研究电子层的填满机制，他认为这问题与多重线结构有关。按照那时由玻尔带头的主流观点，因为原子核具有有限角动量，才会出现双重线结构。泡利对此很不赞同，1924年，他发表论文指出，因为电子拥有一种量子特性，碱金属才会出现双重线结构（如右图所示，在无外磁场作用下得到的钠D线是典型的双重线结构），这是一种无法用经典力学理论描述的“双值性”。为此，他提议设置另一个量子数，这量子数的数值只可能是两个数值中的一个。

发现泡利不相容原理

从光谱线分裂的数据，爱德蒙·斯通纳（Edmund Stoner）最先给出各个原子的正确电子排布。他在1924年发表论文提议，将电子层分成几个电子亚层，按照角量子数 ℓ ℓ --> {\displaystyle \ell } ，每个电子亚层最多可容纳 2 ( 2 ℓ ℓ --> + 1 ) {\displaystyle 2(2\ell +1)} 个电子。斯通纳指出，在碱金属磁场的碱金属原子里，角量子数为 ℓ ℓ --> {\displaystyle \ell } 的价电子的能级会分裂成 2 ( 2 ℓ ℓ --> + 1 ) {\displaystyle 2(2\ell +1)} 个能级。 从这篇论文，泡利找到解释电子排列的重要线索，泡利敏锐地查觉到，每个填满的电子亚层都拥有 2 ( 2 ℓ ℓ --> + 1 ) {\displaystyle 2(2\ell +1)} 个电子，因为每一个电子都只能占据一个独特的量子态 ( n , ℓ ℓ --> , j , m j ) {\displaystyle (n,\ell ,j,m_{j})} ；其中， j {\displaystyle j} 是电子的总角量子数， m j {\displaystyle m_{j}} 是总磁量子数。给定角量子数 ℓ ℓ --> {\displaystyle \ell } ，则总角量子数 j {\displaystyle j} 的数值可以为 ℓ ℓ --> ± ± --> 1 / 2 {\displaystyle \ell \pm 1/2} 。对于每个总角量子数 j {\displaystyle j} ，总磁量子数 m j {\displaystyle m_{j}} 可以为 2 j + 1 {\displaystyle 2j+1} 种数值，从 j {\displaystyle j} ， j − − --> 1 {\displaystyle j-1} ， j − − --> 2 {\displaystyle j-2} ﹒﹒﹒到 − − --> j {\displaystyle -j} 。总合起来，每个电子亚层可以拥有 2 ( 2 ℓ ℓ --> + 1 ) {\displaystyle 2(2\ell +1)} 个电子。1925年，泡利发表论文正式提出泡利原理，以禁令的形式表示如下：

之后不久，撒姆尔·高斯密特（Samuel Goudsmit）与乔治·乌伦贝克表示，电子具有自旋，而这自旋与泡利所提到的第四个量子数的双值性密切相关。他们假设电子的自旋为 1 / 2 {\displaystyle 1/2} ，在磁场作用下，沿着磁场方向可以是上旋 + 1 / 2 {\displaystyle +1/2} 或下旋 − − --> 1 / 2 {\displaystyle -1/2} ，总角量子数 j {\displaystyle j} 是角量子数 ℓ ℓ --> {\displaystyle \ell } 与自旋量子数 s {\displaystyle s} 的代数和或代数差。应用这些概念，可以很容易说明反常塞曼效应。起初，泡利对于这点子持保留态度。后来，卢埃林·汤玛斯（Llewellyn Thomas）应用狭义相对论正确地计算出双重线结构。自旋模型因此得到肯定。

在泡利原理被发表的那年，海森堡创建了矩阵力学。隔年，薛定谔发展出波动力学。这两个创举标志了现代量子力学的诞生。后来，海森堡与狄拉克分别提出了全同粒子的概念。在经典力学里，可以单独地跟踪与辨认每一个粒子；在量子力学里，由于不确定性原理，无法准确的跟踪任何粒子，又由于在每一种粒子里，所有粒子都完全相同，无法辨认出哪个粒子是哪个粒子。因此，全同粒子的概念是精典力学与量子力学的一个重要分水岭。恩里科·费米与保罗·狄拉克分别独立地推导出遵守泡利不相容原理的多个全同粒子（费米子）的统计行为，称为费米-狄拉克统计。萨特延德拉·玻色与阿尔伯特·爱因斯坦先前合作给出的玻色-爱因斯坦统计则描述不遵守泡利不相容原理的多个全同粒子（玻色子）的统计行为。海森堡与狄拉克分别应用波动力学于多个粒子系统，泡利不相容原理的机制可以用波函数对于全同粒子交换的对称性与反对称性来说明。由于泡利不相容原理能够适用于所有费米子，狄拉克对于这个延伸给出命名“不相容原理”，指的是在量子系统里，多个全同费米子不能处于同样量子态。海森堡应用泡利不相容原理来说明金属的铁磁性与其他性质。

发现自旋统计定理

泡利的1925年论文并没有说明为什么自旋为半整数的费米子遵守泡利不相容原理，而自旋为整数的玻色子不遵守泡利不相容原理？1940年，泡利提出自旋统计定理尝试解释这问题， 这定理用相对论性量子力学展示出，由自旋为半整数的全同粒子所组成的量子系统，其波函数对于粒子交换具有反对称性，由自旋为整数的全同粒子所组成的量子系统，其波函数对于粒子交换具有对称性，泡利不相容原理是这量子行为的自然后果。

但是，实际而言，这定理只展示出了自旋与统计行为之间的关系符合相对论性量子力学，与所有已知物理理论没有任何矛盾。泡利于1947年承认，他无法对于泡利不相容原理给出一个逻辑解释，也无法从更基础理论推导出这原理，尽管他原本期望新创建的量子力学能够严格地推演出泡利不相容原理。 理查·费曼在著名的费曼物理学讲义里清楚表明，

想要找到这基本原因的物理学者至今仍旧无法得到满意答案！这基本原因很可能会是非常错综复杂，完全不像泡利不相容原理本身那样的简单与精致。

应用于广泛学术领域

保罗·埃伦费斯特于1931年指出，由于泡利不相容原理，在原子内部的束缚电子不会全部掉入最低能量的轨道，它们必须按照顺序占满能量越来越高的轨道。因此，原子会拥有一定的体积，物质也会那么大块。 1967年，弗里曼·戴森与安德鲁·雷纳德（Andrew Lenard）给出严格证明，他们计算吸引力（电子与核子）与排斥力（电子与电子、核子与核子）之间的平衡，推导出重要结果：假若泡利不相容原理不成立，则普通物质会坍缩，占有非常微小体积。

1964年，夸克的存在被提出之后不久，奥斯卡·格林柏格（Oscar Greenberg）引入了色荷的概念，试图解释三个夸克如何能够共同组成重子，处于在其它方面完全相同的状态但却仍满足泡利不相容原理。这概念后来证实有用并且成为夸克模型（quark model）的一部分。1970年代，量子色动力学开始发展，并构成粒子物理学中标准模型的重要成分。

重要应用

泡利不相容原理可用来解释很多种不同的物理现象与化学现象，这包括原子的性质，大块物质的稳定性与性质、中子星或白矮星的稳定性、固态能带理论里的费米能级等等。

原子的电子层结构与物理、化学性质

泡利不相容原理的重要后果是原子里错综复杂的电子层结构，以及原子与原子之间共用价电子的方式，这后果解释了各种不同的化学元素与它们的化学组合。电中性的原子含有数量相等的电子与质子。电子是费米子，遵守泡利不相容原理，每一个原子轨道最多只能载有2个电子。当正好有两个电子处于同一个原子轨道时，这对电子的自旋必定彼此方向相反。

举例而言，中性氦原子有两个束缚电子，这两个电子都能够占据最低能量原子轨道（），但彼此之间自旋的方向相反，一个是上旋，另一个是下旋。由于自旋是电子量子态的一部分，这两个电子处于不同的量子态，不会违反泡利不相容原理。中性锂原子有三个束缚电子，第三个电子不能占据原子轨道，因为原子轨道已被填满，只能改而占据第二低能量原子轨道（2s）。类似地，越后面元素的束缚电子必须占据越高能量的原子轨道。每一个元素的化学性质与最外层的电子层所拥有电子的数量有关。不同的元素，假若最外层的电子层所拥有电子的数量相同，则所表现出的性质类似，周期表就是依赖这机制来排列元素。

倚赖泡利不相容原理与递建原理，就可以解释周期表内大多数元素的物理与化学性质，但是，遇到关于比较某些原子轨道的能量高低问题，需要使用到洪德规则。较重元素可能会出现不遵守洪德规则的例外。

物质稳定性

类氢原子系统的稳定性并不倚赖泡利不相容原理，而是倚赖描述原子的量子理论。应用经典电动力学来分析类氢原子稳定性问题，由于库仑力作用，束缚电子会被原子核吸引，呈螺线运动掉入原子核，同时发射出无穷大能量的辐射，因此可以推论，原子不具有稳定性。但是，在大自然里这假想现象实际并不会发生。那么，为什么氢原子的束缚电子不会掉入原子核？从薛定谔方程，可以计算出氢原子系统的基态能量大于某有限值，因此不可能发射出无穷大能量的辐射，自然也不会掉入原子核。另外，也可以应用海森堡不确定性原理 Δ Δ --> x Δ Δ --> p ≥ ≥ --> ℏ ℏ --> / 2 {\displaystyle \Delta x\Delta p\geq \hbar /2} 来启发性地说明这问题，电子越接近原子核，电子动能越大。但是海森堡不确定性原理不能严格给出数学证明，必需使用类似的索博列夫不等式。 详尽细节，请参阅条目氢原子稳定性。

泡利不相容原理使得含有多个电子与核子的大型系统占有大体积的空间，并且具有稳定性。对于这论题，埃伦费斯特曾经提出疑问，为什么物质会这么大块，尽管它的分子与原子被包装地那么紧密？追根究柢，为什么原子的尺寸会这么庞大？举例而言，铅原子拥有82个质子与82个电子，铅原子核的吸引力应该很强，是氢原子核的82倍，但是只有少数电子的轨道离原子核很近，按照经典理论，在电子与电子之间的排斥力超过原子核的吸引力以前，应该可以有更多电子集中在原子核附近的轨道。但是，为什么铅原子不会这样坍缩变小？埃伦费斯特猜想，这是因为泡利不相容原理所产生的效应；由于泡利不相容原理，原子的尺寸才会这么庞大，物质才会这么大块。后来，戴森发表论文表明，假若没有泡利不相容原理，不只单独原子会坍缩变小，物质也会同样的坍缩变小；任意两个大块物体混合在一起，就会释出像原子弹爆炸一般的能量！

假设一个原子拥有N>2个电子，由于电子是费米子，这N个电子不能占有同样量子态，因此不会都塌陷至最低能量的量子态，电子排布不会是() ；假若泡利不相容原理不成立，则所有电子都会塌陷至轨道，原子的尺寸会变得很小；除了与原子核的电荷平方成电离能电离能以外，元素与元素之间不会有什么显著差别；元素越重，化学反应越需要更多的能量；元素的性质不会出现周期性；化学与生物学都成为空论，更不会有任何地球生命！

冷恒星稳定性

在天文学里，白矮星与中子星的存在演示出泡利不相容原理的惊奇效应。在这两种冷恒星天文物体里，原子结构被特强劲的引力破坏，但仍旧能够依靠简并压维持平衡。这种奇特形式的物质称为简并物质。恒星通常倚靠内部的核聚变来与质量产生的巨大引力维持平衡。白矮星不会进行核聚变，因此必须依靠电子简并压来与引力相对抗。在中子星里，由于受到更强劲的引力，电子与质子融合在一起，形成中子。虽然作用距离较短，中子能够产生更强劲的简并压，因此促使中子星达到稳定状况，不再进一步坍缩，尽管如此，中子星的尺寸比白矮星小，密度比白矮星高。中子星是已知最刚硬的物体，其杨氏模量（更精确地，体积模量）比钻石还刚硬20个数量级。但是，甚至这么刚硬的物体仍旧可以被大质量恒星的引力场或超新星所瓦解，导致黑洞的形成。

凝聚态性质

经典自由电子理论描述一群价电子在固态金属的晶体结构里的物理行为。按照这理论，原本束缚于金属原子的价电子自由地移动于固定不动的离子，成为自由电子，假定它们是遵守麦克斯韦-玻尔兹曼分布的自由电子气体，则可用气体运动论来研究相关问题。经典自由电子理论可以用来论述维德曼–夫兰兹定理，即金属的热导率与电导率之间的比例与温度有关，也可以推导出欧姆定律的形式；但是，它给出的电导率与温度之间的关系不符合实验结果，它预测比热与温度无关，而实验证实在低温状况比热与温度成正比。由于经典理论使用的是麦克斯韦-玻尔兹曼分布，所以会推导出这些错误结果。

量子自由电子理论引入量子力学概念来对经典理论加以改善。在金属内部的价电子被模拟为被包围在一个三维盒子内部的粒子，虽然能够自由移动于盒子内部，它永远不能逃离到盒子外部。由于电子是费米子，遵守泡利不相容原理，每个电子只能占有一个独特的量子态，在这里称为“轨道”，则电子的量子行为必需用费米–狄拉克统计来描述。通过解析盒中粒子问题的薛定谔方程，应用泡利不相容原理，可以获得基态系统的电子数量与费米能之间的关系，每一个能量不高于费米能的轨道都被电子填满，每一个能量高于费米能的轨道都是空的。这个温度为绝对零度的系统，假设经过加热使得温度增加，则不是所有电子都能够获得能量，而是只有能量在费米能级附近的电子能够获得能量， 这可以从在不同温度的费米-狄拉克分布图观察得知，这一小部分能够获得能量的电子的数量与温度成正比，所以在低温状况比热与温度成正比，这机制也可说明金属的比热所展现出的相当微小的数值。 一般而言，量子自由电子理论对于比热、热导率、电导率、磁化率等等现象都给出了大量论述，但是，它仍旧无法对于某些重要问题给出满意说明，例如，对于金属、半金属、半导体、绝缘体等等物质的辨别，对于霍尔系数的正数值。若要合理解释这些问题，还需要更先进、更精致的理论。

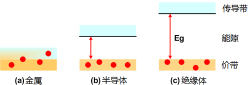
金属的价带与传导带之间没有距离，因此电子（红色实心圆圈）可以自由移动。绝缘体的带隙宽度最大，电子难以从价带跃迁至传导带。半导体的带隙宽度在两者之间，电子较容易跃迁至传导带。

量子自由电子理论忽略了离子的存在，但是离子对于整个系统的实际影响很大。根据能带理论，固定于晶格位置的离子会产生周期性位势，因此标志性地形成能带区域与带隙区域，电子的能量允许在能带区域内，禁止在带隙区域内。按照泡利不相容原理，每个电子只能占有一个轨道，能量较低的轨道先被占据，能量较高的轨道才能被占据。绝缘体的价带已被填满，而且带隙宽度很大，需要很大能量来使得电子越过带隙进入传导带成为传导电子，所以电导率很低。导体的能带只被填补了一部分，而且价带与传导带之间没有距离，在价带的电子可以自由移动，所以具有很高的电导率。量子自由电子理论无法给出带隙机制，因此每种固体都应该是很好的导体。能带理论也能对半导体给出合理解释。

应用泡利不相容原理，量子自由电子理论与能带理论关键性地奠定了凝聚态物理学的基础。凝聚态物质的很多种机械、电磁、光学、化学性质都是泡利不相容原理的直接后果。

重子的组成

重子Δ 是由三个上夸克uuu组成，假若Δ 的自旋磁量子数为3/2，则这三个上夸克的自旋都必须指向同样方向，因此引发了一个严峻问题，即这三个上夸克拥有同样的量子态，但是夸克是费米子，遵守泡利不相容原理，不能拥有同样的量子态。物理学者格林柏格因此提出，夸克具有色荷性质，夸克的颜色可以呈“红色”、“绿色”或“蓝色”三种中任意一种。这样，三个上夸克不再拥有同样的量子态。由于添加了色荷性质，重子的反对称性波函数 ψ ψ --> {\displaystyle \psi } 可以按照空间、自旋、味荷、色荷顺序分别表示为四个部分：

只考虑基态，则由于角量子数为零，空间部分 ψ ψ --> s p a c e {\displaystyle \psi _{space}} 具有对称性，可以被忽略。另外，所有至今发现的重子都是色单态（singlet），具有反对称性，色波函数 ψ ψ --> c o l o r {\displaystyle \psi _{color}} 为

其中， r {\displaystyle r} 、 g {\displaystyle g} 、 b {\displaystyle b} 分别标纪红波函数、绿波函数、蓝波函数。

所以，实际而言，只需要考虑自旋波函数 ψ ψ --> s p i n {\displaystyle \psi _{spin}} 与味波函数 ψ ψ --> f l a v o r {\displaystyle \psi _{flavor}} ：

函数 ψ ψ --> ′ {\displaystyle \psi "} 必须具有对称性。假若 ψ ψ --> s p i n {\displaystyle \psi _{spin}} 具有对称性，则 ψ ψ --> f l a v o r {\displaystyle \psi _{flavor}} 也具有对称性；反之亦然。假若 ψ ψ --> s p i n {\displaystyle \psi _{spin}} 具有反对称性，则 ψ ψ --> f l a v o r {\displaystyle \psi _{flavor}} 也具有反对称性；反之亦然。

例如，总自旋磁量子数 m j {\displaystyle m_{j}} 分别为3/2、1/2的Δ 粒子，其自旋波函数与味波函数为

参阅

钱德拉塞卡极限

洪德最大多重度规则

全同粒子

费米-狄拉克统计

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。