高线与垂心

任意一个三角形的三条高线交于一点，称为该三角形的垂心。证明如下：

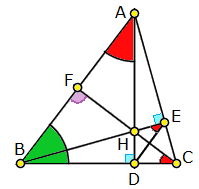
设有三角形ABC。过顶点A做BC的高线交BC于点D，过顶点B做AC的高线交AC于点E；直线AD和BE交于点H（如右图）。只需证明直线CH垂直于AB，就证明了CH是过C点的高线，即三条高线相交于一点H。因为欧氏几何中，给定一点与一直线，只存在一条直线过这个定点并与给定的直线垂直。

下证CH垂直于AB。设CH和AB的交点为F。由于角AEB和角ADB（右图中蓝色角）都是直角，A、B、D、E四点共圆，同理，C、D、H、E四点共圆。所以角DCH等于角DEH，角DEH等于角DEB等于角DAB（红色角相等）。

然而角DAB与角ABD（绿色角）的和是90度，所以角DCH与角ABD的和也是90度，即角FCB与角FBC的和是90度。因此三角形BCF是直角三角形，角BFC（紫色角）是直角。也就是说CH垂直于AB。因此三角形的三条高线交于一点H。证毕。

垂心坐标为(|x2x3+y2y31y1x3x1+y3y11y2x1x2+y1y21y3||x1y11x2y21x3y31|,|x2x3+y2y3x11x3x1+y3y1x21x1x2+y1y2x31||x1y11x2y21x3y31|){\displaystyle ({\frac {\begin{vmatrix}x_{2}x_{3}+y_{2}y_{3}&1&y_{1}\\x_{3}x_{1}+y_{3}y_{1}&1&y_{2}\\x_{1}x_{2}+y_{1}y_{2}&1&y_{3}\end{vmatrix}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}},{\frac {\begin{vmatrix}x_{2}x_{3}+y_{2}y_{3}&x_{1}&1\\x_{3}x_{1}+y_{3}y_{1}&x_{2}&1\\x_{1}x_{2}+y_{1}y_{2}&x_{3}&1\end{vmatrix}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}})}

性质

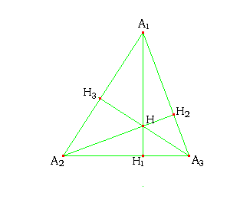
三条高线交于垂心

三角形的高可以用来计算其面积：三角形的面积S 等于过一个顶点的高乘以对边的长度再除以2： S=aha2{\displaystyle S={\frac {ah_{a}}{2}}}

其中a 为某一条边的边长，ha 为所对的顶点的高。

如果三角形ABC是等腰三角形，AB=AC，那么过A点的高线与过A点的中线和角平分线重合。

直角三角形的垂心是斜边所对的顶点。如果三角形ABC是直角三角形，其中角ACB是直角，那么过A点的高线是AC，过B点的高线是BC。三角形的垂心就是点C。

锐角三角形的垂心在三角形内部；钝角三角形的垂心在三角形外部。

欧拉定理断言，三角形的重心G、外心O 和垂心H 共线（称为欧拉线），并且重心是连接外心和垂心的线段的一个三等分点：HG =2GO

垂心将高线分成的两段的乘积相等：如右图中，A1H× × -->HH1=A2H× × -->HH2=A3H× × -->HH3{\displaystyle A_{1}H\times HH_{1}=A_{2}H\times HH_{2}=A_{3}H\times HH_{3}}

三角形的垂心到一边的距离，等于这边上的高线的延长线从垂足到外接圆的长度。

外心O 和垂心H 为等角共轭点。

三角形的三个垂足都在九点圆的圆周上。每个顶点和垂心所连成的线段的中点也在九点圆上。实际上，九点圆的九个点就是三边的中点和以上的六个点。九点圆的圆心也在欧拉线上，并且在垂心到外心的线段的中点。此外九点圆平分垂心与外接圆上的任一点的连线。

一个三角形ABC的三个顶点A、B、C和它的垂心H构成一个垂心组： A、B、C、H。也就是说，这四点中任意的三点的垂心都是第四点。

垂心的垂足三角形

三角形abc 是三角形ABC 的垂心的垂足三角形，它的内心正是ABC的垂心H.

过平面上一点P 分别做垂直于三角形每条边的垂线，与这条边相交于一点（垂足）。这三个点连成的三角形称为点P 的垂足三角形。垂心H 的垂足三角形是H1H2H3{\displaystyle H_{1}H_{2}H_{3}}。H 是三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}的内心，而三角形A1A2A3{\displaystyle A_{1}A_{2}A_{3}}的三个顶点是三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}的三个旁心。

锐角三角形A1A2A3{\displaystyle A_{1}A_{2}A_{3}}的所有内接三角形中，有最小周长的是垂心H 的垂足三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}。如果一束光从三角形的某一个高线垂足H1{\displaystyle H_{1}}、H2{\displaystyle H_{2}}或H3{\displaystyle H_{3}}出发沿着三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}的边的方向射出，那么它的光路将是闭合的，也就是三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}。这个性质仅对于垂心的垂足三角形成立：如果从三角形某一边某一点出发的光线经过反射能形成一个三角形的闭合光路，那么这个光路必然是三角形H1H2H3{\displaystyle H_{1}H_{2}H_{3}}。

垂心H 的垂足三角形的各个边分别平行于三角形的外接圆在各个顶点处的切线。

在三角形A1A2A3{\displaystyle A_{1}A_{2}A_{3}}中，三角形A1H2H3{\displaystyle A_{1}H_{2}H_{3}}、三角形H1A2H3{\displaystyle H_{1}A_{2}H_{3}}和三角形H1H2A3{\displaystyle H_{1}H_{2}A_{3}}的外接圆交于一点，这点就是A1A2A3{\displaystyle A_{1}A_{2}A_{3}}的垂心H。

高线的长度

过三角形某一顶点的高线的长度称为过这点的高或这一点上的高。三角形ABC的三个顶点A、B、C上的高通常分别记作ha{\displaystyle h_{a}}、hb{\displaystyle h_{b}}、hc{\displaystyle h_{c}}。它们可以用三角形三边的边长a、b、c（分别是顶点A、B、C的对边：BC、CA和AB的长度）来表示：

其中s是三角形的半周长：2s=a+b+c{\displaystyle 2s=a+b+c}。这三个关系式可以通过海伦公式：

以及三角形的面积公式：S=aha2{\displaystyle S={\frac {ah_{a}}{2}}}推出来。

高与内切圆半径

三角形内切圆的半径r与三个顶点上的高ha{\displaystyle h_{a}}、hb{\displaystyle h_{b}}、hc{\displaystyle h_{c}}有如下的关系：

而三角形的三个旁切圆的半径也和高有类似的关系：

其中的ra{\displaystyle r_{a}}、rb{\displaystyle r_{b}}、rc{\displaystyle r_{c}}分别指圆心在三个顶点A、B、C射出的内角平分线上的旁切圆Ja{\displaystyle J_{a}}、Jb{\displaystyle J_{b}}、Jc{\displaystyle J_{c}}的半径。

反海龙公式

如果设hs=(ha− − -->1+hb− − -->1+hc− − -->1)/2{\displaystyle h_{s}=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2}，那么有以下类似于海龙公式的三角形面积公式：

参见

垂心组

垂足三角形

垂直

九点圆

参考来源

R.A.约翰逊，单墫 译. 《近代欧氏几何学》. 上海教育出版社. ISBN 7-5320-6392-5. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。