解析几何中的垂直

在笛卡儿坐标系中，两条被如下等式所表示的直线 L {\displaystyle L} 和 M {\displaystyle M}

那么垂直的情况有两种：

只要没有一条是竖直（斜率=∞）的，那么 a {\displaystyle a} 和 c {\displaystyle c} 就是这两条直线的斜率。当且仅当直线 ( D 1 ) {\displaystyle ({\mathcal {D}}_{1})} 和 ( D 2 ) {\displaystyle ({\mathcal {D}}_{2})} 的斜率的积为 -1 时，即 a c = − − --> 1 {\displaystyle ac=-1} 时，这两条直线在这个平面垂直。

除此之外，若有一条直线是竖直的，那么另一条直线与它垂直当且仅当其斜率为 0 。

如果两条直线的表达式为：

那么只有一种情况：两条直线在这个平面相互垂直当且仅当 a 1 a 2 + b 1 b 2 = 0 {\displaystyle a_{1}a_{2}+b_{1}b_{2}=0}

假如用 V 1 = ( a 1 , b 1 ) {\displaystyle V_{1}=(a_{1},b_{1})} 和 V 2 = ( a 2 , b 2 ) {\displaystyle V_{2}=(a_{2},b_{2})} 来表示两条直线的方向向量，那么上面垂直的充分必要条件就是两个方向向量正交的充分必要条件。这说明了垂直实际上是正交关系（在二维和三维空间）的一个特例。

空间几何中的垂直

三维空间中不仅有直线与直线的垂直，也有直线与平面、平面与平面的垂直。

直线与直线的垂直 ：在三维空间中，判断两条直线之间的垂直关系比在平面上要困难。过其中一条直线作平行于另一条直线的平面，将另一条直线投影到这个平面上。如果这个投影与第一条直线垂直，那么就说两条直线垂直。

直线与平面的垂直 ：一条直线与一个平面垂直当且仅当它与平面中的每一条直线都垂直。一个等价的说法是两者垂直当且仅当直线平行于平面的法向量。

平面与平面的垂直 ：两个平面相互垂直当且仅当它们的法向量相互垂直。一个更几何的方法是看两个平面的交线（如果没有说明两平面平行）。选择一个平面，过两平面交线上的一点作一条垂直于交线并在平面中的直线，如果这条直线与另一个平面垂直，那么两平面垂直。

垂线的作图

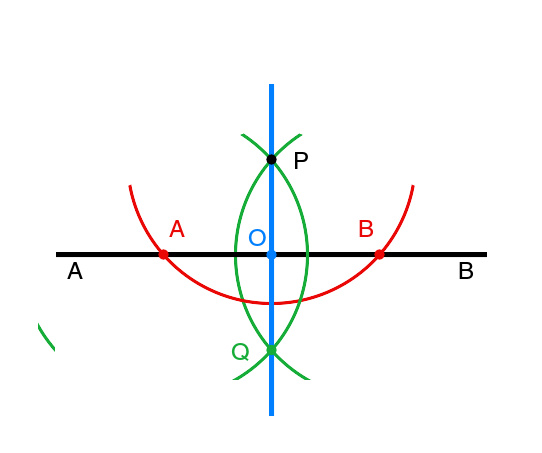
图二　过点P与直线AB相互垂直的构造过程

用尺规作一条过点P与直线AB相互垂直的直线，过程如下（见图二）：

步骤一（红色）：以点P为圆心作一个圆交直线AB于点A"和B"，点A"和B"与点P等距。

步骤二（绿色）：以点A"和B"为圆心，以PA"和PB"为半径作圆。令两圆的另一交点为Q。

步骤三（蓝色）：连接PQ以作出所求垂线。

为证明直线PQ与直线AB垂直，使用三角形SSS全等定理证明三角形QPA"和QPB"全等以求得三角形OPA"和OPB"也全等。然后使用三角形SAS全等定理证明角POA和POB相等。

参看

平行

投影

正交

参考来源

R.A.约翰逊 著，单壿 译. 近代欧氏几何学. 上海教育出版社. 1999. ISBN 7-532-06392-0 .

盛为民. 解析几何学. 浙江大学出版社. 2008. ISBN 7-308-06149-0 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。