概要

最简单的说，指数函数按恒定速率翻倍。例如细菌培养时细菌总数（近似的）每三个小时翻倍，和汽车的价值每年减少10%都可以被表示为一个指数。特别是复利，事实上就是它导致了雅各布·伯努利在1683年介入了现在叫做 e 的数：

后来约翰·伯努利在1697年研究了指数函数的微积分。

设 1 份借贷有 x 利率，逐月复利话，则每月增加当前值的 x/12 倍，每月总值都要乘以 (1+x/12)，一年的总值为 (1+x/12)，逐日复利的话，就是 (1+x/365)。设年中时段数可为无限，则有如下最初由欧拉提出的指数函数定义：

指数函数有基本的指数恒等式，

这是它写为 e 的原因。

在雅各布·伯努利之前，约翰·纳皮尔在1614年以及Jost Bürgi在6年后，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数，当时还没出现有理数幂的概念，直到1742年William Jones才发表了现在的幂指数概念。按后世的观点，Jost Bürgi的底数1.0001相当接近自然对数的底数 e，而约翰·纳皮尔的底数0.9999999相当接近 1e{\displaystyle {\frac {1}{e}}}。实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，Henry Briggs（英语：Henry Briggs (mathematician)）建议纳皮尔改用10为底数未果，他用自己的方法于1624年部分完成了常用对数表的编制。

形式定义

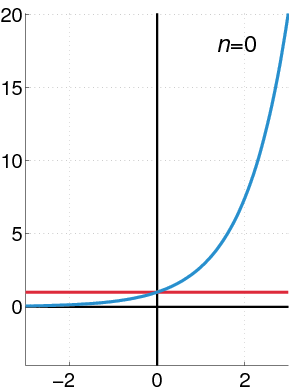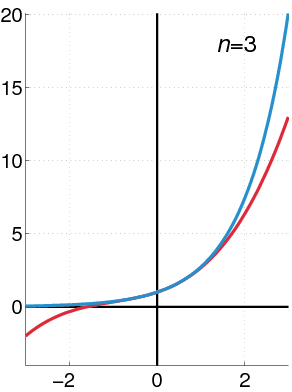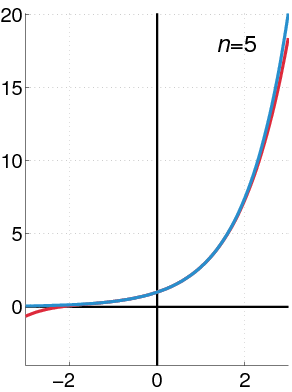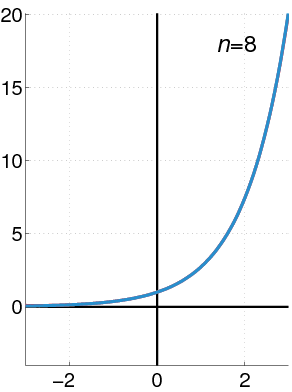
指数函数（蓝色），幂级数的前n+1项的和（红色）。

指数函数e可以用各种等价的方式定义。特别是它可以定义为幂级数：

或序列的极限：

在这些定义中，n!表示n的阶乘，而x可以是任何实数、复数、和巴拿赫代数的元素。

设 x≥ ≥ -->0{\displaystyle x\geq 0} 是确定的非负实数。定义

据二项式定理，

（设 x ≥ 0 得到最终的不等式）故此

可证明当 n 趋于无穷大时上述二定义等价。这些定义的进一步解释和它们的等价性的证明，参见文章指数函数的特征描述（英语：Characterizations of the exponential function）。

性质

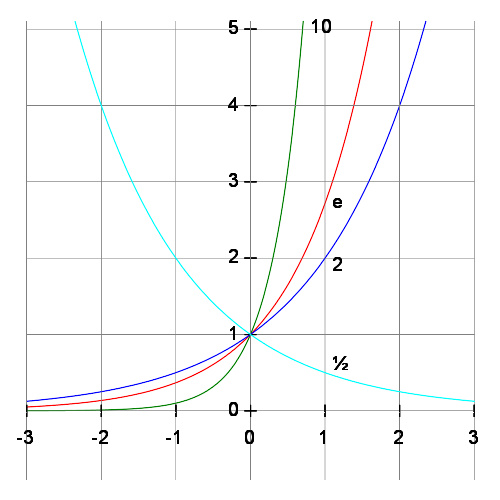
y = b对各种底数b的图像，分别为绿色的10、红色的e、蓝色的2和青色的1/2。

从指数函数的定义：

可得出它有幂运算的“指数定律”：

它们对所有实数x与y都是有效的。

因为在指数函数的定义中 x 是实数，可以使用自然对数，把更一般的指数函数，即正实数的实数幂函数定义为

定义于所有的b > 0，和所有的实数x。它叫做“底数为b的指数函数”。从而拓展了通过方根和方根运算定义的正有理数有理数幂函数：

而方根运算可通过自然对数和指数函数来表示

介入数e的根本动机，特别是在微积分中，是通过指数函数和对数来进行导数和积分运算。 一般指数函数 y = b 有极限形式的导数:

最右端的极限无关于变量 x：它依赖于底数 b 而是常量。根据求导的链式法则：

当这个底数是e时，这个常量等于1，因此有:

导数和微分方程

指数函数的导数等于这个函数的值。从在蓝色曲线上任意一点 P{\displaystyle P}，绘制红色切线，和高度为 h{\displaystyle h} 的垂直竖线，与在 x{\displaystyle x} 轴上的底边 b{\displaystyle b} 形成了一个直角三角形。因为在 P{\displaystyle P} 上的红色切线的斜率（导数）等于这个三角形的高度与底边长度的比，而导数等于这个函数的值，h{\displaystyle h} 必须等于 h{\displaystyle h} 与 b{\displaystyle b} 之比。因此底边 b{\displaystyle b} 必须总是 1{\displaystyle 1}。

指数函数在数学和科学中的重要性主要源于它的导数的性质。特别是

就是说，e是它自己的导数。这可以用泰勒级数证明：

对于常数K的形如Ke的函数是唯一有这个性质的函数（这得出自皮卡-林德洛夫定理）。其他等价说法有：

函数的图像的在任何一点上的斜率是这个函数在这一点上的高度。

函数在x的增长速率等于在这个函数在x上的值。

这个函数是微分方程y′=y{\displaystyle y"=y}的解。

exp是泛函导数的不动点。

事实上，很多不同的方程引发指数函数，包括薛定谔方程和拉普拉斯方程和简单谐波运动的方程。

对于有其他底数的指数函数：

所以任何指数函数都是它自己导数的常数倍。

如果一个变量的增长或衰减速率是与它的大小成比例的，比如在无限制情况下的人口增长、复利和放射性衰变，则这个变量可以写为常数倍的时间的指数函数。

进一步的，对任何可微函数f(x)，我们可以通过链式法则找到：

e的连分数

通过欧拉连分数公式得到e的连分数：

e的广义连分数收敛更快速:

或者，替换 z = ⁄y:

有特殊情况 z = 2:

在复平面上

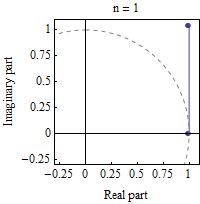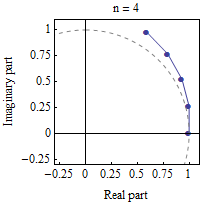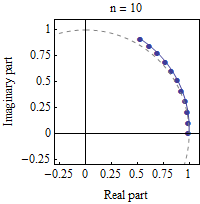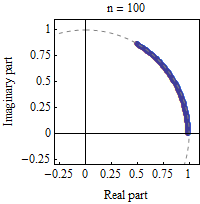
指数函数e可以定义为(1 + z/n)在n趋于无穷时的极限。在本动画中，z=iπ/3而n选取从1增到100的各种值。(1 + z/n)的计算显示为在复平面上n次乘法的组合效果。随着n变大，这些点趋近于复平面单位圆，覆及π/3弧度的角度。

如同在实数情况下，在复平面的指数函数可以用多种等价方式定义。比如幂级数形式的:

或者序列的极限：

它带有虚数周期2π π -->i{\displaystyle 2\pi i}，它可以写为

这里的a和b是实数值。参见欧拉公式，这个公式把指数函数和三角函数与双曲函数联系起来了。

在考虑定义在复平面上的函数的时候，指数函数拥有重要的性质

ez+w=ezew{\displaystyle \!\,e^{z+w}=e^{z}e^{w}}

e0=1{\displaystyle \!\,e^{0}=1}

ez≠ ≠ -->0{\displaystyle \!\,e^{z}\neq 0}

ddzez=ez{\displaystyle \!\,{d \over dz}e^{z}=e^{z}}

(ez)n=enz,n∈ ∈ -->Z{\displaystyle \,(e^{z})^{n}=e^{nz},n\in \mathbb {Z} }

对于所有的z和w。

它是周期的全纯函数。我们看到除了多项式的所有初等函数都以某种方式起源于指数函数。

扩展自然对数到复平面上的多值函数ln(z)，我们可以接着定义更一般性的指数函数：

对于所有复数z和w，这也是多值函数，即使是在z为实数的情况下。前面关于正实数情况下的指数乘积规则在多值函数情况下必须改为:

指数函数把在复平面上任何直线映射到在复平面中以原点为中心的对数螺线。要注意两个特殊情况：当最初的线平行于实轴的时候，结果的螺线永不遮盖（close in on）自身；当最初的线平行于虚轴的时候，结果的螺线是某个半径的圆。

在复平面上指数函数（主支）

z = Re(e)

z = Im(e)

矩阵和巴拿赫代数

上面给出的指数函数的定义可以用于所有巴拿赫代数，特别是对于方块矩阵（在这种情况函数叫做矩阵指数）。在这种情况下我们有

在非交换巴拿赫代数的上下文中，比如矩阵代数或在巴拿赫空间或希尔伯特空间上的算子，指数函数经常被认做实数参数的函数：

这里的A是这个代数的固定元素而t是任何实数。这个函数有重要的性质

在李代数上

从李代数到李群的“指数映射”有着上述性质。事实上因为R是带有乘法的所有正实数的李群的李代数，实数参数的常规指数函数是李代数下的特殊情况。类似的，因为所有方块实数矩阵的李代数M (n, R)属于所有正可逆方块矩阵的李群，方块矩阵的指数函数是李代数指数映射的特殊情况。

注释与引用

证明

参见

指数函数的特征描述

指数增长、指数衰减

对数

幂与幂定律

迭代幂次

古德温 - 斯塔顿积分

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。