历史

1935年，在普林斯顿高等研究院，爱因斯坦、博士后罗森、研究员波多尔斯基合作完成论文《物理实在的量子力学描述能否被认为是完备的？》，并且将这篇论文发表于5月份的《物理评论》 。这是最早探讨量子力学理论对于强关联系统所做的反直觉预测的一篇论文。在这篇论文里，他们详细表述EPR佯谬，试图借着一个思想实验来论述量子力学的不完备性质 。他们并没有更进一步研究量子纠缠的特性。

薛定谔阅读完毕EPR论文之后，有很多心得感想，他用德文写了一封信给爱因斯坦，在这封信里，他最先使用了术语 Verschränkung （他自己将之翻译为“纠缠”），这是为了要形容在EPR思想实验里，两个暂时耦合的粒子，不再耦合之后彼此之间仍旧维持的关联 。不久之后，薛定谔发表了一篇重要论文，对于“量子纠缠”这术语给予定义，并且研究探索相关概念。薛定谔体会到这概念的重要性，他表明，量子纠缠不只是量子力学的某个很有意思的性质，而是量子力学的特征性质；量子纠缠在量子力学与经典思路之间做了一个完全切割 。如同爱因斯坦一样，薛定谔对于量子纠缠的概念并不满意，因为量子纠缠似乎违反在相对论中对于信息传递所设定的速度极限 。后来，爱因斯坦更讥讽量子纠缠为鬼魅般的超距作用 。

EPR论文很显然地引起了众多物理学者的兴趣，启发他们探讨量子力学的基础理论。但是除了这方面以外，物理学者认为这论题与现代量子力学并没有什么牵扯，在之后很长一段时间，物理学术界并没有特别重视这论题，也没有发现EPR论文可能有什么重大瑕疵 。EPR论文试图建立定域性隐变量理论来替代量子力学理论。1964年，约翰·贝尔提出论文表明，对于EPR思想实验，量子力学的预测明显地不同于定域性隐变量理论。概略而言，假若测量两个粒子分别沿着不同轴向的自旋，则量子力学得到的统计关联性结果比定域性隐变量理论要强很多，贝尔不等式定性地给出这差别，做实验应该可以侦测出这差别 。因此，物理学者做了很多检试贝尔不等式的实验。

1972年，约翰·克劳泽与史达特·弗利曼（Stuart Freedman）首先完成这种检试实验 。1982年，阿兰·阿斯佩的博士论文是以这种检试实验为题目 。他们得到的实验结果符合量子力学的预测，不符合定域性隐变量理论的预测，因此证实定域性隐变量理论不成立。但是，至今为止，每一个相关实验都存在有漏洞，这造成了实验的正确性遭到质疑，在作总结之前，还需要完成更多精确的实验 。

这些年来，众多的卓越研究结果促成了应用这些超强关联来传递信息的可能性，从而导致了量子密码学的成功发展，最著名的有查理斯·贝内特（Charles Bennett）与吉勒·布拉萨（Gilles Brassard）发明的BB84协议、阿图尔·艾克特（Artur Eckert）发明的E91协议。

基本概念

  EPR佯谬的思想实验： 假设一个零自旋中性π介子衰变成一个电子与一个正电子，这两个衰变产物各自朝着相反方向移动至区域A、B。由于量子纠缠，假若位于区域A的爱丽丝与位于区域B的鲍勃分别测量粒子沿着同样轴向的自旋，则爱丽丝会测得上旋若且为若鲍勃会测得下旋，爱丽丝会测得下旋若且为若鲍勃会测得上旋。

假设一个零自旋中性π介子衰变成一个电子与一个正电子 。这两个衰变产物各自朝着相反方向移动。电子移动到区域A，在那里的观察者“爱丽丝”会观测电子沿着某特定轴向的自旋；正电子移动到区域B，在那里的观察者“鲍勃”也会观测正电子沿着同样轴向的自旋。在测量之前，这两个纠缠粒子共同形成了零自旋的“纠缠态” | ψ ψ --> 〉 {\displaystyle \left|\psi \right\rangle } ，是两个直积态（product state）的叠狄拉克狄拉克标记表示为

其中， | ↑ ↑ --> 〉 {\displaystyle \left|\uparrow \right\rangle } 、 | ↓ ↓ --> 〉 {\displaystyle \left|\downarrow \right\rangle } 分别表示粒子的自旋为上旋或下旋。

在圆括弧内的第一项 | ↑ ↑ --> 〉 ⊗ ⊗ --> | ↓ ↓ --> 〉 {\displaystyle \left|\uparrow \right\rangle \otimes \left|\downarrow \right\rangle } 表明，电子的自旋为上旋当且仅当正电子的自旋为下旋；第二项 | ↓ ↓ --> 〉 ⊗ ⊗ --> | ↑ ↑ --> 〉 {\displaystyle \left|\downarrow \right\rangle \otimes \left|\uparrow \right\rangle } 表明，电子的自旋为下旋当且仅当正电子的自旋为上旋。两种状况叠加在一起，每一种状况都有可能发生，不能确定到底哪种状况会发生，因此，电子与正电子纠缠在一起，形成纠缠态。假若不做测量，则无法知道这两个粒子中任何一个粒子的自旋，根据哥本哈根诠释，这性质并不存在。这单态的两个粒子相互反关联，对于两个粒子的自旋分别做测量，假若电子的自旋为上旋，则正电子的自旋为下旋，反之亦然；假若电子的自旋下旋，则正电子自旋为上旋，反之亦然。量子力学不能预测到底是哪一组数值，但是量子力学可以预言，获得任何一组数值的概率为50% 。

爱丽丝测量电子的自旋，她可能会得到两种结果：上旋或下旋，假若她得到上旋，则根据哥本哈根诠释，纠缠态坍缩为第一个项目所代表的量子态 | ↑ ↑ --> 〉 ⊗ ⊗ --> | ↓ ↓ --> 〉 {\displaystyle \left|\uparrow \right\rangle \otimes \left|\downarrow \right\rangle } ，随后，鲍勃测量正电子的自旋，他会得到下旋的概率为100%；类似地，假若爱丽丝测量的结果为下旋，则纠缠态坍缩为第二个项目所代表的量子态 | ↓ ↓ --> 〉 ⊗ ⊗ --> | ↑ ↑ --> 〉 {\displaystyle \left|\downarrow \right\rangle \otimes \left|\uparrow \right\rangle } ，随后鲍勃会测量得到上旋。

设想一个类比的经典统计学实验，将一枚硬币沿着圆周切成两半，每一半币不是头币就是尾币，将这两枚半币分别置入两个信封，然后随机交给爱丽丝与鲍勃。假若爱丽丝打开信封，查看她得到的是哪种硬币，她将无法预测这结果，因为得到头币或尾币的概率各为50%。鲍勃也会遇到同样的状况。可以确定的是，假若爱丽丝得到头币，则鲍勃会得到尾币；假若爱丽丝得到尾币，则鲍勃会得到头币。这两个事件完全地反关联 。

在先前的量子纠缠实验里，爱丽丝与鲍勃分别测量粒子沿着同样轴向的自旋，虽然这涉及到量子关联，他们仍旧会得到与经典关联实验同样的结果。怎样区分量子关联与经典关联？假若爱丽丝与鲍勃分别测量粒子沿着不同轴向的自旋，而不是沿着同样轴向，然后检验实验数据是否遵守贝尔不等式，则他们会发觉，量子纠缠系统必定违反贝尔不等式，而经典物理系统必定遵守贝尔不等式。因此，贝尔不等式乃是一种很灵敏的侦测量子纠缠的工具。量子纠缠实验所涉及的量子关联现象无法用经典统计物理学概念来解释，在经典统计物理学里，找不到类似案例 。

粒子沿着不同轴向的自旋彼此之间是不相容可观察量，对于这些不相容可观察量作测量必定不能同时得到明确结果，这是量子力学的一个基础理论。在经典力学里，这基础理论毫无意义，理论而言，任何粒子性质都可以被测量至任意准确度。贝尔定理意味着一个事实，一个已被实验检试的事实，即对两个不相容可观察量做测量得到的结果不遵守贝尔不等式 。因此，基础而言，量子纠缠是个非经典现象。

不确定性原理的维持必须倚赖量子纠缠机制。例如，设想先前的一个零自旋中性π介子衰变案例，两个衰变产物各自朝着相反方向移动，现在分别测量电子的位置与正电子的动量，假若量子纠缠机制不存在，则可借着守恒定律预测两个粒子各自的位置与动量，这违反了不确定性原理。由于量子纠缠机制，粒子的位置与动量遵守不确定性原理。

从以相对论性速度移动的两个参考系分别测量两个纠缠粒子的物理性质，尽管在每一个参考系，测量两个粒子的时间顺序不同，获得的实验数据仍旧违反贝尔不等式，仍旧能够可靠地复制出两个纠缠粒子的量子关联 。

数学表述

以下各小节是为那些具有量子力学正式的数学描述的一个良好的工作知识的读者而写，包括文章推导中熟悉的形式和理论框架：狄拉克符号(BRA-KET符号)和量子力学的数学表述。本章节涉及到密度算符概念，若不熟悉密度算符相关概念，请先阅读条目密度算符。

严格定义

假设一个复合系统是由两个子系统A、B所组成 ，这两个子系统A、B的希尔伯特空间分别为 H A {\displaystyle H_{A}} 、 H B {\displaystyle H_{B}} ，则复合系统的希尔伯特空间 H A B {\displaystyle H_{AB}} 为张量积

设定子系统A、B的量子态分别为 | α α --> 〉 〉 --> A {\displaystyle |\alpha \rangle _{A}} 、 | β β --> 〉 〉 --> B {\displaystyle |\beta \rangle _{B}} ，假若复合系统的量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 不能写为张量积 | α α --> 〉 〉 --> A ⊗ ⊗ --> | β β --> 〉 〉 --> B {\displaystyle |\alpha \rangle _{A}\otimes |\beta \rangle _{B}} ，则称这复合系统为子系统A、B的纠缠系统，两个子系统A、B相互纠缠。

纯态

假设一个复合系统是由两个不相互作用的子系统A、B所组成，子系统A、B的量子态分别为 | α α --> 〉 〉 --> A {\displaystyle |\alpha \rangle _{A}} 、 | β β --> 〉 〉 --> B {\displaystyle |\beta \rangle _{B}} ，则复合系统的量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 为

这种形式的量子态称为直积态（product state）。量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 具有可分性（separability），是“可分态”。对于子系统A做测量，必定不会影响到子系统B；反之亦然。因此，对于这种复合系统，测量任意子系统的可观察量时，不必考虑到另外一个子系统。

假设子系统A、B相互耦合，则复合系统的量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 不能用单独一项直积态表示，必须用多项直积态的量子叠加表示。量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 不具有可分性，是“纠缠态”。假设 { | a i 〉 〉 --> A } {\displaystyle \{|a_{i}\rangle _{A}\}} 、 { | b j 〉 〉 --> B } {\displaystyle \{|b_{j}\rangle _{B}\}} 分别为希尔伯特空间 H A {\displaystyle H_{A}} 、 H B {\displaystyle H_{B}} 的规范正交基。在希尔伯特空间 H A ⊗ ⊗ --> H B {\displaystyle H_{A}\otimes H_{B}} 里，这复合系统的量子态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} 可以表示为

其中， c i j {\displaystyle c_{ij}} 是复系数。

例如，假设 | 0 〉 〉 --> A {\displaystyle |0\rangle _{A}} 、 | 1 〉 〉 --> A {\displaystyle |1\rangle _{A}} 分别为规范正交基 { | a i 〉 〉 --> A } {\displaystyle \{|a_{i}\rangle _{A}\}} 的基底矢量， | 0 〉 〉 --> B {\displaystyle |0\rangle _{B}} 、 | 1 〉 〉 --> B {\displaystyle |1\rangle _{B}} 分别为规范正交基 { | b j 〉 〉 --> B } {\displaystyle \{|b_{j}\rangle _{B}\}} 的基底矢量。以下形式的量子态是一个纠缠态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} ：

现在假设爱丽丝、鲍勃分别是子系统A、B的观察者，规范正交基 { | a i 〉 〉 --> A } {\displaystyle \{|a_{i}\rangle _{A}\}} 的基底矢量 | 0 〉 〉 --> A {\displaystyle |0\rangle _{A}} 、 | 1 〉 〉 --> A {\displaystyle |1\rangle _{A}} 为可观察量 O A {\displaystyle O_{A}} 的本征态矢量，对应的本征值分别为 0 {\displaystyle 0} 、 1 {\displaystyle 1} 。规范正交基 { | b j 〉 〉 --> B } {\displaystyle \{|b_{j}\rangle _{B}\}} 的基底矢量 | 0 〉 〉 --> B {\displaystyle |0\rangle _{B}} 、 | 1 〉 〉 --> B {\displaystyle |1\rangle _{B}} 为可观察量 O B {\displaystyle O_{B}} 的本征态矢量，对应的本征值分别为 0 {\displaystyle 0} 、 1 {\displaystyle 1} 。假设爱丽丝测量可观察量 O A {\displaystyle O_{A}} ，则结果可能有两种结果，每一种结果发生的概率相同，都是50%：

爱丽丝测量可观察量 O A {\displaystyle O_{A}} 的结果为0，量子态坍缩为 | 0 〉 〉 --> A | 1 〉 〉 --> B {\displaystyle |0\rangle _{A}|1\rangle _{B}} ，那么，鲍勃在之后测量可观察量 O B {\displaystyle O_{B}} 的结果为1。

爱丽丝测量可观察量 O A {\displaystyle O_{A}} 的结果为1，量子态坍缩为 | 1 〉 〉 --> A | 0 〉 〉 --> B {\displaystyle |1\rangle _{A}|0\rangle _{B}} ，那么，鲍勃在之后测量可观察量 O B {\displaystyle O_{B}} 的结果为0。

由此可见，爱丽丝对子系统A测量可观察量 O A {\displaystyle O_{A}} 这定域动作改变了子系统B，尽管子系统A、B之间可能相隔很长一段距离，这就是两个子系统量子纠缠的现象。更详尽内容，请参阅EPR佯谬。

由于爱丽丝测量得到的结果具有随机性，爱丽丝不知道复合系统会怎样坍缩，她不能够以超光速传递这信息给鲍勃，因此，没有违反因果性（causality）。更详尽内容，请参阅不可通讯定理（no-communication theorem）。

混合态

混合态是由几种纯态依照统计概率组成的量子态。假设一个量子系统处于纯态 | ψ ψ --> 1 〉 〉 --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 〉 〉 --> {\displaystyle |\psi _{2}\rangle } 、 | ψ ψ --> 3 〉 〉 --> {\displaystyle |\psi _{3}\rangle } 、……的概率分别为 w 1 {\displaystyle w_{1}} 、 w 2 {\displaystyle w_{2}} 、 w 3 {\displaystyle w_{3}} 、……，则这混合态量子系统的密度算符 ρ ρ --> {\displaystyle \rho } 定义为

注意到所有概率的总和为1：

将先前对于纯态的可分性所做的定义加以延伸，具有可分性的两体混合态，其密度算符可以写为

其中， w i {\displaystyle w_{i}} 是正实值系数，可以诠释为概率， ρ ρ --> i , A {\displaystyle \rho _{i,A}} 是子系统A的一组密度算符， ρ ρ --> i , B {\displaystyle \rho _{i,B}} 是子系统B的一组密度算符。

假若两体混合态可以以上述方程表示，则这混合态具有可分性，其量子系统遵守贝尔不等式，不被量子纠缠；否则，这混合态具有不可分性，是纠缠态，其量子系统被量子纠缠，但并不一定会违反贝尔不等式 。

一般而言，很不容易辨识任意混合态量子系统到底是否被量子纠缠。一般两体案例已被证明为困难 。对于 2 × × --> 2 {\displaystyle 2\times 2} 与 2 × × --> 3 {\displaystyle 2\times 3} 案例，佩雷斯-霍罗德基判据（Peres-Horodecki criterion）是可分性的充要条件 。

怎样做实验制成混合态？试想非偏振态光子是怎样制成的。一种方法是利用处于动力学平衡的系统，这系统拥有很多个微观态（microstate），伴随每一个微观态都有其发生的概率（玻尔兹曼因子），它们会因热力学涨落（thermal fluctuation）从一个微观态变换到另一个微观态。热力学随机性可以解释白炽灯怎样发射非偏振光子。另一种方法是引入不确定性于系统的制备程序，例如，将光束通过表面粗糙的双折射晶体，使得光束的不同部分获得不同偏振。第三种方法应用EPR机制，有些放射性衰变会发射两个光子朝着反方向移动离开，这纠缠系统的量子态为 ( | R , L 〉 〉 --> + | L , R 〉 〉 --> ) / 2 {\displaystyle (|R,L\rangle +|L,R\rangle )/{\sqrt {2}}} ；其中， | R 〉 〉 --> {\displaystyle |R\rangle } 、 | L 〉 〉 --> {\displaystyle |L\rangle } 分别为右旋圆偏振态、左旋圆偏振态。整个系统是处于纯态，但是每一个光子子系统的物理行为如同非偏振态光子，从分析光子子系统的约化密度算符，可以得到这结论。

约化密度算符

约化密度算符的点子最先由保罗·狄拉克于1930年提出 。假设由两个子系统A、B所组成的复合系统，其量子态为纯态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ，其密度算符 ρ ρ --> {\displaystyle \rho } 为

这密度算符也是投影算符，能够将复合系统的希尔伯特空间 H A B {\displaystyle H_{AB}} 里的任意量子态 | ϕ ϕ --> 〉 〉 --> {\displaystyle |\phi \rangle } 投影到量子态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } ：

取密度算符 ρ ρ --> {\displaystyle \rho } 对于子系统B的偏迹数，可以得到子系统A的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} ：

例如，先前提到的纠缠态 | ψ ψ --> 〉 〉 --> A B = ( | 0 〉 〉 --> A ⊗ ⊗ --> | 1 〉 〉 --> B − − --> | 1 〉 〉 --> A ⊗ ⊗ --> | 0 〉 〉 --> B ) / 2 {\displaystyle |\psi \rangle _{AB}=(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B})/{\sqrt {2}}} ，其子系统A的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} 为

如同预想，这公式演示出，子系统A的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} 为混合态。

冯诺伊曼熵

在量子统计力学（quantum statistical mechanics）里，冯诺伊曼熵（von Neumann entropy）是经典统计力学关于熵概念的延伸。对于密度矩阵为 ϱ ϱ --> {\displaystyle \varrho } 的混合态，冯诺伊曼熵定义为

这公式涉及到矩阵对数（logarithm of a matrix），似乎很难计算 ，但密度算符 ρ ρ --> {\displaystyle \rho } 是自伴算符，具有谱表示

其中， | a i 〉 〉 --> {\displaystyle |a_{i}\rangle } 是本征值为 a i {\displaystyle a_{i}} 的本征态，所有 | a i 〉 〉 --> {\displaystyle |a_{i}\rangle } 形成一个规范正交基。

因此，可以将密度算符 ρ ρ --> {\displaystyle \rho } 的密度矩阵对角化，将冯诺伊曼熵更简单地以对角化后的密度矩阵 ϱ ϱ --> {\displaystyle \varrho } 定义为

其中， ϱ ϱ --> i i {\displaystyle \varrho _{ii}} 是密度矩阵 ρ ρ --> {\displaystyle \rho } 的第 i {\displaystyle i} 个对角元素。

冯诺伊曼熵 σ σ --> {\displaystyle \sigma } 又可以写为

从这形式可以推论冯诺伊曼熵与经典信息论里的夏农熵相关 。

在这里，视每一个本征值 a i {\displaystyle a_{i}} 为处于本征态 | a i 〉 〉 --> {\displaystyle |a_{i}\rangle } 的概率。假若某事件的发生概率为零，则这事件不应贡献出丝毫冯诺伊曼熵。从数学而言，以下极限为零：

因此，可以采用约定

纯态的冯诺伊曼熵为零，因为其对角化之后的密度矩阵，每一个对角元素 a i {\displaystyle a_{i}} 必定满足 a i = 0 {\displaystyle a_{i}=0} 或 ln ⁡ ⁡ --> a i = 0 {\displaystyle \ln a_{i}=0} 。

完全随机混合态的 N × × --> N {\displaystyle N\times N} 密度矩阵，其冯诺伊曼熵 σ σ --> {\displaystyle \sigma } 为

冯诺伊曼熵可以被视为量子系统失序现象的一种度量，纯态的冯诺伊曼熵最小，数值为 0 {\displaystyle 0} ，而完全随机混合态则的冯诺伊曼熵最大，数值为 ln ⁡ ⁡ --> N {\displaystyle \ln N} 。

量子纠缠度量

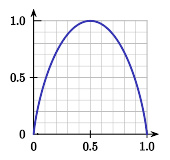
  对于两体纯态系统，纠缠度量 E ( ρ ρ --> ) {\displaystyle E(\rho )} （竖轴）与任意本征值 a i {\displaystyle a_{i}} （横轴）的关系曲线。当本征值为0.5时，纠缠度量最大，这纯态是最大纠缠态。

量子纠缠与量子系统失序现象、量子信息丧失程度密切相关。量子纠缠越大，则子系统越失序，量子信息丧失越多；反之，量子纠缠越小，子系统越有序，量子信息丧失越少。因此，冯诺伊曼熵可以用来定量地描述量子纠缠，另外，还有其它种度量也可以定量地描述量子纠缠。对于两体复合系统，这些纠缠度量较常遵守的几个规则为

纠缠度量必须映射从密度算符至正实数。

假若整个复合系统不处于纠缠态，则纠缠度量必须为零。

对于纯态复合系统，纠缠度量必需约化为冯诺伊曼熵。

对于命定性的定域运算与经典通讯（local operation and classical communication）变换，纠缠度量不会增加。

对于两体纯态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} ，根据施密特分解（Schimidt decomposition）

其中， σ σ --> A {\displaystyle \sigma _{A}} 、 σ σ --> B {\displaystyle \sigma _{B}} 分别为子系统A、B的冯诺伊曼熵， a i {\displaystyle a_{i}} 是先前提到的子系统A约化密度算符的几个本征值之一。

所以，整个复合系统的纠缠度量 E ( ρ ρ --> ) {\displaystyle E(\rho )} 可以设定为任意子系统A或B的冯诺伊曼熵：

对于两体纯态 | ψ ψ --> 〉 〉 --> A B {\displaystyle |\psi \rangle _{AB}} ，假若子系统的约化密度矩阵是对角矩阵

则这两体纯态具有最大可能的纠缠度量 E ( ρ ρ --> ) = ln ⁡ ⁡ --> N {\displaystyle E(\rho )=\ln N} ，但是它的子系统也完全失序，并且无法预测对于子系统做测量得到的结果，只能预测两个子系统之间的量子关联。

对于两体纯态，只有冯诺伊曼熵能够量度量子纠缠，因为只有它能够满足某些量度量子纠缠必须遵守的判据。对于混合态，使用冯诺伊曼熵并不是唯一能够量度量子纠缠的方法。

量子纠缠与不可分性

假设一个量子系统是由几个处于量子纠缠的子系统组成，而整体系统所具有的某种物理性质，子系统不能私自具有，这时，不能够对子系统给定这种物理性质，只能对整体系统给定这种物理性质，它具有“不可分性”。不可分性不一定与空间有关，处于同一区域的几个物理系统，只要彼此之间没有任何纠缠，则它们各自可拥有自己的物理性质。物理学者艾雪·佩雷斯（Asher Peres）给出不可分性的数学定义式，可以计算出整体系统到底具有可分性还是不可分性。假设整体系统具有不可分性，并且这不可分性与空间无关，则可将它的几个子系统分离至两个相隔遥远的区域，这动作凸显出不可分性与定域性的不同──虽然几个子系统分别处于两个相隔遥远的区域，仍旧不可将它们个别处理。在EPR佯谬里，由于两个粒子分别处于两个相隔遥远的区域，整体系统被认为具有可分性，但因量子纠缠，整体系统实际具有不可分性，整体系统所具有明确的自旋z分量，两个粒子各自都不具有 。

应用

量子纠缠是一种物理资源，如同时间、能量、动量等等，能够萃取与转换。应用量子纠缠的机制于量子信息学，很多平常不可行的事务都可以达成：

量子密钥分发能够使通信双方共同拥有一个随机、安全的密钥，来加密和解密信息，从而保证通信安全。在量子密钥分发机制里，给定两个处于量子纠缠的粒子，假设通信双方各自接受到其中一个粒子，由于测量其中任意一个粒子会摧毁这对粒子的量子纠缠，任何窃听动作都会被通信双方侦测发觉。

密集编码（superdense coding）应用量子纠缠机制来传送信息，每两个经典位元的信息，只需要用到一个量子位元，这科技可以使传送效率加倍。

量子隐形传态应用先前发送点与接收点分享的两个量子纠缠子系统与一些经典通讯技术来传送量子态或量子信息（编码为量子态）从发送点至相隔遥远距离的接收点 。

量子算法（quantum algorithm）的速度时常会胜过对应的经典算法很多。但是，在量子算法里，量子纠缠所扮演的角色，物理学者尚未达成共识。有些物理学者认为，量子纠缠对于量子算法的快速运算贡献很大，但是，只倚赖量子纠缠并无法达成快速运算 。

在量子计算机体系结构里，量子纠缠扮演了很重要的角色。例如，在一次性量子计算机（one-way quantum computer）的方法里，必须先制备出一个多体纠缠态，通常是图形态（graph state）或簇态（cluster state），然后借着一系列的测量来计算出结果。

不同种类的纠缠态

以下列出一些常遇到的纠缠态：

贝尔态（Bell state）有两个量子位元 | 〉 〉 --> A {\displaystyle |\ \rangle _{A}} 、 | 〉 〉 --> B {\displaystyle |\ \rangle _{B}} ：

这四个纯态都是最大纠缠态（根据冯诺伊曼熵计算），它们共同形成规范正交基在两个量子位元的希尔伯特空间里。贝尔定理主要使用贝尔态来做出重要论述。

GHZ态（GHZ state）的量子位元数 M {\displaystyle M} 大于2，以方程表示为

假若 M = 2 {\displaystyle M=2} ，这方程约化为贝尔态 | Φ Φ --> + 〉 〉 --> {\displaystyle |\Phi ^{+}\rangle } 的方程。通常，GHZ态的量子位元数为 M = 3 {\displaystyle M=3} ，三体种特别的三体系统。量子三元（qutrit）是量子位元的推广。量子三元的三个基态分别为 | 0 〉 〉 --> {\displaystyle |0\rangle } 、 | 1 〉 〉 --> {\displaystyle |1\rangle } 、 | 2 〉 〉 --> {\displaystyle |2\rangle } 。自旋为1的粒子，其自旋自由度有三，所对应的本征值为+1, 0, -1，此种粒子可用来制备量子三元。

NOON态（NOON state）是两个项目的量子叠加，一个项目是 N {\displaystyle N} 个粒子处于量子态 a {\displaystyle a} 与 0 {\displaystyle 0} 个粒子处于量子态 b {\displaystyle b} ，另一个项目是 0 {\displaystyle 0} 个粒子处于量子态 a {\displaystyle a} 与 N {\displaystyle N} 个粒子处于量子态 b {\displaystyle b} ：

在量子计量学（quantum metrology）里，光学干涉仪利用NOON态来准确地量度相位 。

纠缠系统的制备

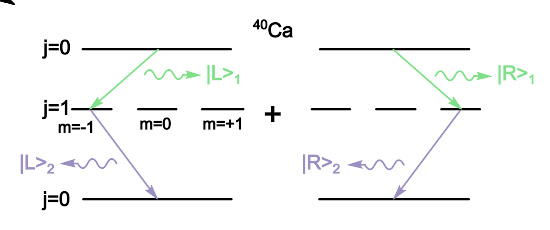
  Ca 激发态的两种衰变路径，其分别对应的两个量子态由于量子叠加，衰变过程中发射的两个光子被纠缠在一起。在此图中，淡绿色、淡蓝色波形线分别表示551.3nm波长与422.7nm波长的光子， j {\displaystyle j} 是总角量子数， m {\displaystyle m} 是磁量子数。

量子纠缠通常是因为亚原子粒子直接耦合而产生的。早期， 原子级联 （ 英语 ： Collision cascade ） 就是用来制备纠缠态的一种方法。例如，处于激发态的钙原子，会先后发射出两个光子，因此衰变至基态。假若第一个光子具有左旋圆偏振，则第二个光子具有左旋圆偏振；假若第一个光子具有右旋圆偏振，则第二个光子具有右旋圆偏振。假若不做测量，则不能知道到底哪个光子具有左旋圆偏振，哪个光子具有右旋圆偏振。因此这两个光子被纠缠在一起，纠缠态为分别描述这两种组合的两个直积态的叠加： ( | L 〉 〉 --> 1 | L 〉 〉 --> 2 + | R 〉 〉 --> 1 | R 〉 〉 --> 2 ) / 2 {\displaystyle (|L\rangle _{1}|L\rangle _{2}+|R\rangle _{1}|R\rangle _{2})/{\sqrt {2}}} ；其中， | L 〉 〉 --> {\displaystyle |L\rangle } 、 | R 〉 〉 --> {\displaystyle |R\rangle } 分别是左旋圆偏振态、右旋圆偏振态，下标 1 {\displaystyle 1} 、 2 {\displaystyle 2} 分别标示第一个、第二个光子 。

现今最常用的方法之一是自发参量下转换。这自发参量下转换方法的一种实现是照射激光束于偏硼酸钡晶体（beta-barium borate crystal，一种非线性晶体），大多数光子会穿透过晶体，只有少数光子，会因第二型自发参量下转换，生成一对一对的孪生光子。这些孪生光子对的直线轨道分别包含于两个圆锥面，如引言段落的绘图所示，一个圆锥面包含水平偏振轨道，另一个圆锥面包含垂直偏振轨道，而两个圆锥面的交集是两条直线，轨道为这两条直线的两个光子可以具有水平偏振或垂直偏振，假若一个具有水平偏振，则另一个具有垂直偏振；假若一个具有垂直偏振，则另一个具有水平偏振。假若不做测量，则不能知道到底哪个光子具有水平偏振，哪个光子具有垂直偏振，因此，这两个偏振相互垂直的光子纠缠在一起，纠缠态为 ( | H 〉 〉 --> 1 | V 〉 〉 --> 2 + | V 〉 〉 --> 1 | H 〉 〉 --> 2 ) / 2 {\displaystyle (|H\rangle _{1}|V\rangle _{2}+|V\rangle _{1}|H\rangle _{2})/{\sqrt {2}}} ；其中， | H 〉 〉 --> {\displaystyle |H\rangle } 是水平偏振， | V 〉 〉 --> {\displaystyle |V\rangle } 是垂直偏振 。

在凝聚态量子计算机里，最具有潜力的候选之一是量子点科技。量子点是一种半导体奈米晶体，能够束缚激子于微小三维空间内。激子是一对电子与空穴因静电库仑作用相互吸引而构成的束缚态。假若电子与空穴复合，造成激子衰变，过剩能量会以光子形式发射释出。在量子点里，也可能找到双激子（biexciton），这是由两个电子与两个空穴组成的束缚态。双激子会先发射一个光子，衰变成一个激子，然后再发射一个光子，衰变至基态。假若第一个光子具有水平偏振，则第二个光子也具有水平偏振，否则，两个光子都具有垂直偏振。这两种过程叠加而生成一对偏振纠缠的光子，其纠缠态为 ( | H 〉 〉 --> 1 | H 〉 〉 --> 2 + | V 〉 〉 --> 1 | V 〉 〉 --> 2 ) / 2 {\displaystyle (|H\rangle _{1}|H\rangle _{2}+|V\rangle _{1}|V\rangle _{2})/{\sqrt {2}}} 。

在 光学谐振腔 （ 英语 ： optical cavity ） 内，里德伯原子会因拉比振动发射或吸收光子的机制，应用这机制来交换光子，两个或三个里德伯原子可以形成纠缠态 。

几个囚禁在离子阱内的囚禁离子可以被纠缠在一起。给定离子的两个内态分别为基态 | g 〉 〉 --> {\displaystyle |g\rangle } 与激发态 | e 〉 〉 --> {\displaystyle |e\rangle } ，每一种内态都有其特定的内能。囚禁在谐振子位势内的离子会拥有离散的振动能级 n {\displaystyle n} 与对应的振动能态 | n 〉 〉 --> {\displaystyle |n\rangle } 。照射边带频率（sandband frequency） Ω Ω --> ± ± --> ω ω --> n {\displaystyle \Omega \pm \omega _{n}} 激光于离子，可以将内态与振动能级态纠缠在一起，纠缠态为 | g , n 〉 〉 --> + | e , n ± ± --> 1 〉 〉 --> {\displaystyle |g,n\rangle +|e,n\pm 1\rangle } ；其中， Ω Ω --> {\displaystyle \Omega } 是 | g 〉 〉 --> {\displaystyle |g\rangle } 与 | e 〉 〉 --> {\displaystyle |e\rangle } 之间的拉比频率， ω ω --> n {\displaystyle \omega _{n}} 是振动能级 n {\displaystyle n} 与 n ± ± --> 1 {\displaystyle n\pm 1} 之间的频率差 。

时间奥秘

亚瑟·爱丁顿认为，能量的缓慢散布是时间流向不可逆反的证据。但是，从基本的物理定律，并无法观测到时间流向；顺着时间流向或逆着时间流向，这些物理定律都能同样成立，这引起物理学者极大的困惑，他们只能从热力学的统计分布给出时间流向的理论论述。物理学者赛斯·劳埃德（Seth Lloyd）在1988年博士论文里猜想，量子纠缠是时间流向的源头；时间的流向是关联递加的方向，这机制源自于量子纠缠。起初，这点子并未受到学术界重视。后来，越来越多物理学者在这方面有所突破，他们发现了时间流向的更基础源头，微观粒子彼此相互作用产生量子纠缠，因此形成能量散布与平衡的现象，关于微观粒子的信息通过量子纠缠机制，从一至十、从十至百，逐步泄露到整个环境，因此显示出时间流向 。

有些物理学者主张，时间是一种从量子纠缠衍生出来的凸显现象 。于1960年代提出的惠勒－德维特方程尝试将量子力学与广义相对论连结在一起，但是，这方程并没有将时间纳入考量，因此引发了时间问题（problem of time）。直到1983年为止，这是学术界一大难题。在那年，档恩·佩吉（Don Page）与威廉·乌特斯（William Wooters）找到一个建基于量子纠缠现象的解答，说明怎样用量子纠缠来测量时间 。

2013年，意大利都灵的国立计量研究院（Istituto Nazionale di Ricerca Metrologica）实验团队完成实验检试佩吉与乌特斯的点子，证实这点子值得进一步研究 。

虫洞

  洛伦兹虫洞（史瓦西虫洞）的电脑绘图。

将两个黑洞纠缠在一起，然后再将它们分离，就可制成一个虫洞连结在它们之间 。将这论述加以延伸，物理学者质疑，虫洞的连结与量子纠缠的连结是同一种现象，只有系统的尺寸如同天壤之别 。

类似地从弦理论来检视，纠缠两个夸克也会有同样的作用 。

这些理论结果为一些新理论提供支持。这些新理论表明，引力与它的物理性质不是基础的，而是来自于量子纠缠。虽然量子力学正确地描述在微观层次的相互作用，它尚未能够解释引力。量子引力理论应该能够演示出经典引力不是基础的，就如同阿尔伯特·爱因斯坦所提议，而是从更基础的量子现象产生 。

施温格效应（Schwinger effect）从真空生成的纠缠粒子对，处于电场的作用下，可以被捕获，不让它们湮灭回真空。这些被捕获的粒子相互纠缠，可以映射到四维空间（一种时空的表现）。与之不同，物理学者认为，引力存在于第五维，按照爱因斯坦的定律，将时空弯曲与变形 。

根据全息原理（holographic principle），所有在第五维的事件可以变换为在其它四维的事件 ，因此，在纠缠粒子被生成的同时，虫洞也被生成。更基础地，这论述建议，引力与它弯曲时空的能力来自于量子纠缠 。

案例

以两颗向相反方向移动但速率相同的电子为例，即使一颗行至太阳边，一颗行至冥王星边，在如此遥远的距离下，它们仍保有关联性（correlation）；亦即当其中一颗被操作（例如量子测量）而状态发生变化，另一颗也会即时发生相应的状态变化。如此现象导致了鬼魅似的超距作用之猜疑，仿佛两颗电子拥有超光速的秘密通信一般，似与狭义相对论中所谓的定域性原理相违背。这也是当初阿尔伯特·爱因斯坦与同僚玻理斯·波多斯基、纳森·罗森于1935年提出的EPR佯谬来质疑量子力学完备性的理由。

具有量子纠缠的两颗电子——电子1和电子2，其自旋性质之纠缠态可以下面式子为例：

无法写成 | ψ ψ --> 〉 〉 --> 1 ⊗ ⊗ --> | ϕ ϕ --> 〉 〉 --> 2 {\displaystyle |\psi \rangle _{1}\otimes |\phi \rangle _{2}} ，即两个量子态的张量积。 下标1和2表示这是电子1和电子2的量子态，采取 | 0 〉 〉 --> {\displaystyle |0\rangle } 表示自旋的 z {\displaystyle z} 方向分量向上， | 1 〉 〉 --> {\displaystyle |1\rangle } 表示自旋的 z {\displaystyle z} 方向分量向下。

太阳边的科学家决定对电子1做投影式量子测量，其测到的随机性结果不是 | 0 〉 〉 --> {\displaystyle |0\rangle } 就是 | 1 〉 〉 --> {\displaystyle |1\rangle } 。当其测量结果显示为状态 | 0 〉 〉 --> {\displaystyle |0\rangle } ，则冥王星的科学家在此之后，或很近、或较远的时间点对电子2做测量，必定会测到 | 0 〉 〉 --> {\displaystyle |0\rangle } 的状态。因为投影式量子测量已经将原先量子态 ( | 00 〉 〉 --> 12 + | 11 〉 〉 --> 12 ) / 2 {\displaystyle (|00\rangle _{12}+|11\rangle _{12})/{\sqrt {2}}} 选择性地坍缩到 | 00 〉 〉 --> 12 {\displaystyle |00\rangle _{12}} ，也可写成 | 0 〉 〉 --> 1 | 0 〉 〉 --> 2 {\displaystyle |0\rangle _{1}|0\rangle _{2}} 或 | 0 〉 〉 --> 1 ⊗ ⊗ --> | 0 〉 〉 --> 2 {\displaystyle |0\rangle _{1}\otimes |0\rangle _{2}} 。这样，可以从电子1状态是 | 0 〉 〉 --> {\displaystyle |0\rangle } 知道选择到 | 00 〉 〉 --> {\displaystyle |00\rangle } 这一边。

注意到： | 0 〉 〉 --> 1 ⊗ ⊗ --> | 0 〉 〉 --> 2 {\displaystyle |0\rangle _{1}\otimes |0\rangle _{2}} 已经是两个成员系统各自量子态的张量积，所以测量后状态已非纠缠态。

参阅

量子隐形传态

爱因斯坦-波多尔斯基-罗森佯谬

相关不蕴涵因果

观测者效应

光子纠缠

量子相变

注释

^ 经典关联通常出自于某种守恒定律，例如，当零自旋π介子衰变成一个电子与一个正电子时，它们会遵守自旋守恒定律，从沿着同样轴向测量到的电子自旋可以预言正电子自旋 。

^ 假设爱丽丝先做测量电子的自旋，然后鲍勃再做测量，则当爱丽丝做测量之时刻，两个粒子彼此之间的量子关联也会变为经典关联 。

^ 复合系统是由多个粒子组成的系统。在粒子物理学里，除了基本粒子以外，其它所有的粒子都是复合系统；在多世界诠释里，整个宇宙是一个特大的波函数。所以，在区分复合系统与非复合系统方面，必须就各个案例而论。例如，在双缝实验里，照射粒子束于挡板的两条狭缝，移动通过狭缝的粒子内部结构并没有因此改变，并不是实验参数，只有整个粒子的位置、动量等等是实验参数，因此可以视粒子为非复合系统。但是，假设照射光子束于粒子，想要知道粒子是通过两条狭缝中的哪一条狭缝，这侦测动作会造成光子与粒子短暂时间耦合，因此必须将这粒子与光子视为一个复合系统。

^ 矩阵对数（logarithm of a matrix）也是矩阵；后者的矩阵指数等于前者。这是纯对数的推广。这运算是矩阵指数的反函数。并不是所有矩阵都有对数，有些矩阵有很多个对数。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。