定义

在数学上，一个在实数或复数a{\displaystyle a}邻域上的无穷可微实变函数或复变函数f(x){\displaystyle f(x)}的泰勒级数是如下的幂级数：

这里，n!{\displaystyle n!}表示n{\displaystyle n}的阶乘，而f(n)(a){\displaystyle f^{(n)}(a)\,\!}表示函数f{\displaystyle f}在点a{\displaystyle a}处的n{\displaystyle n}阶导数。如果a=0{\displaystyle a=0}，那么这个级数也可以被称为麦克劳伦级数。

解析函数

柯西在1823年指出函数exp⁡ ⁡ -->(− − -->1x2){\displaystyle \exp \left(-{\frac {1}{x^{2}}}\right)}在x=0{\displaystyle x=0}处不解析。

如果泰勒级数对于区间(a− − -->r,a+r){\displaystyle (a-r,a+r)}中的所有x{\displaystyle x}都收敛并且级数的和等于f(x){\displaystyle f(x)}，那么我们就称函数f(x){\displaystyle f(x)}为解析的（analytic）。当且仅当一个函数可以表示成为幂级数的形式时，它才是解析的。为了检查级数是否收敛于f(x){\displaystyle f(x)}，通常采用泰勒定理估计级数的余项。上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。

泰勒级数的重要性体现在以下三个方面：

幂级数的求导和积分可以逐项进行，因此求和函数相对比较容易。

一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数，并使得复分析这种手法可行。

泰勒级数可以用来近似计算函数的值。

对于一些无穷可微函数f(x){\displaystyle f(x)}虽然它们的展开式收敛，但是并不等于f(x){\displaystyle f(x)}。例如，分段函数f(x)=exp⁡ ⁡ -->(− − -->1x2){\displaystyle f(x)=\exp \left(-{\frac {1}{x^{2}}}\right)}，当x≠ ≠ -->0{\displaystyle x\neq 0}且f(0)=0{\displaystyle f(0)=0}，则当x=0{\displaystyle x=0}所有的导数都为零，所以这个f(x){\displaystyle f(x)}的泰勒级数为零，且其收敛半径为无穷大，虽然这个函数f{\displaystyle f}仅在x=0{\displaystyle x=0}处为零。而这个问题在复变函数内并不成立，因为当z{\displaystyle z}沿虚轴趋于零时exp⁡ ⁡ -->(− − -->1z2){\displaystyle \exp \left(-{\frac {1}{z^{2}}}\right)}并不趋于零。

一些函数无法被展开为泰勒级数因为那里存在一些奇点。但是如果变量x{\displaystyle x}是负指数幂的话，我们仍然可以将其展开为一个级数。例如，f(x)=exp⁡ ⁡ -->(− − -->1x2){\displaystyle f(x)=\exp \left(-{\frac {1}{x^{2}}}\right)}就可以被展开为一个洛朗级数。

Parker-Sochacki method（英语：Parker-Sochacki method）是最近发现的一种用泰勒级数来求解微分方程的定理。这个定理是对皮卡迭代的一个推广。

泰勒级数列表

在复平面上余弦函数的实数部分。

在复平面上余弦函数的第八度逼近

两个以上的曲线放在一起

下面我们给出了几个重要的泰勒级数。核函数x{\displaystyle x}为复数时它们依然成立。

几何级数：

二项式定理：

指数函数和自然对数：

三角函数：

双曲函数：

朗伯W函数：

多元函数的展开

泰勒级数可以推广到有多个变量的函数： ∑ ∑ -->n1=0∞ ∞ -->⋯ ⋯ -->∑ ∑ -->nd=0∞ ∞ -->∂ ∂ -->n1+⋯ ⋯ -->+nd∂ ∂ -->x1n1⋯ ⋯ -->∂ ∂ -->xdndf(a1,⋯ ⋯ -->,ad)n1!⋯ ⋯ -->nd!(x1− − -->a1)n1⋯ ⋯ -->(xd− − -->ad)nd{\displaystyle \sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {\partial ^{n_{1}+\cdots +n_{d}}}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}{\frac {f(a_{1},\cdots ,a_{d})}{n_{1}!\cdots n_{d}!}}(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}

历史

希腊哲学家芝诺在考虑了利用无穷级数求和来得到有限结果的问题，得出不可能的结论 -芝诺悖论。后来，亚里士多德对芝诺悖论在哲学上进行了反驳，但德谟克利特以及后来的阿基米德进行研究，此部分数学内容才得到解决。 正是用了阿基米德的穷举法才使得一个无穷级数被逐步的细分，得到了有限的结果。.几个世纪之后，中国数学家刘徽也独立提出了类似的方法。

进入14世纪，马德哈瓦（英语：Madhava of Sangamagrama）最早使用了泰勒级数以及相关的方法。尽管他的数学著作没有流传下来，但后来印度数学家的著作表明他发现了一些特殊的泰勒级数，这些级数包括正弦、余弦、正切、和反正切三角函数等等。之后，喀拉拉学派（英语：Kerala school of astronomy and mathematics）在他的基础上进行了一系列的延伸与合理逼近，这些工作一直持续到16世纪。

到了17世纪，詹姆斯·格雷果里同样继续着这方面的研究并且发表了若干麦克劳林级数。但是直到1715年，布鲁克·泰勒 提出了一个通用的方法来构建适用于所有函数的此类列级数。这就是后来被人们所熟知的泰勒级数。麦克劳林级数是泰勒级数的特例，是爱丁堡大学的科林·麦克劳林教授在18世纪发表的，并以其名字命名。

与牛顿插值公式的渊源

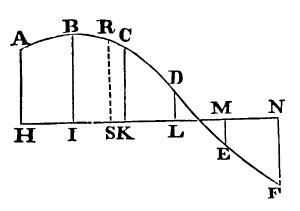
《自然哲学的数学原理》的第三编“宇宙体系”的引理五的图例。这里在横坐标上有6个点H,I,K,L,M,N，对应着6个值A,B,C,D,E,F，生成一个多项式函数对这6个点上有对应的6个值，计算任意点S对应的值R。牛顿给出了间距为单位值和任意值的两种情况。

牛顿插值公式也叫做牛顿级数，由“牛顿前向差分方程”的项组成，得名于伊萨克·牛顿爵士，最早发表为他在1687年出版的《自然哲学的数学原理》中第三编“宇宙体系”的引理五，此前詹姆斯·格雷果里于1670年和牛顿于1676年已经分别独立得出这个成果。一般称其为连续“泰勒展开”的离散对应。

差分

对于x值间隔为非一致步长，牛顿计算均差，对x值间隔为单位步长1或一致但非单位量的情况，计算差分，前向差分的定义为：

插值公式

牛顿插值公式为：

这成立于任何多项式函数和大多数但非全部解析函数。这里的表达式

是二项式系数，其中的(x)k是“下降阶乘幂”，空乘积(x)0被定义为1。

无穷级数

牛顿在1665年得出并在1671年写的《流数法》中发表了ln⁡ ⁡ -->(1+x){\displaystyle \ln(1+x)}的无穷级数，在1666年得出了arcsin⁡ ⁡ -->(x){\displaystyle \arcsin(x)}和arctan⁡ ⁡ -->(x){\displaystyle \arctan(x)}的无穷级数，在1669年的《分析学》中发表了sin⁡ ⁡ -->(x){\displaystyle \sin(x)}、cos⁡ ⁡ -->(x){\displaystyle \cos(x)}、arcsin⁡ ⁡ -->(x){\displaystyle \arcsin(x)}和ex{\display莱布尼茨e e^{x}}的无穷级数；莱布尼茨在1673年大概也得出了sin⁡ ⁡ -->(x){\displaystyle \sin(x)}、cos⁡ ⁡ -->(x){\displaystyle \cos(x)}和arctan⁡ ⁡ -->(x){\displaystyle \arctan(x)}的无穷级数。布鲁克·泰勒在1715年著作《Methodus Incrementorum Directa et Inversa》中研讨了有限差分方法，其中论述了他在1712年得出的泰勒定理，这个成果此前詹姆斯·约翰·伯努利670年和莱布尼茨在1673年已经得出，而约翰·伯努利在1694年已经在《教师学报》发表。

他对牛顿的均差分的步长取趋于0{\displaystyle 0}的极限，得出：

参见

无穷级数

牛顿多项式

幂级数

光滑函数

帕德近似

泰勒公式

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。