历史

 黎曼ζ函数在临界线Re(s) = 1/2上的实部（红色）和虚部（蓝色）。我们可以看到最起初的几个非平凡零点就位于Im(s) = ±14.135, ±21.022和±25.011上。

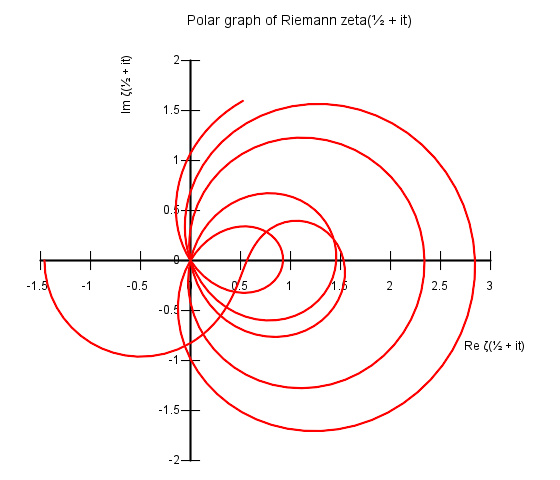
 黎曼ζ函数实部与虚部的数值比较图，也就是Re(ζ(s)) vs. Im(ζ(s))，沿着临界线s = it + 1/2，t 由0到34

黎曼1859年在他的论文《Über die Anzahl der Primzahlen unter einer gegebenen Größe》中提及了这个著名的猜想，但它并非该论文的中心目的，他也没有试图给出证明。黎曼知道ζ函数的不平凡零点对称地分布在直线s = ½ + it上，以及他知道它所有的不平凡零点一定位于区域0 ≤ Re(s) ≤ 1中。

1896年，雅克·阿达马和Charles Jean de la Vallée-Poussin分别独立地证明了在直线Re(s) = 1上没有零点。连同了黎曼对于不非凡零点已经证明了的其他特性，这显示了所有不平凡零点一定处于区域0 < Re(s) < 1上。这是素数定理第一个完整证明中很关键的一步。

1900年，大卫·希尔伯特将黎曼猜想包括在他著名的23条问题中，与哥德巴赫猜想一起组成了希尔伯特名单上的第8号问题。同时黎曼猜想也是希尔伯特问题中唯一一个被收入克雷数学研究所的千禧年大奖数学难题的。希尔伯特曾说，如果他在沉睡1000年后醒来，他将问的第一个问题便是：黎曼猜想得到证明了吗？

1914年，高德菲·哈罗德·哈代证明了有无限个零点在直线Re(s) = ½上。然而仍然有可能有无限个不平凡零点位于其它地方（而且有可能是最主要的零点）。后来哈代与约翰·恩瑟·李特尔伍德在1921年及塞尔伯格在1942年的工作（临界线定理）也就是计算零点在临界线Re(s) = ½上的平均密度。

近年来的工作主要集中于清楚的计算大量零点的位置（希望借此能找到一个反例）以及对处于临界线以外零点数目的比例置一上界（希望能把上界降至零）。

黎曼猜想与素数定理

黎曼猜想传统的表达式隠藏了这个猜想的真正重要性。黎曼ζ函数与素数的分布有着深厚的连结。Helge von Koch在1901年证明了黎曼猜想等价于素数定理一个可观的强化：给出任何ε > 0，我们有

式中π(x)为素数计数函数，ln(x)为x 的自然对数，以及右手边用上了大O符号。一个由Lowell Schoenfeld提出的非近似版本，表示黎曼猜想等价于

黎曼ζ函数的零点与素数满足一个称为明确公式的对偶性，这表明了：在调和分析的意义下，黎曼ζ函数的零点可视为素数分布的谐波。

将黎曼ζ函数代为更一般的L-函数，此时仍有相应的猜想：整体L-函数的非平凡零点的实部必等于 1 / 2 {\displaystyle 1/2} 。这被称为广义黎曼猜想。函数域上的广义黎曼猜想已被证明，数域的情形仍悬而未决。

黎曼猜想之结果及其等价命题

黎曼猜想的实际用途包括一些在黎曼猜想成立前提底下能被证明为真的命题，当中有些更被证明了跟黎曼猜想等价。其中一个就是以上素数定理误差项的增长率。

默比乌斯函数的增长率

其中一个命题牵涉了默比乌斯函数μ。命题“等式

在s的实部大于½的时候成立，而且右边项的和收敛”就等价于黎曼猜想。由此我们能够总结出假如Mertens函数的定义为

那黎曼猜想就等价于对任何 ε ε --> > 0 {\displaystyle \varepsilon >0} 都有

这将会对于M的增长给出了一个更紧的限制，因为即使没有黎曼猜想我们也能得出

（关于这些符号的意思，见大O符号。）

积性函数增长率

黎曼猜想等价于一些除μ(n)以外一些积性函数增长率的猜想。例如，约数函数σ(n)由下式给出：

那在n > 5040的时候，

这名为Robin定理并在1984年以Guy Robin命名。另一个有关的上限在2002年由Jeffrey Lagarias提出，他证明了黎曼猜想等价于命题“对于任意自然数n，

而 H n {\displaystyle H_{n}} 为第n个调和数 H n := 1 + 1 2 + … … --> + 1 n {\displaystyle H_{n}:=1+{\frac {1}{2}}+\ldots +{\frac {1}{n}}} 。

里斯判准与二项式系数和

里斯判准由里斯在1916年给出，它断言黎曼猜想等价于下式对所有 ϵ ϵ --> > 0 {\displaystyle \epsilon >0} 成立

哈代稍后于1918年以波莱尔求和法及梅林变换证明了下式的积分表法。

其它相关的积性函数的增长率也具有与黎曼猜想等价的表述。

考虑二项式系数和

Báez-Duarte与Flajolet、Brigitte Vallée证明了黎曼猜想等价于对所有的 ϵ ϵ --> > 0 {\displaystyle \epsilon >0} 下式成立

类似的还有以下级数

对此。Flajolet与Vepstas 证明了黎曼猜想等价于对所有的 ϵ ϵ --> > 0 {\displaystyle \epsilon >0} 下式成立

其中的 C ϵ ϵ --> {\displaystyle C_{\epsilon }} 是依赖于 ϵ ϵ --> {\displaystyle \epsilon } 的某个常数。

韦伊判准、李判准

韦伊判准断言某些函数的正定性等价于广义黎曼猜想。与此相似的还有李判准，这断言某些数列的正性等价于黎曼猜想。

跟法里数列的关系

另外两个跟黎曼猜想等价的命题牵涉了法里数列。假如Fn是法里数列中的第n项，由1/n开始而终于1/1，那命题“给出任何e > ½

”等价于黎曼猜想。在这里 m = ∑ ∑ --> i = 1 n ϕ ϕ --> ( i ) {\displaystyle m=\sum _{i=1}^{n}\phi (i)} 是法里数列中n阶项的数目。类似地等价于黎曼猜想的命题是“给出任何e > −1.

跟群论的关系

黎曼猜想等价于群论中的一些猜想。举例说，g（n），是对称群Sn的所有元素的秩之中，最大的一个，也就是兰道函数，则黎曼猜想等价于：对够大的n，下式成立：

临界线定理

黎曼猜想等价于命题“ ζ ζ --> ( s ) {\displaystyle \zeta (s)} 的导函数 ζ ζ --> ′ ( s ) {\displaystyle \zeta "(s)} 在区域

上无零点。” 函数ζ在临界线上只有单零点的充要条件是其导函数在临界线上非零。所以若黎曼猜想成立，命题中的非零区域可以延伸为 0 ( s ) ≤ ≤ --> 1 2 {\displaystyle 0 。这条进路带来了一些成果。Norman Levinson将此条件加细，从而得到了较强的临界线定理。

已否证的猜想

一些比黎曼猜想强的猜想曾被提出，但它们有被否证的趋势。Paul Turan证明了假如级数

当 R e ( s ) {\displaystyle Re(s)} 大于1时没有零点，则黎曼猜想成立，但Hugh Montgomery证明了这前提并不成立。另一个更强的默滕斯猜想也同样被否证。

相对弱的猜想

Lindelöf猜想

黎曼猜想有各种比较弱的结果；其中一个是关于ζ函数于临界线上的增长速度的Lindelöf猜想，表明了给出任意的e > 0，当t趋向无限，

记第n 个素数为pn，一个由Albert Ingham得出的结果显示，Lindelöf猜想将推导出“给出任意e > 0，对足够大的n 有

不过这个结果比大素数间隙猜想弱，详如下述。

大素数间隙猜想

另一个猜想是大素数间隙猜想。哈拉尔德·克拉梅尔证明了：假设黎曼猜想成立，素数p 与其后继者之间的间隙将会为 O ( p ln ⁡ ⁡ --> p ) {\displaystyle O({\sqrt {p}}\ln p)} 。平均来说，该间隙的阶仅为 O ( ln ⁡ ⁡ --> p ) {\displaystyle O(\ln p)} ，而根据数值计算结果，它的增长率并不似黎曼猜想所预测的那么大。

证明黎曼猜想的尝试

过去的一百多年，许多数学家声称证明了黎曼猜想。截至2015年为止，尚有一些证明还未被验证；但它们都被数学社群所质疑，多数专家并不相信它们是正确的。艾希特大学的Matthew R. Watkins为这些或是严肃或是荒唐的证明编辑了一份列表。其他一些证明可在arXiv数据库中找到。

黎曼猜想证明的可能的着手方向

由于黎曼猜想是有关2维变量（临界线（critical line）上的虚数解和黎曼ζ函数中的自然数变量n）的问题，故不但要考虑在2维变量下的情况，似乎还可以从更高维数（例如3或4维甚至更高维）变量的情况下来考虑问题。

另外，由于黎曼猜想从本质上来说是证明一个方程的非平凡的复数解必然是1/2+bi的形式（b是实数，i是虚数单位），因此应该与代数学是密不可分的；就是说，代数几何、代数数论甚至代数拓扑等学科的知识是不可缺少的。如果能从上述几个分支学科之间找到新的联系，以及对这些分支学科有进一步的新发现，那可能可以为证明黎曼猜想打下基础，或为黎曼猜想的证明做好准备。

与算子理论的可能联系

长久以来，人们猜测黎曼猜想的“正解”是找到一个适当的自伴算符，再由实特征值的判准导出 ζ ζ --> ( s ) {\displaystyle \zeta (s)} 零点实部的资讯。在此方向上已有许多工作，却仍未有决定性的进展。

黎曼ζ函数的统计学性质与随机矩阵的特征值有许多相似处。这为希尔伯特-波利亚猜想提供了一些支持。

在1999年，Michael Berry与Jon Keating猜想经典哈密顿函数 H = x p {\displaystyle H=xp} 有某个未知的量子化 H ^ ^ --> {\displaystyle {\hat {H}}} ，使得下式成立

更奇特的是，黎曼ζ函数的零点与算子 1 / 2 + i H ^ ^ --> {\displaystyle 1/2+i{\hat {H}}} 的谱相同。正则量子化的情形则相反：正则量子化引致海森堡测不准原理 [ x , p ] = 1 / 2 {\displaystyle [x,p]=1/2} ，并使量子谐振子的谱为自然数。重点在于，所求的哈密顿算符应当是个闭自伴算符，方能满足希尔伯特-波利亚猜想之要求。

搜寻ζ函数的零点

  ζ函数的绝对值。

关于计算上找寻ζ函数零点越多越好的尝试，已经有一段很长的历史了。其中一个出名的尝试乃ZetaGrid，一个分散式计算的计划，一天可检查上十亿个零点。这计划在2005年11月终止。直至2006年，没有计算计划成功找到黎曼猜想的一个反例。

2004年，Xavier Gourdon与Patrick Demichel透过Odlyzko-Schönhage algorithm验证了黎曼猜想的头十兆个非平凡零点。

Michael Rubinstein给了公众一个算法去算出零点。

参考文献

历史文献

Bernhard Riemann, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, (1859) Monatsberichte der Berliner Akademie.

Jacques Hadamard, Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques, Bulletin Société Mathématique de France 14 (1896) pp 199-220.

现代技术参考

H. M. Edwards, Riemann"s Zeta Function, Academic Press, 1974. (Reprinted by Dover Publications, 2001 ISBN 0-486-41740-9)

E. C. Titchmarsh, The Theory of the Riemann Zeta Function, second revised (Heath-Brown) edition, Oxford University Press, 1986

Jeffrey Lagarias, An Elementary Problem Equivalent to the Riemann Hypothesis, American Mathematical Monthly (2002), no. 109, 534--543（论及与和谐数的关联）

Computation of zeros of the Zeta function (2004).（关于GUE猜想的评论，兼具丰富的书目资料。）

Schoenfeld, Lowell. "Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II." Mathematics of Computation30 (1976), no. 134, 337--360.

Conrey, J. Brian. "the Riemann Hypothesis" Notices of the American Mathematical Society, March 2003, 341-353.可自由下载。

受欢迎的参考资料

Clay Mathematics Institute, Millennium Problems, (2000)

Marcus du Sautoy, The Music of the Primes, HarperCollins, 2003

Marcus du Sautoy, "Prime Numbers Get Hitched", Seed Magazine" (03/27/2006)

Daniel Rockmore, Stalking the Riemann Hypothesis : The Quest to Find the Hidden Law of Prime Numbers, Pantheon Books, New York, 2005. ISBN 0-375-42136-X.

John Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics, Joseph Henry Press (April 23, 2003), ISBN 0-309-08549-7. 448 page

Zetagrid (2002)试图否证黎曼猜想的分散式计算计划，已于2005年11月终止。

Ed Pegg, Jr., Ten Trillion Zeta Zeros, (2004)讨论Xavier Gourdon对前十兆个非平凡零点的计算。

de Vries, The Graph of the Riemann Zeta function ζ(s) (2004).

Erica Klarreich, "Prime Time", New Scientist - November 11, 2000, p. 32.对黎曼猜想的简介。

QEDen A wiki dedicated to solving the millennium problems

引用来源

Bollobas, Bela, foreword to Littlewood"s Miscellany, Cambridge University Press, 1986

参见

埃拉托斯特尼筛法

素数

素数公式

素数判定法则

广义黎曼猜想

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。