历史

  格奥尔格·欧姆。

早于1753年，意大利物理学家乔凡尼·贝卡立亚（ Giovanni Beccaria ）就在研究物质的导电性质。他在电路里加装了盛满了水的玻璃管。当开启电路后，发现玻璃管的截面面积越大，电流的放电强度越大 。

亨利·卡文迪什也做了很多实验，研究电动势、电流、电阻之间的关系。他使用莱顿瓶为电流源，将电流通过在各种尺寸的玻璃试管里盛装的盐溶液，靠着调整盐溶液的高度，他可以控制放电强度。卡文迪什把自己身体当作一台生理检流计，从亲身体验被电击后的感觉，来估计电流的放电强度。他又选择出一个装满盐溶液的玻璃试管为标准，然后比较标准放电与试样放电，按照放电强度的大小来估计它们的电阻。这样，他可以定量地描述每一种试样。于1781年1月，他记录在笔记里，电流与电动势成正比。但是，他并没有将这些珍贵的实验结果告诉任何科学家。一直到麦克斯韦于1879年替他编辑注释为著作《卡文迪什的电学研究》（ The electrical researches of the Honourable Henry Cavendish ）后，才见诸世面 。注意到卡文迪什使用的仪器相当原始粗陋，靠身体感觉很难做出精准的测量，莱顿瓶并不是稳定电流源。所以，学术界认为这耽搁了近百年的实验结果并不足以证实欧姆定律。

从1825年到1826年之间，欧姆做了很多关于电阻的实验。于1827年，他将得到的结果一同发表在著作《直流电路的数学研究》（The galvanic Cirt investigated mathematically）里 。他从傅里叶对于热传导的研究得到了相当多的灵感，借用了很多傅里叶的点子来论述自己的结果。

欧姆是一位优秀的实验者，很会设计与制造实验设备，又具有精湛的数学修养与严谨的敬业态度。刚开始，他使用伏打电堆为电源，用安装于扭秤（torsion balance）的磁针来测量电流的磁场力。载流导线的电流所产生的磁场与电流成正比，只要测量在载流导线附近的磁针所感受到的磁场力，就可以知道电流。他将电流通过不同长度的检验电线；由于长度不同，电阻也不同。欧姆仔细分析实验结果，得到经验方程

其中， Δ Δ --> I {\displaystyle \Delta I} 是检验电线造成的电流差值， m {\displaystyle m} 是跟实验参数有关的系数， x {\displaystyle x} 是检验电线的长度， a {\displaystyle a} 是跟固定长度的载流导线有关的常数。

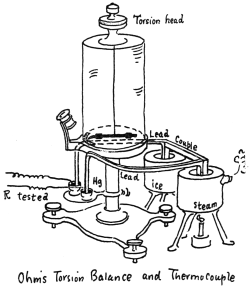
  欧姆的实验设备。由于温差，热电偶会产生电动势，促成电流流动于电阻电路。这电流又会产生磁场，使得固定于扭秤的磁针偏转。从读取磁针偏转的角度，就可以知道电流。

欧姆很快地就觉得这方程不太对劲。大约三年前，汤玛斯·泽贝克（ Thomas Seebeck ）发明使用热电偶为电源。这种电源比伏打电源稳定。采纳《物理与化学年鉴》的总编辑约翰·波根多夫（ Johann poggendorff ）的建议，欧姆改用热电偶为电源 ，将实验重做一遍，得到经验方程：

其中， X {\displaystyle X} 是扭秤读值， a {\displaystyle a} 是跟电动势有关的常数， b {\displaystyle b} 是跟内部电阻有关的常数， x {\displaystyle x} 是检验电线的长度。

仔细诠释这些变量，将 X {\displaystyle X} 、 a {\displaystyle a} 、 b {\displaystyle b} 、 x {\displaystyle x} 分别诠释为电流 I {\displaystyle I} 、电压 V {\displaystyle V} 、内部电阻 r {\displaystyle r} 、检验电阻 R x {\displaystyle R_{x}} ，那么，假定总电阻 R {\displaystyle R} 为 r + R x {\displaystyle r+R_{x}} 则经验方程变为欧姆定律的现代方程版本：

欧姆定律可能是早期电学史最重要的定量理论。但是，当欧姆最初发表他的结果时，很多学术界同仁都激烈地批评反对他的理论。德国教育部长指责：“鼓吹这种异端邪说的教授不配教导科学 。”物理教授格奥尔格·魄尔（ Georg Pohl ）这样批评欧姆的著作：“以崇高眼光仰看这世界的人士，必须远离这本无可救药、妄生穿凿的谬书，其唯一目的乃是彻底诋毁大自然的尊严 。”。那时候，德国正盛行的黑格尔哲学认为，因为大自然井井有序，而且只要经过合理推论就可获得科学真理，所以，并不需要靠做实验来了解大自然。欧姆的实验方法可能引起了黑格尔门徒的强烈反感。

1839年，法国物理学家，克劳德·普雷特（ Claude Pouillet ）确定欧姆的实验结果。同时，欧姆成为柏林科学院的院士。在英国，查尔斯·惠斯通（ Charles Wheatstone ）又重新核对了欧姆的实验结果。1841年，欧姆被选为皇家学会的外籍会员。1852年，欧姆荣膺为慕尼黑大学的物理学系主任。

于1920年，物理学家发现，通过理想电阻器的电流会出现统计涨落，虽然当电压和电阻为常数时，统计涨落会跟温度有关。这种涨落称为詹森-奈奎斯特噪音（ Johnson–Nyquist noise ），是因为电荷的离散秉性而产生的现像。这热效应意味着，假若取样的时间间隔足够短暂，电流或电压的测值，其比例跟时间平均比例或系综平均（ ensemble average ）比例相比较，会出现涨落；也就是说，每一个电阻 R {\displaystyle R} 的取样值，跟 R {\displaystyle R} 的时间平均或系综平均相比较，会出现涨落。对于普通电阻物质案例，经过平均程序后，欧姆定律仍旧正确无误。

欧姆对于电阻的研究在麦克斯韦方程组出现之前很久，那时科学家对于交流电路的频率相关效应也不了解。但是，在适当范围内，现代电磁理论与现代电路理论并没有发现任何与欧姆定律相悖之处。

水力学类比

欧姆定律可以用水力学类比（ hydraulic analogy ）来描述。测量单位为帕斯卡的水压，可以类比为电压。在一根水管里，由于任意两点之间的水压差会造成水流，水的流速（单位是升每秒），可以类比为电流（单位是库仑每秒）。“流量限制器”是安装于水管与水管之间控制流量的阀门，可以类比为电阻器。通过流量限制器的水流流量，跟流量限制器两端的水压成正比，类似地，通过电阻器的电荷流量（电流），跟电阻器两端的电压成正比。这正是欧姆定律的论述。

流体流动网络的流量和流压可以用水力学类比方法来计算 。这方法可以应用于稳定流和暂态流（ transient flow ）。对于线性层流，泊肃叶定律（ Poiseuille"s law ）描述水管的水阻，但是对于湍流，流压-流量关系变为非线性。

热力学类比

设定导电体的电导率与两端的电压，欧姆定律可以预测出通过这导电体的电流密度。类似地，设定导热体的热导率与两端的温差，约瑟夫·傅里叶的热传导定律可以预测通过这导热体的热流 。同样的方程形式可以描述这两种现象。对于每一种案例，方程的变量有不同的意义。具体而言，欧姆定律的方程为：

而热传导定律的方程为：

其中， Γ Γ --> {\displaystyle {\boldsymbol {\Gamma }}} 是热通量（ heat flux ）， k {\displaystyle k} 是导热体的热导率， T {\displaystyle T} 是温度。

思考参数为温度、热导率与热通量的热传导问体，和参数为电压、电导率与电流密度的电传导问体。这两个问题相互等价。假若能够解析一个热传导问体，则也能够解析电传导问题；反之亦然。

电路分析

在电路学里，电阻器（欧姆电阻器）是一种电路元件，其电阻与电压、电流无关。电阻器可以按照欧姆定律阻抗电荷的通过。每一个电阻器都有其设计制成的电阻 R {\displaystyle R} 。更严格地说，电阻器是在某操作域内遵守欧姆定律的电路元件；欧姆定律和唯一电阻值足够描述这元件在相关操作域的行为。

串联电阻电路

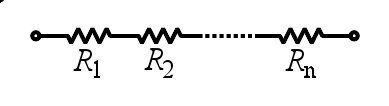
 n {\displaystyle n} 个电阻器串联形成的电路。

串联电阻的总电阻等于各个电阻之和，以方程表示，

其中， R n {\displaystyle R_{n}} 是第 n {\displaystyle n} 个电阻， R t o t a l {\displaystyle R_{\mathrm {total} }} 是总电阻。

假设在电路两端的电压为 V {\displaystyle V} ，则通过的电流为 I = V / R t o t a l {\displaystyle I={V}/{R_{total}}} 。假设每一个电阻器都遵守欧姆定律，则这电路是电阻为 R t o t a l {\displaystyle R_{\mathrm {total} }} 的欧姆电路。

并联电阻电路

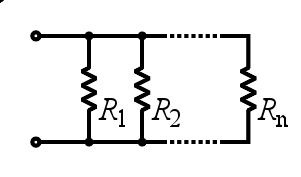
 n {\displaystyle n} 个电阻器并联形成的电路。

相互并联的电阻，其总电阻的倒数等于其每个电阻的倒数和，以方程表示：

假设在电路两端的电压为 V {\displaystyle V} ，则通过的电流为 I = V / R t o t a l {\displaystyle I={V}/{R_{total}}} 。假设每一个电阻器都遵守欧姆定律，则这电路是电阻为 R t o t a l {\displaystyle R_{\mathrm {total} }} 的欧姆电路。

周期性激发

电容器、电感器、传输线等等，都是电路的电抗元件。假设施加周期性电压或周期性电流于含有电抗元件的电路，则电压与电流之间的关系式变成微分方程。因为欧姆定律的方程只涉及实值的电阻，不涉及可能含有电容或电感的复值阻抗，所以，前面阐述的欧姆定律不能直接应用于这状况。

最基本的周期性激发，像正弦激发或余弦激发，都可以用指数函数来表达：

其中， j {\displaystyle j} 是虚数单位， ω ω --> {\displaystyle \omega } 是实值角频率， t {\displaystyle t}时间是时间。

假设周期性激发为单频率正弦激发，其角频率为 ω ω --> {\displaystyle \omega } 。电阻为 R {\displaystyle R} 的电阻器，其阻抗 Z {\displaystyle {Z}} 为：

电感为 L {\displaystyle L} 的电感器，其阻抗为：

电容为 C {\displaystyle C} 的电容器，其阻抗为：

电压 V {\displaystyle {V}} 与电流 I {\displaystyle {I}} 的关系式为：

注意到将阻抗 Z {\displaystyle {Z}} 替代电阻 R {\displaystyle R} ，就可以得到这欧姆定律方程的推广。只有 Z {\displaystyle {Z}} 的实值部分会造成热能的耗散。

对于这系统，电流和电压的复值波形式分别为：

电流和电压的实值部分 r e a l ( I ) {\displaystyle real({I})} 、 r e a l ( V ) {\displaystyle real({V})} 分别描述这电路的真实正弦电流和正弦电压。由于 I 0 {\displaystyle {I}_{0}} 、 V 0 {\displaystyle {V}_{0}} 都是不同的复值标量，电流和电压的相位可能会不一样。

周期性激发可以傅里叶分解为不同角频率的正弦函数激发。对于每一个角频率的正弦函数激发，可以使用上述方法来计算响应。然后，将所有响应总和起来，就可以得到解答。

线性近似

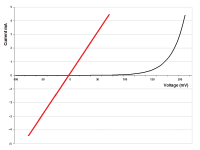
  电流对电压线图。理想电阻器和PN接面二极管的V-I线分别以红色和黑色显示。

欧姆定律是电路分析（ cirt analysis ）使用的几个基本方程之一。它可以应用于金属导电体或特别为这行为所制备的电阻器。在电机工程学里，这些东西无所不在。遵守欧姆定律的物质或元件称为“欧姆物质”或“欧姆元件”。理论上，不论施加的电压或电流、不论是直流或交流、不论是正极或负极，它们的电阻都不变 。

但是，有些电路元件不遵守欧姆定律，它们的电压与电流之间的关系（V-I线）乃非线性关系。PN接面二极管是一个显明范例。如右图所示，随着二极管两端电压的递增，电流并没有线性递增。给定外电压，可以用V-I线来估计电流，而不能用欧姆定律来计算电流，因为电阻会因为电压的不同而改变。另外，只有当外电压为正值时，电流才会显著地递增；当施加的电压为负值时，电流等于零。对于这类元件，V-I线的斜率 r {\displaystyle {\mathfrak {r}}} ，称为“小信号电阻”（ small-signal resistance ）、“增量电阻”（ incremental resistance ）或“动态电阻”（ dynamic resistance ），定义为

单位也是欧姆，是很重要的电阻量，适用于计算非欧姆元件的电性 。

温度效应

詹姆斯·麦克斯韦诠释欧姆定律为，处于某状态的导电体，其电动势与产生的电流成正比。因此，电动势与电流的比例，即电阻，不会随着电流而改变。在这里，电动势就是导电体两端的电压。参考这句引述的上下文，修饰语“处于某状态”，诠释为处于常温状态，这是因为物质的电阻率通常跟温度有关。根据焦耳定律，导电体的焦耳加热（ Joule heating ）与电流有关，当传导电流于导电体时，导电体的温度会改变。电阻对于温度的相关性，使得在典型实验里，电阻跟电流有关，从而很不容易直接核对这形式的欧姆定律。于1876年，麦克斯韦与同事，共同设计出几种测试欧姆定律的实验方法，能够特别凸显出导电体对于加热效应的响应 。

其它版本的欧姆定律

在电机工程学和电子工程学里，欧姆定律妙用无穷，因为它能够在宏观层次表达电压与电流之间的关系，即电路元件两端的电压与通过的电流之间的关系。在物理学里，对于物质的微观层次电性质研究，会使用到的欧姆定律，以矢量方程表达为：

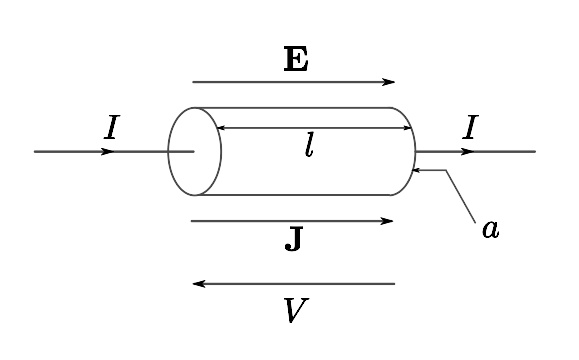
  处于均匀外电场的均匀截面导电体（例如，电线）。

在导体内任意两点g、h，定义电压为将单位电荷从点g移动到点h，电场力所需做的机械功：

其中， V g h {\displaystyle V_{gh}} 是电压， w {\displaystyle w} 是机械功， q {\displaystyle q} 是电荷量， d l {\displaystyle \mathrm {d} \mathbf {l} } 是微小线元素。

假设，沿着积分路径，电流密度 J = J l ^ ^ --> {\displaystyle \mathbf {J} =J{\hat {\mathbf {l} }}} 为均匀电流密度，并且平行于微小线元素：

其中， l ^ ^ --> {\displaystyle {\hat {\mathbf {l} }}} 是积分路径的单位矢量。

那么，可以得到电压：

其中， l {\displaystyle l} 是积分路径的径长。

假设导体具有均匀的电阻率，则通过导体的电流密度也是均匀的：

其中， a {\displaystyle a} 是导体的截面面积。

电压 V g h {\displaystyle V_{gh}} 简写为 V {\displaystyle V} 。电压与电流成正比：

总结，电阻与电阻率的关系为：

假设 J > 0 {\displaystyle J>0} ，则 V > 0 {\displaystyle V>0} ；将单位电荷从点g移动到点h，电场力需要作的机械功 w > 0 {\displaystyle w>0} 。所以，点g的电势比点h的电势高，从点g到点h的电势差为 − − --> V {\displaystyle -V} 。从点g到点h，电压降是 V {\displaystyle V} ；从点h到点g，电压升是 V {\displaystyle V} 。

给予一个具有完美晶格的晶体，移动于这晶体的电子，其运动等价于移动于自由空间的具有有效质量（ effective mass ）的电子的运动。所以，假设热运动足够微小，周期性结构没有偏差，则这晶体的电阻等于零。但是，真实晶体并不完美，时常会出现晶体缺陷（ crystallographic defect ），有些晶格点的原子可能不存在，可能会被杂质侵占。这样，晶格的周期性会被扰动，因而电子会发生散射。另外，假设温度大于绝对温度，则处于晶格点的原子会发生热震动，会有热震动的粒子，即声子，移动于晶体。温度越高，声子越多。声子会与电子发生碰撞，这过程称为晶格散射（ lattice scattering ）。主要由于上述两种散射，自由电子的流动会被阻碍，晶体因此具有有限电阻 。

凝聚态物理学研究物质的性质，特别是其电子结构。在凝聚态物理学里，欧姆定律更复杂、更广义的方程非常重要，属于本构方程（ constitutive equation ）与运输系数理论（ theory of transport coefficients ）的范围。

经典微观表述

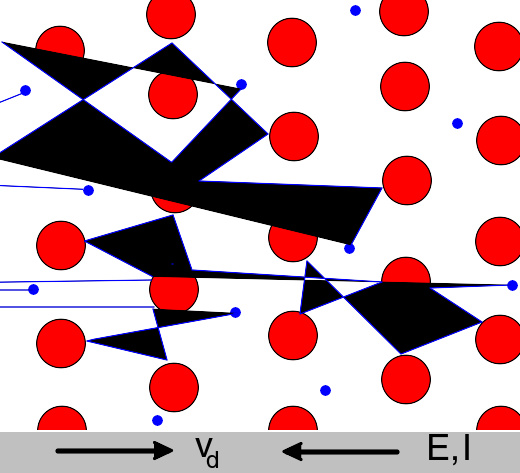
  在德鲁德模型里，电子（以蓝色表示）不停地在固定不动的导电体离子（以红色表示）之间移动与碰撞。假若施加电场于导电体，则电子的平均移动速度（称为漂移速度）不等于零。电子的漂移速度方向与电场方向相反。

当施加外电场于导电体时，电流密度的响应，基本上是属于量子力学性质。详尽细节，请参阅经典与量子电导率（ classical and quantum conductivity ）。保罗·德鲁德于1900年研究出的德鲁德模型，可以用经典物理解释欧姆定律，描述自由电子移动于金属导电体的物理行为 。

在德鲁德模型里，自由电子会不停地移动碰撞于固定不动、组成整个金属导电体晶格的正价离子之间。金属里的每一个自由电子，感受到电场力的作用，会呈加速运动。但是每当自由电子与晶格发生碰撞，其动能会遭受损失，以热能的形式将能量释放给离子，所以，电子的平均移动速度是漂移速度，其漂移速度的方向与电场方向相反。

电子感受到的平均电场力 F a v e {\displaystyle \mathbf {F} _{ave}} 为：

其中， E a v e {\displaystyle \mathbf {E} _{ave}} 是平均电场， e {\displaystyle e} 是单位电荷量。

德鲁德计算出漂移速度 v d {\displaystyle \mathbf {v} _{d}} 为：

其中， τ τ --> {\displaystyle \tau } 是平均自由时间（ mean free time ），是碰撞之间的平均时间间隔， m {\displaystyle m} 是电子的质量。

在金属里，电荷载子为电子，所以电流密度与漂移速度的关系为：

其中， n {\displaystyle n} 是电子密度。

假设电场是均匀电场， E = E a v e {\displaystyle \mathbf {E} =\mathbf {E} _{ave}} ，设定电阻率为：

则电场与电流密度的关系为：

注意到漂移速率 v d {\displaystyle v_{d}} 超小于热速率 v t {\displaystyle v_{t}} ，

其中， k B {\displaystyle k_{B}} 是玻尔兹曼常量， T {\displaystyle T} 是温度。

因此，平均自由时间与热速率有关，与漂移速率无关，所以平均自由时间也与电流密度、电场无关。质量、电子密度、单位电荷，都与电流密度、电场无关。总结，电阻率与电流密度、电场无关。

磁效应

前面得到的答案只成立于导电体的参考系。在经典电磁学里，假设处于磁场 B {\displaystyle \mathbf {B} } 的导电体，以相对速度 v 0 {\displaystyle \mathbf {v} _{0}} 移动于磁场的参考系 S {\displaystyle {\mathcal {S}}} ，则电子感受到的平均洛伦兹力 F a v e {\displaystyle \mathbf {F} _{ave}} 为：

漂移速度 v d {\displaystyle \mathbf {v} _{d}} 为：

电场与电流密度的关系为：

所以，欧姆定律的形式推广为：

参阅

薄膜电阻

菲克扩散定律

霍普金森定律（ Hopkinson"s law ，静磁学的欧姆定律）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。