定理

在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：

余弦定理是勾股定理的一个推广 。勾股定理现约有400种证明方法，是数学定理中证明方法最多的定理之一 。

其他形式

如果c是斜边的长度而a和b是另外两条边的长度，勾股定理可以写成：

a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}\,}

如果a和b知道，c可以这样写：

c = a 2 + b 2 . {\displaystyle c={\sqrt {a^{2}+b^{2}}}.\,}

如果斜边的长度c和其中一条边（a或b）知道，那另一边的长度可以这样计算：

或

勾股数组

勾股数组 是满足勾股定理 a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} 的正整数组 ( a , b , c ) {\displaystyle (a,b,c)} ，其中的 a , b , c {\displaystyle a,b,c} 称为 勾股数 。例如 ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} 就是一组勾股数组。

任意一组勾股数 ( a , b , c ) {\displaystyle (a,b,c)} 可以表示为如下形式： a = k ( m 2 − − --> n 2 ) , b = 2 k m n , c = k ( m 2 + n 2 ) {\displaystyle a=k(m^{2}-n^{2}),b=2kmn,c=k(m^{2}+n^{2})} ，其中 k , m , n ∈ ∈ --> N ∗ ∗ --> , m > n {\displaystyle k,m,n\in \mathbb {N*} ,m>n} 。

历史

公元前18世纪记录各种勾股数组的巴比伦石板

这个定理的历史可以被分成三个部分：发现勾股数、发现直角三角形中边长的关系、及其定理的证明。

勾股数

勾股数出现得较早，例如埃及的纸草书里面就有（3,4,5）这一组勾股数，而巴比伦泥板涉及的最大的一个勾股数组是（18541，12709，13500）。后来的中国的算经、印度与阿拉伯的数学书也有记载 。在中国，《周髀算经》中也记述了(3,4,5)这一组勾股数，商高答周公问曰：“勾广三，股备四，径隅五”；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释：“勾股个自乘，并之，为弦实，开方除之，即弦”。《九章算术》卷第九《句股》章详细讨论了勾股定理的运用，魏国数学家刘徽反复运用勾股定理求圆周率。

金朝数学家李冶的《测圆海镜》通过勾股容圆图式的十五个勾股形和直径的关系，建立了系统的天元术，推导出692条关于勾股形的各边的公式，其中用到了多组勾股数作为例子。

普遍定理的发现

巴比伦人得到的勾股数的数量和质量不太可能纯从测量手段获得。之后的毕达哥拉斯本人并无著作传世，不过在他死后一千年，5世纪的普罗克勒斯给欧几里德的名著《几何原本》做注解时将最早的发现和证明归功于毕达哥拉斯学派：

普鲁塔克和西塞罗也将发现的功劳归于毕达哥拉斯，但没有任何证据表明毕达哥拉斯证明了勾股定理，以素食闻名的毕达哥拉斯杀牛更是不可思议。

在中国，记载秦朝的算数书并未记载勾股定理，只是记录了一些勾股数。定理首次载于书面则是在成书于西汉但内容收集整理自公元前一千多年以来的《周髀算经》“荣方问于陈子”一节中：

因此有些人将这个定理称之为陈子定理。

东汉末年赵爽《周髀算经注》《勾股圆方图注》记载：

赵爽《勾股圆方图》

在《九章算术注》中，刘徽反复利用勾股定理求圆周率，并利用“割补术”做“青朱出入图”完成勾股定理的几何图形证明。

直至现时为止，仍有许多关于勾股定理是否不止一次被发现的辩论。

证明

毕达哥拉斯学派的证明没有流传下来，流传下来的勾股定理的书面证明最早见于几何原本第一册的第47个命题。在中国，东汉末年吴国的赵爽最早给出勾股定理的证明。最近， 巴勒蒂·克尔什纳·蒂尔特吉 （ 英语 ： Bharati Krishna Tirthaji ） 在吠陀数学一书中声称古代印度教吠陀证明了勾股定理。

证明

这个定理有许多证明的方法，其证明的方法可能是数学众多定理中最多的。路明思（Elisha Scott Loomis）的 Pythagorean Proposition 一书中总共提到367种证明方式。

有人会尝试以三角恒等式（例如：正弦和余弦函数的泰勒级数）来证明勾股定理，但是，因为所有的基本三角恒等式都是建基于勾股定理，所以不能作为勾股定理的证明（参见循环论证）。

赵爽勾股圆方图证明法

中国三国时期赵爽为证明勾股定理作“勾股圆方图”即“弦图”，按其证明思路，其法可涵盖所有直角三角形，为东方特色勾股定理无字证明法。2002年第24届国际数学家大会（ICM）在北京召开。中国邮政发行一枚邮资明信片，邮资图就是这次大会的会标—中国古代证明勾股定理的赵爽弦图。

赵爽 勾股圆方图证明勾股定理法动画

刘徽“割补术”证明法

中国魏晋时期伟大数学家刘徽作《九章算术注》时，依据其“割补术”为证勾股定理另辟而作“青朱出入图”。刘徽描述此图，“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂。开方除之，即弦也。 ”其大意为，一个任意直角三角形，以勾宽作红色正方形即朱方，以股长作青色正方形即青方。将朱方、青方两个正方形对齐底边排列，再进行割补—以盈补虚，分割线内不动，线外则“各从其类”，以合成弦的正方形即弦方，弦方开方即为弦长。

刘徽 青朱出入图

利用相似三角形的证法

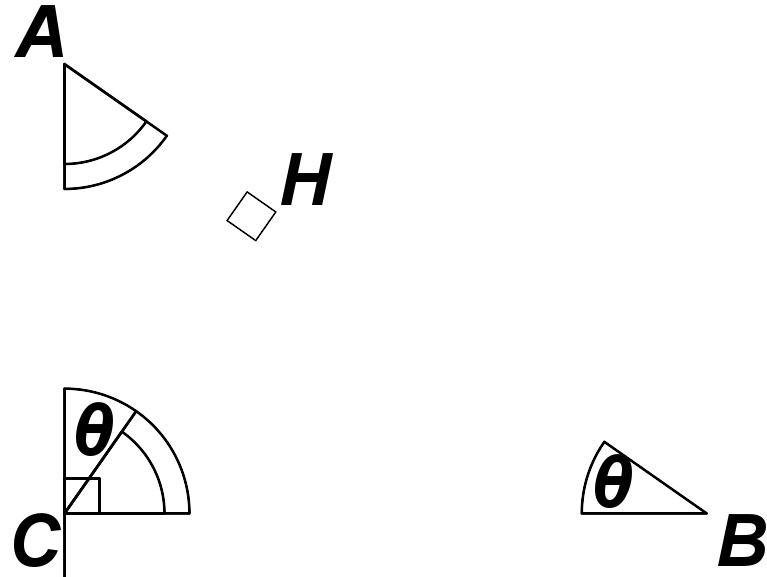
相似三角形的证明

有许多勾股定理的证明方式，都是基于相似三角形中两边长的比例。

设 ABC 为一直角三角形，直角于角 C （看右图）。从点 C 画上三角形的高，并将此高与 AB 的交叉点称之为 H 。此新三角形 ACH 和原本的三角形 ABC 相似，因为在两个三角形中都有一个直角（这又是由于“高”的定义），而两个三角形都有 A 这个共同角，由此可知第三只角都是相等的。同样道理，三角形CBH和三角形ABC也是相似的。这些相似关系衍生出以下的比率关系：

因为

所以

可以写成

综合这两个方程式，我们得到

换句话说:

欧几里得的证法

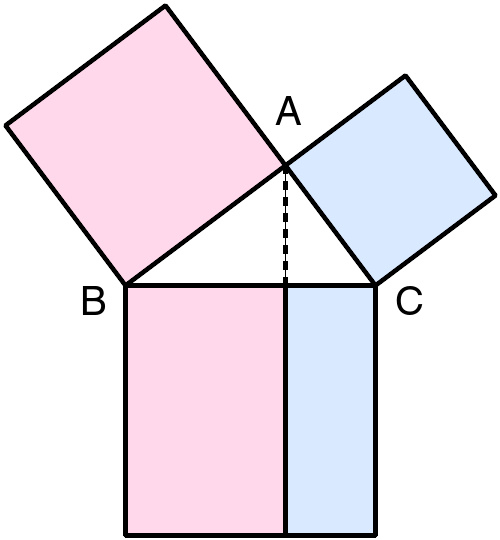
《几何原本》中的证明

在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ ABC 为一直角三角形，其中 A 为直角。从 A 点划一直线至对边，使其垂直于对边。延长此线把对边上的正方形一分为二，其面积分别与其余两个正方形相等。

在定理的证明中，我们需要如下四个辅助定理：

如果两个三角形有两组对应边和这两组边所夹的角相等，则两三角形全等。（SAS定理）

三角形面积是任一同底同高之平行四边形面积的一半。

任意一个正方形的面积等于其二边长的乘积。

任意一个矩形的面积等于其二边长的乘积（据辅助定理3）。

证明的思路为：把上方的两个正方形，透过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形。

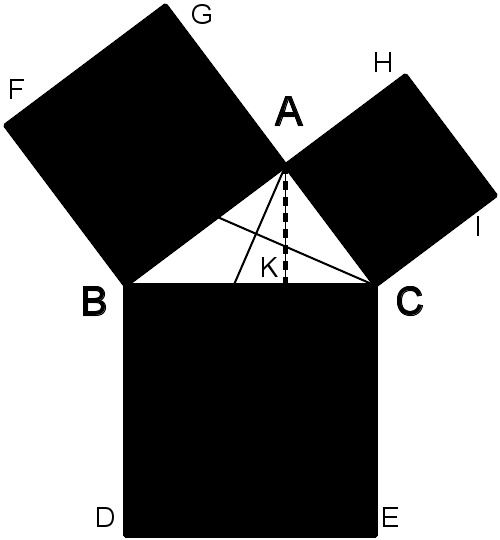
证明辅助图2

其证明如下：

设 △ △ --> A B C {\displaystyle \triangle ABC} 为一直角三角形，其直角为CAB。

其边为BC、AB、和CA，依序绘成四方形CBDE、BAGF和ACIH。

画出过点A之BD、CE的平行线。此线将分别与BC和DE直角相交于K、L。

分别连接CF、AD，形成两个三角形BCF、BDA。

∠ ∠ --> C A B {\displaystyle \angle CAB} 和 ∠ ∠ --> B A G {\displaystyle \angle BAG} 都是直角，因此C、A和G都是共线的，同理可证B、A和H共线。

∠ ∠ --> C B D {\displaystyle \angle CBD} 和 ∠ ∠ --> F B A {\displaystyle \angle FBA} 皆为直角，所以 ∠ ∠ --> A B D {\displaystyle \angle ABD} 全等于 ∠ ∠ --> F B C {\displaystyle \angle FBC} 。

因为AB和BD分别等于FB和BC，所以 △ △ --> A B D {\displaystyle \triangle ABD} 必须相等于 △ △ --> F B C {\displaystyle \triangle FBC} 。

因为A与K和L在同一直线上，所以四方形BDLK必须二倍面积于 △ △ --> A B D {\displaystyle \triangle ABD} 。

因为C、A和G在同一直线上，所以正方形BAGF必须二倍面积于 △ △ --> F B C {\displaystyle \triangle FBC} 。

因此四边形BDLK必须和BAGF有相同的面积= A B 2 {\displaystyle AB^{2}} 。

同理可证，四边形CKLE必须有相同的面积ACIH = A C 2 {\displaystyle AC^{2}} 。

把这两个结果相加， A B 2 + A C 2 = B D × × --> B K + K L × × --> K C {\displaystyle AB^{2}+AC^{2}=BD\times BK+KL\times KC}

由于 B D = K L {\displaystyle BD=KL} ， B D × × --> B K + K L × × --> K C = B D ( B K + K C ) = B D × × --> B C {\displaystyle BD\times BK+KL\times KC=BD\left(BK+KC\right)=BD\times BC}

由于CBDE是个正方形，因此 A B 2 + A C 2 = B C 2 {\displaystyle AB^{2}+AC^{2}=BC^{2}} 。

此证明是于欧几里得《几何原本》一书第1.47节所提出的

由于这个定理的证明依赖于平行公理，而且从这个定理可以推出平行公理，很多人质疑平行公理是这个定理的必要条件，一直到十九世纪尝试否定第五公理的非欧几何出现。

图形重新排列证法

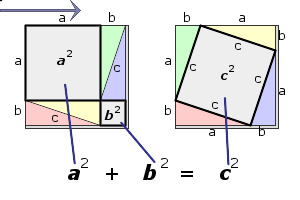
以面积减算法证明

此证明以图形重新排列证明。两个大正方形的面积皆为 ( a + b ) 2 {\displaystyle (a+b)^{2}} 。把四个相等的三角形移除后，左方余下面积为 a 2 + b 2 {\displaystyle a^{2}+b^{2}} ，右方余下面积为 c 2 {\displaystyle c^{2}} ，两者相等。证毕。

以重新排列法证明

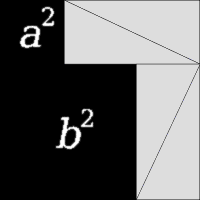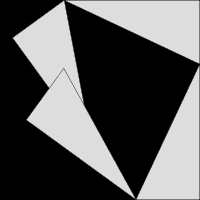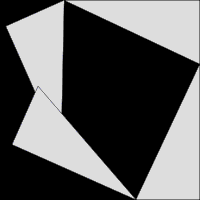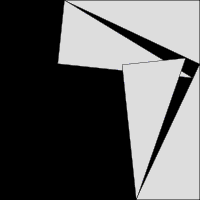
以动画方式来论证勾股定理

勾股定理的逆定理

勾股定理的逆定理是判断三角形为钝角、锐角或直角的一个简单的方法，其中 AB=c为最长边 :

如果 a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}\,} ，则△ABC是直角三角形。

如果 a 2 + b 2 > c 2 {\displaystyle a^{2}+b^{2}>c^{2}\,} ，则△ABC是锐角三角形（若无先前条件AB=c为最长边，则该式的成立仅满足∠C是锐角）。

如果 a 2 + b 2 < c 2 {\displaystyle a^{2}+b^{2} ，则△ABC是钝角三角形。

（这个逆定理其实只是余弦定理的一个延伸）

逆定理的证明

勾股定理的逆定理的证法数明显少于勾股定理的证法。以下是一些常见证法。

同一法

构造 △ △ --> A ′ B ′ C ′ {\displaystyle \triangle A"B"C"} ，使 a ′ = a , b ′ = b , ∠ ∠ --> C ′ = 90 o {\displaystyle a"=a,b"=b,\angle C"=90^{\operatorname {\mathrm {o} } }} 。

根据勾股定理， c ′ = a ′ 2 + b ′ 2 = a 2 + b 2 = c {\displaystyle c"={\sqrt {a"^{2}+b"^{2}}}={\sqrt {a^{2}+b^{2}}}=c} ，从而 △ △ --> A ′ B ′ C ′ ≅ ≅ --> △ △ --> A B C {\displaystyle \triangle A"B"C"\cong \triangle ABC} （SSS）。

因此， ∠ ∠ --> C = 90 o {\displaystyle \angle C=90^{\operatorname {\mathrm {o} } }} 。

余弦定理

根据余弦定理， cos ⁡ ⁡ --> C = a 2 + b 2 − − --> c 2 2 a b {\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}} 。由于 a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}\,} ，故 cos ⁡ ⁡ --> C = 0 {\displaystyle \cos C=0\,} ，从而 ∠ ∠ --> C = 90 o {\displaystyle \angle C=90^{\operatorname {\mathrm {o} } }} 。

相似三角形

在AB边上截取点D使 ∠ ∠ --> D C B = ∠ ∠ --> A {\displaystyle \angle DCB=\angle A} 。

在 △ △ --> C D B {\displaystyle \triangle CDB\,} 与 △ △ --> A C B {\displaystyle \triangle ACB\,} 中， ∠ ∠ --> B = ∠ ∠ --> B , ∠ ∠ --> D C B = ∠ ∠ --> A ⇒ ⇒ --> △ △ --> C D B ∼ ∼ --> △ △ --> A C B {\displaystyle \angle B=\angle B,\angle DCB=\angle A\Rightarrow \triangle CDB\sim \triangle ACB} 。

从而， B C B A = B D B C ⇒ ⇒ --> B D = a 2 c {\displaystyle {\frac {BC}{BA}}={\frac {BD}{BC}}\Rightarrow BD={\frac {a^{2}}{c}}} ，以及 C D A C = C B A B ⇒ ⇒ --> C D = a b c {\displaystyle {\frac {CD}{AC}}={\frac {CB}{AB}}\Rightarrow CD={\frac {ab}{c}}} 。

另一方面， A D = A B − − --> B D = c − − --> a 2 c = b 2 c {\displaystyle AD=AB-BD=c-{\frac {a^{2}}{c}}={\frac {b^{2}}{c}}} ，故由 D C A D = B C A C = B D C D = a b {\displaystyle {\frac {DC}{AD}}={\frac {BC}{AC}}={\frac {BD}{CD}}={\frac {a}{b}}} 知， △ △ --> A C D ∼ ∼ --> △ △ --> C B D {\displaystyle \triangle ACD\sim \triangle CBD} 。

因而， ∠ ∠ --> B D C = ∠ ∠ --> C D A = 90 o {\displaystyle \angle BDC=\angle CDA=90^{\operatorname {\mathrm {o} } }} ，所以 ∠ ∠ --> A C B = ∠ ∠ --> C D B = 90 o {\displaystyle \angle ACB=\angle CDB=90^{\operatorname {\mathrm {o} } }} 。

非欧几何

勾股定理是由欧几里得几何的公理推导出来的，其在非欧几里得几何中是不成立的 。因为勾股定理的成立涉及到了平行公设。

参见

直角三角形

勾股数

余弦定理

青朱出入图

《史记·夏本纪》记载大禹治水：“陆行乘车，水行乘船，泥行乘橇，山行乘檋。左准绳，右规矩，载四时，以开九州，通九道，陂九泽，度九山。”其中的规和矩就是运用勾股定理的实用工具之一。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。