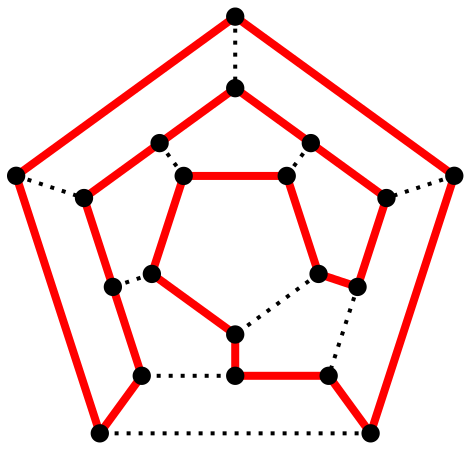
哈密顿图(英语:Hamiltonian path,或Traceable path)是一个无向图,由天文学家哈密顿提出,由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶的路径称作哈密顿路径。
哈密尔顿图的定义: G=(V,E)是一个图,若G中一条通路通过每一个顶点一次且仅一次,称这条通路为哈密尔顿通路。若G中一个圈通过每一个顶点一次且仅一次,称这个圈为哈密尔顿圈。若一个图存在哈密尔顿圈,就称为哈密尔顿图。
哈密尔顿图的必要条件: 若G=(V,E) 是一个哈密尔顿图,则对于V的每一个非空子集S,均有W(G-S) ≤|S|其中W(G-S)表示图G擦去属于S中的顶点后,剩下子图的连通分枝的个数。
哈密尔顿图的充分条件: 设G=(V,E)是一个无向简单图,|V|=n. n≥3. 若对于任意的两个顶点u,v∊V,d(u)+d(v) ≥n,那么, G是哈密尔顿图 。
美国图论数学家...