搜索
很遗憾,我们暂时没有找到您想要的族谱。
试试这些方法:
1.如果您知道堂号或者始祖姓名,可以尝试输入进行检索。
2.我们的客服团队随时准备为您提供支持,您可以点击首页的微信客服获取更多帮助哦!
1.如果您知道堂号或者始祖姓名,可以尝试输入进行检索。
2.我们的客服团队随时准备为您提供支持,您可以点击首页的微信客服获取更多帮助哦!

清空全部

暂无内容
柯姓氏族族谱概况
更多柯姓知识>>
柯
姓氏排名:第157位。位于靳姓之后,梅姓之前。
人口数约:110万
出自姬姓,始成于春秋。黄帝后裔仲雍的五代孙吴国国王名叫相,因与诸侯会盟柯山,故号柯相。吴国柯卢是柯相的曾孙。他的后代遂以"柯"字承接作为自己的姓氏,遂成柯姓。
中华谱库 -“湖南地区,柯氏族谱”
共收录了0本家族宗谱可查

柯氏寻根
克里斯·柯克兰
生平柯克兰早于1987年加盟英冠球会考文垂当学徒球员,在1999年首次替考文垂城在联赛杯对灿美尔的比赛中正选上阵。在2000-01年球季里,由于当时考文垂城正选守门员希特文经常受伤,令柯克兰时常获得上阵机会,其中在当季作客利物浦的联赛中,最后考文垂城落败,不过柯克兰就获得当时的利物浦领队霍利尔赏识。于2001-02年球季柯克兰以600万英镑转会费改投英超老牌球会利物浦。及后获得英格兰U21领队的注意,于2003年获得前英格兰国家足球队领队艾历臣提升为国家队二号守门员,不过只是列入英格兰大军名单,作为两位正选门将詹姆斯及保罗·罗宾逊的替补。直至英格兰国家足球队领队转为麦卡伦后,才在2006年8月对希腊的友赛中才首次为国家队上阵。而柯克兰首次代表国家队上阵也引起了英国媒体的关注。柯克兰的父亲曾在1994年即柯克兰13岁时在博彩公司下注100英镑,以1赔100的赔率赌柯克兰能在30岁前作为英格兰...
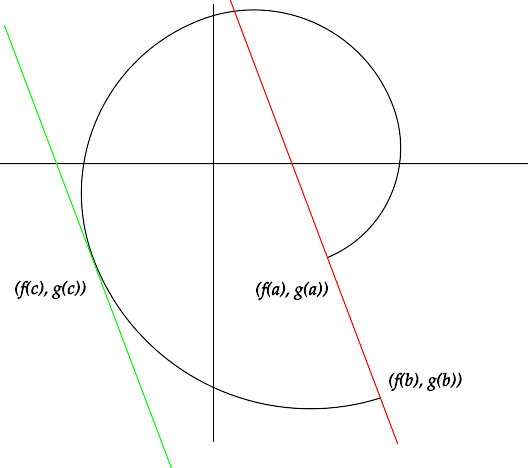
柯西中值定理
内容如果函数f(x){\displaystylef(x)}及g(x){\displaystyleg(x)}满足在闭区间[a,b]{\displaystyle[a,b]}上连续;在开区间(a,b){\displaystyle(a,b)}内可导,对任意x∈∈-->(a,b),g′(x)≠≠-->0{\displaystylex\in(a,b),g"(x)\neq0},那么在(a,b){\displaystyle(a,b)}内至少有一点ξξ-->(a<b){\displaystyle\xi(a使等式柯西定理的几何意义成立。其几何意义为:用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。但柯西定理不能表明在任何情况下不同的两点(f(a),g(a))和(f(b),g(b))都存在切线,因为可能存在一些c值使f′(c)=g′(c)=0,换句话说取某个值时位于曲线的...
奥姆斯柯克
历史Ormskirk一词起源自古诺尔斯语的Ormreskirkja,由蛇或欧洲龙及教堂两词组成。原先可能是维京人聚居地,后来这些维京人皈依基督教。1086年的《末日审判书》中并没有提及奥姆斯柯克,不过据信当时应该是莱瑟姆的一部分。1189年莱瑟姆勋爵将奥姆斯柯克赐予伯思格夫修道院。现奥姆斯柯克市中心的集市本是去往普雷斯顿、利物浦和威根的大路交叉处,原先一直矗立着市场十字架。19世纪时被钟塔替代。该集市是由爱德华一世在1286年颁布皇家宪章而建立的。1292年星期四成为集市日,现在集市日还包括每周的星期六。本来与此同时爱德华一世还赐予了其自治市镇地位,但15世纪末此地失去此头衔,因而又变回普通的镇。1837年济贫法联盟在奥姆斯柯克成立,1853年在当地的威根路(WiganRoad)成立济贫院,后来变成了奥姆斯柯克地区综合医院。地理奥姆斯柯克位于山地斜坡上,最高点海拔68米(223英尺),处在
柯罗诺斯
神话在俄耳普斯的宇宙进化论中,永恒的柯罗诺斯创造出了埃忒尔和卡俄斯,并在神圣的埃忒耳体内做出了一个银色的蛋。这个蛋中孕育出了双性神法涅斯,法涅斯出现的时候,也使一切都出现,法涅斯生出了第一代神祇,他同时也是宇宙的终极创造者。有关柯罗诺斯与克洛诺斯有人把克洛诺斯(Kronos)等同于第一无二的因,因为在所有众神中,他是共有(indivis)、单一(uniel)、父亲和创造善福者。这些人都错了。事实上,他只不过与“第一因”相似:俄耳甫斯把第一因称做柯罗诺斯(Chronos)。两个名字近乎相同。所有先于乌拉诺斯的存在,直至第一因,都被赋予了专有名词。至于那超越心智单子、无法言说的存在,则被称为柯罗诺斯(Chronos),俄耳甫斯以此教示我们,要么这就是繁衍的在先之因,要么真实之在也就是生成之在(devenants),由此揭示了这些存在的法则,以及普遍之于个体的优先性。这样一来,历时逻辑(chro...
柯西积分定理
定理设ΩΩ-->{\displaystyle\Omega}是复平面C{\displaystyle\mathbb{C}}的一个单连通的开子集。f:ΩΩ-->→→-->C{\displaystylef\;:\;\Omega\;\rightarrow\;\mathbb{C}}是一个ΩΩ-->{\displaystyle\Omega}上的全纯函数。设γγ-->{\displaystyle\gamma}是ΩΩ-->{\displaystyle\Omega}内的一个分段可求长的简单闭曲线(即连续而不自交并且能定义长度的闭合曲线),那么:单连通条件的必要性ΩΩ-->{\displaystyle\Omega}是单连通表示ΩΩ-->{\displaystyle\Omega}中没有“洞”,例如任何一个开圆盘D={z:|z−−-->z0|<r}{\di...
电子族谱荐读














