阻力-族谱新闻-族谱网

阻力

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:2244次

转发:0次

评论:0

分类阻力一般可以分为以下几类：寄生阻力（parasiticdrag），包括诱导阻力（lift-induceddrag，只出现在可产生升力的机翼面上）及波动阻力（wavedrag,waveresistance）对于高速（或高雷诺数）的流场而言，一物体的阻力的特性可以用一个无因次的阻力系数来描述，配合阻力系数，可以用阻力方程式来计算阻力。若阻力系数为一常数，阻力约和相对速度的平方成正比，因此需克服阻力需要的功率则和速度的立方成正比。高速时的阻力NASA对阻力的解说阻力方程式可计算物体在较高速（雷诺数Re>~1000）流体下的阻力，此阻力也称为二次阻力或平方阻力。此方程式是由瑞利勋爵所提出，提出时用L（L代表某特定长度）代替A，物体所受的流体阻力如下：其中参考面积A一般定义为物体在运动方向上的正交投影面积。对于形状简单的物体（例如球），参考面即为截面。有时会使用其他的参考面积来定义一物体的阻力系...

分类

阻力一般可以分为以下几类：

寄生阻力（parasitic drag），包括

诱导阻力（lift-induced drag，只出现在可产生升力的机翼面上）及

波动阻力（wave drag, wave resistance）

对于高速（或高雷诺数）的流场而言，一物体的阻力的特性可以用一个无因次的阻力系数来描述，配合阻力系数，可以用阻力方程式来计算阻力。若阻力系数为一常数，阻力约和相对速度的平方成正比，因此需克服阻力需要的功率则和速度的立方成正比。

高速时的阻力

NASA对阻力的解说

阻力方程式可计算物体在较高速（雷诺数Re > ~1000）流体下的阻力，此阻力也称为二次阻力或平方阻力。此方程式是由瑞利勋爵所提出，提出时用L（L代表某特定长度）代替A，物体所受的流体阻力如下：

其中

参考面积A一般定义为物体在运动方向上的正交投影面积。对于形状简单的物体（例如球），参考面即为截面。有时会使用其他的参考面积来定义一物体的阻力系数，此时需特别标明使用的参考面。

以机翼而言，若阻力及升力使用的参考面积相同，阻力及升力的比值（升阻比）即为阻力系数及升力系数（英语：lift coefficient）的比值，在比较阻力及升力的大小时最为方便。因此机翼阻力系数的参考面积一般会是机翼的翼面积（即机翼沿垂直方向的投影面积），而不是沿飞行方向的投影面积。

若物体有光滑的表面，在流场中没有固定的分离点（例如球或圆柱），其阻力系数会随着雷诺数Re而变化，甚至在雷诺数很高（其量级到10）时也是如此。若物体有在流场中有固定的分离点（例如一法向量和流场方向平行的圆盘），在雷诺数Re > 3,500时，阻力系数不随雷诺数而变化。若物体对称球对称，阻力系数也是流场和物体本身对称轴夹角的函数。

自由落体的速度

一物体在在时间t = 0时的初速v = 0，在非浓稠的介质落下（因此不考虑介质的浮力），其速度可以用以下的双曲函数表示：

在t很大时，双曲正切函数tanh其函数极限值为1，因此上述的速度有一渐近值，称为终端速度vt：

对于形状接近球形、平均半径为d、密度为ρobj的物体，终端速度约为

若物体的密度接近水（如雨滴、冰雹、鸟、昆虫等）差不多，在接近海平面的地表落下，终端速度约为

其中

例如人体（d{\displaystyle \mathbf {} d} ~ 0.6 m）其vt{\displaystyle \mathbf {} v_{t}} 约为 70 m/s，体型接近猫的动物（d{\displaystyle \mathbf {} d} ~ 0.2 m）其vt{\displaystyle \mathbf {} v_{t}} 约为 40 m/s，小鸟（d{\displaystyle \mathbf {} d} ~ 0.05 m）其vt{\displaystyle \mathbf {} v_{t}} ~ 20 m/s约为 40 m/s，而昆虫（d{\displaystyle \mathbf {} d} ~ 0.01 m）其vt{\displaystyle \mathbf {} v_{t}} ~ 9 m/s。

非常小的物体（例如花粉）在低雷诺数流体中的终端速度可以用斯托克斯定律来描述。

较大的生物其终端速度较高，因此从高处落下时致命的可能性也较高。例如老鼠和人分别以各自的终端速度坠落时，老鼠其存活的可能性会比人高很多。若蚱蜢以其终端速度坠落时，可能甚至不会受伤。生物大小和其终端速度的关系，以及其肢体截面积和身体质量间的比例关系（一般称为平方立方定律（英语：Square-cube law））可用来说明为何有些小动物从高处落下时不会受伤。

雷诺数很低时的阻力

三个由相同角度（70°）射出物体的轨迹。黑色物体未受到任何阻力，其轨迹为抛物线，蓝色物体受到斯托克斯阻力，而绿色物体受到牛顿阻力。

当物体在雷诺数很低，没有紊流（雷诺数Re<1{\displaystyle R_{e}<1}）的流体中移动时，其受到的阻力称为黏滞阻力、线性阻力。此情形下，阻力大约和速度成正比，但和速度方向相反。黏滞阻力的方程式如下：

其中：

若一物体由静止状态落下，其速度为

其速度会趋近终端速度vt=(ρ ρ -->− − -->ρ ρ -->0)Vgb{\displaystyle \mathbf {} v_{t}={\frac {(\rho -\rho _{0})Vg}{b}}}。若b{\displaystyle \mathbf {} b}为定值，较重的物体会较快落下。

对于小的球形物体缓慢的通过黏性流体（因此雷诺数很小）的情形，斯托克斯推导其阻力常数如下

其中

例如，考虑一半径 r{\displaystyle \mathbf {} r} = 0.5 微米（直径=1.0 µm）的球形物体以10 µm/s的速度通过水中。依上式可得其阻力为0.09 pN，这也就是细菌游过水中所受到的阻力。

空气动力学中的阻力

诱导阻力

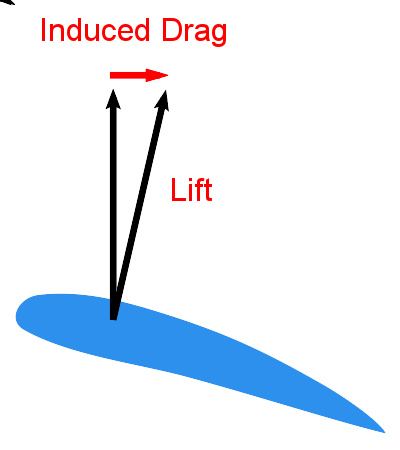
诱导阻力和升力的关系

诱导阻力（或称感应阻力）是指飞行体在产生升力时，一并衍生的阻力。诱导阻力包括二个主要组成成分，一个是因为涡流而产生的阻力（涡流阻力），另一个则是额外产生的黏滞阻力。在飞行体通过空气时，其上表面及下表面的气流压强不同，但在飞行体尾端，上方及下方不同压强的气流会混合，产生紊流及涡流。

在其他参数不变的条件下，当飞行体产生的升力增加时，其诱导阻力也随之增加。对飞行中的飞机而言，这表示在飞机失速前，当其攻角及升力系数（英语：lift coefficient）增加时，其诱导阻力也随之增加。当失速时，升力及诱导阻力都突然下降，而此时飞行体表面形成独立的紊流，造成寄生阻力中的黏滞压差阻力上升

寄生阻力

寄生阻力是一物体在一不可压缩流体中移动所受到的阻力。寄生阻力中包括由秥滞力产生压强差的阻力（形状阻力）以及因表面粗糙度产生的阻力（表面摩擦阻力）。若物体附近有其他相邻近的物体，会产生干扰阻力，有时也会视为寄生阻力的一部分。

在低速飞行时，由于维持升力需要的功率较大，飞机的攻角较大，其产生的诱导阻力也较大。不过当速度提高时诱导阻力随之下降，而流体相对物体的速度提高，因此寄生阻力会变大。若速度已到达穿音速，波动阻力也随之出现。其中速度提高时，诱导阻力下降，其他阻力却随之上升，因此总阻力会在某一速度时出现最小值，若飞机以此速度航行，其效率会等于或接近其最佳效率。飞行员会以此速度来使续航力最大化（使油耗最小化），或是在引撃故障时可以使滑翔距离最大化。

飞行时的功率曲线

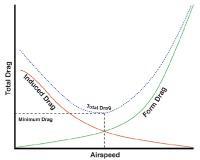
功率曲线：寄生阻力及诱导阻力和速度之间的关系

可以将寄生阻力及诱导阻力相对速度的特性曲线绘制在同一图上，此图在航空学中称为功率曲线。功率曲线可以让飞行员了解不同速度下，飞机飞行所需要输出的功率，是非常重要的曲线。

功率曲线中寄生阻力及诱导阻力有一交点，交点处的阻力总和最小。交点的右侧为正常控制区，当速度越高时，维持定速需要的推力越大。交点的左侧为反向控制区，此区域的功率特性恰好与一般直觉的认知相反：当速度越低时，维持定速需要的推力越大。夂当速度越高时，维持定速需要的推力越大。若飞机的速度低于此交点对应的速度，会出现一个不符合人类直觉的特性：当速度越低时，维持定速需要的推力越大。

跨音速及超音速的波动阻力

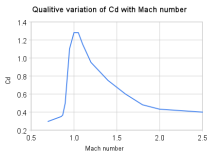
阻力系数与音速的关系示意图

波动阻力（压缩性阻力）是指一高速物体通过可压缩流体时所出现的阻力。在空气动力学中，依飞行速度的不同，波动阻力也可分为几种不同的组成成分。

在跨音速飞行（马赫数介于0.8及1.4之间）时，波动阻力是飞行体形成激波后的结果。一般会出现在出现局部超音速流（局部流体马赫数大于1.0）的区域。实务上，当飞行体较音速低很多，但加速时部分区域的空气速度超过音速，就会出现局部超音速流。因此飞机附近的气流既有超音速流，也有低于音速的亚音速。飞机在跨音速飞行的正常运作过程中常会产生波动阻力，这种波动阻力常称为跨音速压缩性阻力。当马赫数接近1时，跨音速压缩性阻力会显著的上升，远大于同速度下的其他阻力。

在超音速飞行（马赫数大于1.0）时，会在飞行体的前缘及后缘出现斜激波。若速度非常高，或是飞行体转弯角度够大时，则会出现舷波（bow wave）。在超音速飞行时，阻力一般可以分为二个成分：超音速升力相关的波动阻力，及超音速体积相关的波动阻力。

布斯曼双翼机（英语：Busemann"s Biplane）是一种特殊型式的飞行体，当依其设计速度航行时，完全不产生波动阻力，不过它本身无法产生升力。

达朗伯特悖论

位流理论是18世纪最能解释非黏性流的理论。但1752年时法国物理学家达朗伯特依位流理论，推导到位流下其阻力为零的结果，此结果和实测结果矛盾，因此称为达朗伯特悖论（英语：D"Alembert"s_paradox）。

19世纪时科学家圣维南、纳维、斯托克斯开始用纳维－斯托克斯方程来分析黏性流。斯托克斯推导了一球形物体在雷诺数很低的流体中的阻力，其结果即为斯托克斯定律。

纳维－斯托克斯方程在高雷诺数时会趋近非黏性流的欧拉方程式，此时可以用位流理论进行分析，得到阻力为零的结果，但所有在高雷诺数下进行的实验，均证实阻力的存在，和位流所得的结果矛盾。科学家也试着找出除了位流以外，欧拉方程在非黏性定常流的解，不过没有什么进展。

1904年德国科学家普朗特依理论及实验的结果，提出了边界层的概念，也说明了高雷诺数流体为何会产生阻力。