纯态与混合态

假设一个量子系统的量子态是纯态，则这量子态可以用态矢量表示为 | ψ ψ --> ⟩ ⟩ --> {\displaystyle |\psi \rangle } 。几种纯态依照概率组成的量子态称为混合态。例如，假设一个量子系统处于纯态 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 的概率都为50%，则这量子系统处于混合态。密度矩阵专门用来表示混合态。任何量子态，不管是纯态，还是混合态，都可以用密度矩阵表示。

混合态与叠加态的概念不同，几种纯态通过量子叠加所组成的叠加态仍旧是纯态。例如， ( | ψ ψ --> 1 ⟩ ⟩ --> + | ψ ψ --> 2 ⟩ ⟩ --> ) / 2 {\displaystyle (|\psi _{1}\rangle +|\psi _{2}\rangle )/{\sqrt {2}}} 是个纯态。

光子偏振案例

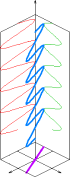
平面偏振

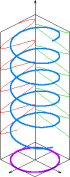
圆偏振

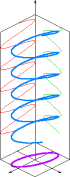
椭圆偏振 平面偏振（紫色）光波的电场（蓝色）可以分解为两个相互垂直的分量（红色与绿色）。

光子的两种圆偏振态，右旋圆偏振态与左旋圆偏振态，分别以态矢量 | R ⟩ ⟩ --> {\displaystyle |R\rangle } 、 | L ⟩ ⟩ --> {\displaystyle |L\rangle } 标记。光子也可能处于叠加态，例如，垂直偏振态与水平偏振态分别为 ( | R ⟩ ⟩ --> + | L ⟩ ⟩ --> ) / 2 {\displaystyle (|R\rangle +|L\rangle )/{\sqrt {2}}} 、 ( | R ⟩ ⟩ --> − − --> | L ⟩ ⟩ --> ) / 2 {\displaystyle (|R\rangle -|L\rangle )/{\sqrt {2}}} 。更一般地，光子偏振所处于的叠加态可以表示为 α α --> | R ⟩ ⟩ --> + β β --> | L ⟩ ⟩ --> {\displaystyle \alpha |R\rangle +\beta |L\rangle } ；其中， α α --> {\displaystyle \alpha } 、 β β --> {\displaystyle \beta } 是系数。这一般式可以表示平面偏振态、圆偏振态、椭圆偏振态等等。

假若让处于叠加态 ( | R ⟩ ⟩ --> + | L ⟩ ⟩ --> ) / 2 {\displaystyle (|R\rangle +|L\rangle )/{\sqrt {2}}} 的光子通过左旋圆偏振器，则出射的光子处于左旋圆偏振态 | L ⟩ ⟩ --> {\displaystyle |L\rangle } ；假若通过右旋圆偏振器，则出射的光子处于右旋圆偏振态 | R ⟩ ⟩ --> {\displaystyle |R\rangle } 。强度这两种圆偏振模，光子强度都会减半，貌似意味着叠加态 ( | R ⟩ ⟩ --> + | L ⟩ ⟩ --> ) / 2 {\displaystyle (|R\rangle +|L\rangle )/{\sqrt {2}}} 的一半光子处于量子态 | R ⟩ ⟩ --> {\displaystyle |R\rangle } ，另一半处于量子态 | L ⟩ ⟩ --> {\displaystyle |L\rangle } ，但这种解释并不正确，处于量子态 | R ⟩ ⟩ --> {\displaystyle |R\rangle } 与 | L ⟩ ⟩ --> {\displaystyle |L\rangle } 的光子都有可能被垂直平面偏振器吸收，但是处于量子态 ( | R ⟩ ⟩ --> + | L ⟩ ⟩ --> ) / 2 {\displaystyle (|R\rangle +|L\rangle )/{\sqrt {2}}} 的光子不会被垂直平面偏振器吸收。

从白炽灯发射出的光子是一种非偏振态光子，不能用叠加态 α α --> | R ⟩ ⟩ --> + β β --> | L ⟩ ⟩ --> {\displaystyle \alpha |R\rangle +\beta |L\rangle } 来描述。特别而言，与平面偏振态光子不同，它通过任何偏振器后都会失去50%强度，与圆偏振态光子不同，使用波片（waveplate）不能直接将它改变为平面偏振态光子。非偏振态光子可以描述为，处于 | R ⟩ ⟩ --> {\displaystyle |R\rangle } 的概率是50%，处于 | L ⟩ ⟩ --> {\displaystyle |L\rangle } 的概率是50%。它也可以描述为，处于垂值偏振态的概率是50%，处于水平偏振态的概率是50%。

非偏振态光子的量子态不是纯态，而是由几种纯态依照统计概率组成。它可以由50%右旋圆偏振态与50%左旋圆偏振态组成，或者，它可以由50%垂直偏振态与50%水平偏振态组成。这两种组合无法做实验辨识区分，因此它们被视为同样的混合态。密度算符含有混合态的所有资料，足够计算任何关于混合态的可测量性质。

混合态到底源自何处？试想非偏振态光子是怎样制成的。一种方法是利用处于动力学平衡的系统，这系统拥有很多个微观态（microstate），伴随每一个微观态都有其发生的概率（玻尔兹曼因子），它们会因热力学涨落（thermal fluctuation）从一个微观态变换到另一个微观态。热力学随机性可以解释白炽灯怎样发射非偏振光子。另一种方法是引入不确定性于系统的制备程序，例如，将光束通过表面粗糙的双折射晶体，使得光束的不同部分获得不同偏振。第三种方法应用EPR机制，有些放射性衰变会发射两个光子朝着反方向移动离开，这纠缠系统的量子态为 ( | R , L ⟩ ⟩ --> + | L , R ⟩ ⟩ --> ) / 2 {\displaystyle (|R,L\rangle +|L,R\rangle )/{\sqrt {2}}} ，整个系统是处于纯态，但是每一个光子子系统的物理行为如同非偏振态光子，从分析光子子系统的约化密度算符，可以得到这结论。

一般而言，混合态时常会出现于几种纯态的统计性混合（例如热力学平衡）、制备程序的不确定性（例如光子可能移动于稍微不同路径）、包含在纠缠系统内的子系统（例如EPR机制）。

数学表述

纯态

假设一个量子系统的量子态是纯态，则这量子态可以用态矢量表示为 | ψ ψ --> ⟩ ⟩ --> {\displaystyle |\psi \rangle } ，对应的密度算符定义为

从密度算符的形式，可以推论密度算符是自伴算符：

假设，物理量 A {\displaystyle A} 是这量子系统的可观察量，其本征值为 a i {\displaystyle a_{i}} 的本征态 | a i ⟩ ⟩ --> , i = 1 , 2 , 3 , ⋯ ⋯ --> , n {\displaystyle |a_{i}\rangle ,\quad i=1,\ 2,\ 3,\ \cdots ,n} 形成一个规范正交基 { | a i ⟩ ⟩ --> } {\displaystyle \{|a_{i}\rangle \}} ，则对可观察量 A {\displaystyle A} 做测量得到 a i {\displaystyle a_{i}} 的概率 P ( a i ) {\displaystyle {\mathcal {P}}(a_{i})} 为

其中， Λ Λ --> ( a i ) = d e f | a i ⟩ ⟩ --> ⟨ ⟨ --> a i | {\displaystyle \Lambda (a_{i})\ {\stackrel {def}{=}}\ |a_{i}\rangle \langle a_{i}|} 是对应于本征态 | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 的投影算符， tr ( ) {\displaystyle {\hbox{tr}}()} 是迹数。

做实验测量可观察量 A {\displaystyle A} 获得的期望值为

这种可观察量的期望值与迹数运算之间的关系称为迹定则（trace rule）。 对于不同的规范正交基，迹数是个不变量。采用任何规范正交基，都可以计算出同样迹数。 另外，概率公式与期望值公式对于密度算符都具有线性，这是很优良的性质，这意味着概率公式与期望值公式也适用于几个密度算符的线性组合。

由于 | ψ ψ --> ⟩ ⟩ --> {\displaystyle |\psi \rangle } 被归一化， 密度算符的迹数为1：

对于任意归一化量子态 ϕ ϕ --> {\displaystyle \phi } ，

所以，密度算符是非负算符（nonnegative operator）。

混合态

将先前纯态密度算符的定义式加以延伸，假设在一个量子系统处于纯态 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 、 | ψ ψ --> 3 ⟩ ⟩ --> {\displaystyle |\psi _{3}\rangle } 、……的概率分别为 w 1 {\displaystyle w_{1}} 、 w 2 {\displaystyle w_{2}} 、 w 3 {\displaystyle w_{3}} 、……，则这混合态量子系统的密度算符 ρ ρ --> {\displaystyle \rho } 为

每一个概率都是非负实值，所有概率的总和为1：

按照“无知诠释”，这种量子系统确定是处于某个纯态 ψ ψ --> i {\displaystyle \psi _{i}} ，但是无法知道到底是哪一个纯态。这种可以用无知诠释来论述的量子系统称为“真混合物”（proper mixture），否则，称为“瑕混合物”（improper mixture）。

回想在纯态段落里，概率公式与期望值公式对于密度算符都具有线性，这意味着对于混合态的密度算符，这些公式也都适用。加以延伸后的密度算符，也具有先前纯态的密度算符所拥有的性质：

密度算符是自伴算符： ρ ρ --> = ρ ρ --> † † --> {\displaystyle \rho =\rho ^{\dagger }} 。

密度算符的迹数为1： tr ( ρ ρ --> ) = 1 {\displaystyle {\hbox{tr}}(\rho )=1} 。

对可观察量 A {\displaystyle A} 做测量得到 a i {\displaystyle a_{i}} 的概率为 P ( a i ) = tr ( Λ Λ --> ( a i ) ρ ρ --> ) {\displaystyle {\mathcal {P}}(a_{i})={\hbox{tr}}(\Lambda (a_{i})\rho )} 。

做实验测量可观察量 A {\displaystyle A} 获得的期望值为 ⟨ ⟨ --> A ⟩ ⟩ --> = tr ( A ρ ρ --> ) {\displaystyle \langle A\rangle ={\hbox{tr}}(A\rho )} 。

密度算符是非负算符： 0 ≤ ≤ --> ⟨ ⟨ --> ϕ ϕ --> | ρ ρ --> | ϕ ϕ --> ⟩ ⟩ --> ≤ ≤ --> 1 {\displaystyle 0\leq \langle \phi |\rho |\phi \rangle \leq 1} 。

由于密度算符 ρ ρ --> {\displaystyle \rho } 是自伴算符，它具有谱表示

其中， | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 是本征值为 a i {\displaystyle a_{i}} 的本征态，所有 | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 形成一个规范正交基。

按照自伴算符的定义，每一个本征值 a i {\displaystyle a_{i}} 是它自己的共轭：

由于密度算符 ρ ρ --> {\displaystyle \rho } 是非负算符，每一个本征值 a i {\displaystyle a_{i}} 都是非负值。

由于密度算符 ρ ρ --> {\displaystyle \rho } 的迹数为1，

给定一个量子系统，其所有可能的密度算符组成一个凸集。假设 ρ ρ --> i , i = 1 , 2 , 3 , . . . , n {\displaystyle \rho _{i},\quad i=1,2,3,...,n} 属于这凸集，则 ρ ρ --> = ∑ ∑ --> i c i ρ ρ --> i {\displaystyle \rho =\sum _{i}c_{i}\rho _{i}} 也属于这凸集；其中， 0 ≤ ≤ --> c i ≤ ≤ --> 1 {\displaystyle 0\leq c_{i}\leq 1} 是系数， ∑ ∑ --> i c i = 1 {\displaystyle \sum _{i}c_{i}=1} 。

用密度算符辨认纯态与混合态

由于纯态的密度算符定义式为

所以纯态的密度算符具有特征

ρ ρ --> 2 = ρ ρ --> {\displaystyle \rho ^{2}=\rho } 。

tr ( ρ ρ --> 2 ) = tr ( ρ ρ --> ) = 1 {\displaystyle {\hbox{tr}}(\rho ^{2})={\hbox{tr}}(\rho )=1} 。

否则，非纯态的密度算符遵守关系式

另外，将纯态的密度矩阵 ϱ ϱ --> {\displaystyle \varrho } 对角化后，只能有一个对角元素等于1，其它对角元素都等于0，例如，一种形式为

量子态的 纯度 （ 英语 ： purity (quantum mechanics) ） γ γ --> {\displaystyle \gamma } 定义为

纯态的纯度为1。处于N维希尔伯特空间、完全混合的混合态，其对角元素的数值为 1 / N {\displaystyle 1/N} 、非对角元素的数值为0，其纯度为 1 / N {\displaystyle 1/N} 。

冯诺伊曼熵是另一种描述量子态混合程度的量度。

连续性本征态基底

位置是一种连续性可观察量，具有连续性本征值谱，用这种可观察量的连续性本征态为基底，密度矩阵 ϱ ϱ --> {\displaystyle \varrho } 含有两个位置参数 x ′ {\displaystyle x"} 、 x ″ {\displaystyle x""} ：

可观察量 A {\displaystyle A} 的期望值为

复合系统

假设密度算符为 ρ ρ --> {\displaystyle \rho } 的复合系统是由两个子系统 A {\displaystyle A} 、 B {\displaystyle B} 组成，这两个子系统的物理行为分别由其对应约化密度算符（reduced density operator） ρ ρ --> A {\displaystyle \rho _{A}} 、 ρ ρ --> B {\displaystyle \rho _{B}} 描述：

其中， tr B {\displaystyle {\hbox{tr}}_{B}} 、 tr A {\displaystyle {\hbox{tr}}_{A}} 分别是对于子系统 B {\displaystyle B} 、 A {\displaystyle A} 的偏迹数（partial trace）。

这复合系统的两个子系统之间没有任何关联（没有任何量子关联或经典关联），当且仅当 ρ ρ --> {\displaystyle \rho } 是 ρ ρ --> A {\displaystyle \rho _{A}} 与 ρ ρ --> B {\displaystyle \rho _{B}} 的张量积：

约化密度算符

约化密度算符的点子最先由保罗·狄拉克于1930年提出 。假设两个希尔伯特空间 H A {\displaystyle H_{A}} 、 H B {\displaystyle H_{B}} 的规范正交基分别为 { | a i ⟩ ⟩ --> A } {\displaystyle \{|a_{i}\rangle _{A}\}} 、 { | b j ⟩ ⟩ --> B } {\displaystyle \{|b_{j}\rangle _{B}\}} ，分别在这两个希尔伯特空间 H A {\displaystyle H_{A}} 、 H B {\displaystyle H_{B}} 的两个子系统 A {\displaystyle A} 、 B {\displaystyle B} 所组成的复合系统，其量子态为纯态 | ψ ψ --> ⟩ ⟩ --> {\displaystyle |\psi \rangle } ，其密度算符 ρ ρ --> {\displaystyle \rho } 为

取密度算符 ρ ρ --> {\displaystyle \rho } 对于子系统 B {\displaystyle B} 的偏迹数，可以得到子系统 A {\displaystyle A} 的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} ：

例如，纠缠态 | ψ ψ --> ⟩ ⟩ --> A B = ( | 0 ⟩ ⟩ --> A ⊗ ⊗ --> | 1 ⟩ ⟩ --> B − − --> | 1 ⟩ ⟩ --> A ⊗ ⊗ --> | 0 ⟩ ⟩ --> B ) / 2 {\displaystyle |\psi \rangle _{AB}=(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B})/{\sqrt {2}}} ，其子系统 A {\displaystyle A} 的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} 为

如同预想，这公式演示出，子系统 A {\displaystyle A} 的约化密度算符 ρ ρ --> A {\displaystyle \rho _{A}} 为混合态。

范例

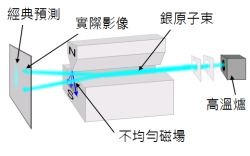
设定施特恩-格拉赫实验仪器的磁场方向为z-轴，入射的银原子束可以被分裂成两道银原子束，每一道银原子束代表一种量子态，上旋 | ↑ ↑ --> ⟩ ⟩ --> {\displaystyle |\uparrow \rangle } 或下旋 | ↓ ↓ --> ⟩ ⟩ --> {\displaystyle |\downarrow \rangle } 。

如右图所示，使用z-轴方向的施特恩-格拉赫实验仪器，可以将入射的银原子束，依照自旋的z-分量 S z {\displaystyle S_{z}} 分裂成两道，一道的 S z {\displaystyle S_{z}} 为上旋，标记为 | z + ⟩ ⟩ --> {\displaystyle |z+\rangle } ，另一道的 S z {\displaystyle S_{z}} 为下旋，标记为 | z − − --> ⟩ ⟩ --> {\displaystyle |z-\rangle } 。

z-轴方向

态矢量： | z + ⟩ ⟩ --> = ( 1 0 ) {\displaystyle |z+\rangle ={\begin{pmatrix}1\\0\end{pmatrix}}} 。

态矢量： | z − − --> ⟩ ⟩ --> = ( 0 1 ) {\displaystyle |z-\rangle ={\begin{pmatrix}0\\1\end{pmatrix}}} 。

x-轴方向

态矢量： | x + ⟩ ⟩ --> = ( 1 2 1 2 ) {\displaystyle |x+\rangle ={\begin{pmatrix}{\frac {1}{\sqrt {2}}}\\{\frac {1}{\sqrt {2}}}\end{pmatrix}}} 。

态矢量： | x − − --> ⟩ ⟩ --> = ( 1 2 − − --> 1 2 ) {\displaystyle |x-\rangle ={\begin{pmatrix}{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}} 。

y-轴方向

态矢量： | y + ⟩ ⟩ --> = ( 1 2 i 2 ) {\displaystyle |y+\rangle ={\begin{pmatrix}{\frac {1}{\sqrt {2}}}\\{\frac {i}{\sqrt {2}}}\end{pmatrix}}} 。

态矢量： | y − − --> ⟩ ⟩ --> = ( 1 2 − − --> i 2 ) {\displaystyle |y-\rangle ={\begin{pmatrix}{\frac {1}{\sqrt {2}}}\\-{\frac {i}{\sqrt {2}}}\end{pmatrix}}} 。

完全随机粒子束

完全随机粒子束的量子态不是纯态，它可以由50% | z + ⟩ ⟩ --> {\displaystyle |z+\rangle } 纯态与50% | z − − --> ⟩ ⟩ --> {\displaystyle |z-\rangle } 纯态组成：

它也可以由50% | x + ⟩ ⟩ --> {\displaystyle |x+\rangle } 纯态与50% | x − − --> ⟩ ⟩ --> {\displaystyle |x-\rangle } 纯态组成：

另外，它还可以由50% | y + ⟩ ⟩ --> {\displaystyle |y+\rangle } 纯态与50% | y − − --> ⟩ ⟩ --> {\displaystyle |y-\rangle } 纯态组成，因此可见，不同的组合仍可得到同样的混合态。

一般而言，完全随机粒子束的 N × × --> N {\displaystyle N\times N} 密度矩阵 ϱ ϱ --> {\displaystyle \varrho } ，经过对角化之后，可以写为

冯诺伊曼方程

薛定谔方程描述纯态怎样随着时间流逝而演化，冯诺伊曼方程描述密度算符怎样随着时间流逝而演化。实际而言，这两种方程等价，因为它们彼此都可以推导出对方。假设，在时间 t 0 {\displaystyle t_{0}} ，量子系统的密度算符为

其中，量子系统在时间 t 0 {\displaystyle t_{0}} 处于纯态 | ψ ψ --> i ( t 0 ) ⟩ ⟩ --> {\displaystyle |\psi _{i}(t_{0})\rangle } 的概率是 w i {\displaystyle w_{i}}

假若不搅扰这量子系统，则概率 w i {\displaystyle w_{i}} 跟时间无关。在时间 t {\displaystyle t} ，纯态 | ψ ψ --> i ( t ) ⟩ ⟩ --> {\displaystyle |\psi _{i}(t)\rangle } 遵守含时薛定谔方程

其中， ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数， H {\displaystyle H} 是哈密顿算符。

所以，冯诺伊曼方程表示为

其中，方括弧代表对易算符。

注意到只有当采用薛定谔绘景时（必须采用薛定谔绘景来计算密度算符）这方程才成立，虽然这方程看起来很像海森堡绘景的海森堡方程，唯一差别是关键的正负号：

其中， A ( H ) {\displaystyle A^{(H)}} 是某种采用海森堡绘景的算符。

在海森堡绘景里，密度算符与时间无关，正负号差别确使期望值 ⟨ ⟨ --> A ⟩ ⟩ --> {\displaystyle \langle A\rangle } 对于时间的导数会得到与薛定谔绘景相同的结果。

假若哈密顿算符不含时，则可从冯诺伊曼方程推导出

冯诺伊曼熵

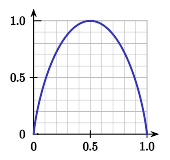
对于两体纯态系统，冯诺伊曼熵 σ σ --> {\displaystyle \sigma } （竖轴）与本征值 a i {\displaystyle a_{i}} （横轴）之间的关系曲线。

在量子统计力学（quantum statistical mechanics）里，冯诺伊曼熵（von Neumann entropy）是经典统计力学关于熵概念的延伸。对于密度矩阵为 ϱ ϱ --> {\displaystyle \varrho } 的混合态，冯诺伊曼熵定义为

这公式涉及到矩阵对数（logarithm of a matrix），似乎很难计算， 但密度算符 ρ ρ --> {\displaystyle \rho } 是自伴算符，具有谱表示

其中， | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 是本征值为 a i {\displaystyle a_{i}} 的本征态，所有 | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 形成一个规范正交基。

因此，可以将密度矩阵 ϱ ϱ --> {\displaystyle \varrho } 对角化，将冯诺伊曼熵更简单地以对角化后的密度矩阵 ϱ ϱ --> {\displaystyle \varrho } 定义为

冯诺伊曼熵 σ σ --> {\displaystyle \sigma } 又可以写为

从这形式，可以推论冯诺伊曼熵与经典信息论里的香农熵（Shannon entropy）相关。

在这里，可以视每一个本征值 a i {\displaystyle a_{i}} 为处于本征态 | a i ⟩ ⟩ --> {\displaystyle |a_{i}\rangle } 的概率。假若某事件的发生概率为零，则这事件不应贡献出丝毫冯诺伊曼熵。从数学而言，以下极限为零：

因此，可以采用约定

纯态的冯诺伊曼熵为零，因为其密度矩阵对角化之后，只有一个元素为1，其它均为0。即所有对角元素 a i {\displaystyle a_{i}} 必定满足 a i = 0 {\displaystyle a_{i}=0} 或 ln ⁡ ⁡ --> a i = 0 {\displaystyle \ln a_{i}=0} 。

完全随机混合态的 N × × --> N {\displaystyle N\times N} 密度矩阵，其冯诺伊曼熵 σ σ --> {\displaystyle \sigma } 为

假若，将冯诺伊曼熵视为量子系统失序现象的一种量度，则纯态拥有最小的冯诺伊曼熵 0 {\displaystyle 0} ，而完全随机混合态拥有最大的冯诺伊曼熵 ln ⁡ ⁡ --> N {\displaystyle \ln N} 。

每一次做投影测量，冯诺伊曼熵都会增加，永远不会减少，但是，对于广义测量（generalized measurement），冯诺伊曼熵可能会减少。 混合态的冯诺伊曼熵永远不小于零。因此，纯态可以通过投影测量改变为混合态，但是，非纯态的混合态永远无法通过投影测量改变为纯态。投影测量这动作促成了一种基本不可逆性的对于密度算符的改变，如同波函数坍缩。实际而言，相当反直觉地，投影测量这动作抹除了复合系统的量子相干性。更详尽内容，请参阅条目量子退相干。

一个量子系统的子系统可以从混合态改变为纯态，但是所附出的代价是其它部分的冯诺伊曼熵会增加，就好似将一个物体放进冰箱来降低其熵，冰箱热交换器外的空气会变暖，而所增加的熵会比物体所减少的熵更多。更详尽内容，请参阅条目热力学第二定律。

参阅

玻恩法则（Born rule）

葛利生定理（Gleason"s theorem）

密度泛函理论

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。