徐积积字仲车，楚州山阳（今江苏淮字）人。生于天圣六年（1028）。治平四年（1067）进士第。除扬州司户参军、楚州教授，改和州防御推官。徽宗立，改宣德郎。崇宁二年（1103）卒，年七十六。政和间，赐谥节孝处士。有集二十卷。

徐积锴，生于1918年，父亲是我国著名诗人徐志摩，母亲张幼仪。现有一子三女，居住在美国。徐积锴13岁时，徐志摩坠机身亡，由母亲抚养成人。他小名叫“阿欢”。由于是徐家单丁独传，全家上下对之都寄予厚望。出世百日，家人在他面前摆了裁缝用量身尺、小算盘、铜钱和一把笔，让他“抓阄”。阿欢看了片刻，眼睛先瞅着算盘，继而扫到尺子，最后盯上一样东西，伸手便抓起——哟，那正是徐志摩用过的毛笔。徐志摩父亲徐申如先生喜出望外，把孙子高高举起，连连道：“又是一个读书人！我们家孙子将来要用铁笔！”这“铁笔”，是指官府重要文告上常用语“铁笔不改”。徐老太爷希望孙子从政入仕（积锴之名亦与此有关），哪里料到，徐积锴后来的生活道路，却与祖父希望大相径庭。徐志摩死后不久，他中学毕业，为便谋生，遂入交通大学念土木工程。1947年徐积锴赴美，在哥伦比亚大学和纽约科技大学攻读经济和土木工程，先为土木工程师，后从商，跟笔墨生涯始终无...

代数对象的积各种代数结构中的对象可以通过定义不同的二元运算得到不同的积。比如说，平面向量可以定义点积，三维向量可以定义叉积和混合积。常见的积还包括：向量空间中两个向量的内积矩阵集合中矩阵的乘积矩阵的阿达马乘积矩阵的克罗内克乘积张量的外积张量的张量积两个函数的逐点乘积代数结构的积在研究抽象代数中的代数结构时，常常会用到代数结构的积的概念。两个代数结构的积，一般定义为将两个代数结构里的元素通过一个二元映射对应为一个新的元素，然后将新的元素通过适当的规则组成的新的代数结构。如果两个代数结构的元素个数都是有限个，那么它们的积的元素个数将会是它们分别元素个数的乘积。这也是这种新代数结构被称为积的原因之一。常见的代数结构的积有：笛卡儿积向量空间的直积群子集的乘积群的自由积拓扑空间的积参考来源

历史勒考特家族瑞士勒考特家族的最早记录可追溯到十六世纪。当时，身为法国胡格诺教徒的皮埃尔•勒考特（PierreLeCoultre，约1530~约1600）为躲避宗教迫害，从法国一个名为Lisy-sur-Ourcq的小村庄，逃到日内瓦。1558年，皮埃尔获得日内瓦“居民”身份，并于次年在汝山谷（ValléedeJoux）获得一块土地。随着时间的流逝，汝山谷逐渐形成一个小型社区。1612年，皮埃尔之子在此地建立一座教堂，勒桑捷村庄从此成立，也即今日积家表厂总部。积家表厂1833年，安东尼•勒考特（AntoineLeCoultre，1803-1881）发明出一种能从钢片车削出钟表齿轮的机具，并随即在勒桑捷成立一家小型制表工坊，集合所有钟表技术来打造各种高品质钟表。1844年，安东尼发明出世界上最精准的测量仪器──微米仪（参见1.4.1章节）。1847年，又研制出“无匙上链”系统，对钟表进行上链与

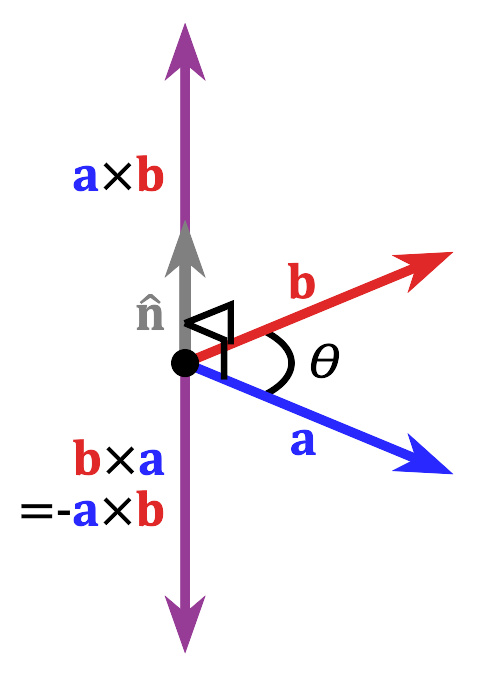
定义在右手坐标系中的向量积两个向量a{\displaystyle\mathbf{a}}和b{\displaystyle\mathbf{b}}的叉积写作a××-->b{\displaystyle\mathbf{a}\times\mathbf{b}}（有时也被写成a∧∧-->b{\displaystyle\mathbf{a}\wedge\mathbf{b}}，避免和字母x混淆）。叉积可以定义为：在这里θθ-->{\displaystyle\theta}表示a{\displaystyle\mathbf{a}}和b{\displaystyle\mathbf{b}}之间的角度（0∘∘-->≤≤-->θθ-->≤≤-->180∘∘-->{\displaystyle0^{\circ}\leq\theta\leq180^{\circ}}），它位于这两个向量所...