发现

威廉·赫歇耳声称他曾经在1789年看见天王星环，并指出该环是红色的。 但是，人们怀疑赫歇耳发现天王星环一事的真确性，全因在随后的两个世纪没有一个观测者曾经注意到环的存在。尽管如此，部分天文学家透过使用凯克天文台望远镜观察，声称他们能够确定了赫歇耳至少发现了ν环。

环确实的发现日期是1977年3月10日，其发现者是使用柯伊伯机载天文台观测的 詹姆斯·勒德洛·埃利奥特 （ 英语 ： James L. Elliot ） 、爱德华·W·邓纳姆和 杰西卡·明基 （ 英语 ： D. J. Mink ） 。这个发现是很意外的，他们原本的计划是观测天王星掩蔽SAO 158687以研究天王星的大气层。 然而，当他们分析观测的资料时，他们发现在行星掩蔽的前后，这颗恒星都曾经短暂的消失了五次。他们认为，天王星必须有个环系统围绕着行星才能解释这个现象。 他们便因此发现了天王星的5个环，并将它们命名为α、β、γ、δ和ε。 稍后，它们又发现了4道较暗的环，其中一个位于β环和γ环之间，而其他三个则位于α环内。 使环的数量增加为9圈。位于β环和γ环之间的环被命名为η，而其余三个环则被命名为4、5和6。 天王星环是人类在太阳系中发现的第二个行星环，仅次于土星环。

天王星环于1986年正式被太空船旅行者2号拍摄。 天文学家们在照片中又找到了两个更薄弱的环，令到环的数量增加为11圈。 哈勃太空望远镜于2003年及2005年先后发现了两个环，令到环的数量增加为13圈。这些外圈的发现令到天王星环系统的半径增加了一倍。 哈勃还同时拍摄了两颗未被发现的天王星小卫星。

一般特性

天王星共有13个环。从内至外，它们是：1986U2R/ζ、6、5、4、α、β、η、γ、δ、λ、ε、ν和μ。 它们可以被分成三组：9个为狭窄主环（6、5、4、α、β、η、γ、δ、ε） ，2个为多尘环（1986U2R/ζ、λ） ，以及两个为外环（μ、ν）。 天王星的环主要是由微粒和尘埃组成 ，例如1986U2R/ζ环、η环、δ环、λ环、ν环和μ环均包含尘埃。 在这些环之间，可能存在着无数的薄灰尘环。 这些微薄环和尘埃带可能只是多个暂时存在的环弧。 旅行者2号是透过正向散射拍摄大部分的灰尘带。

天王星环大多是由极暗的物料组成。天王星环的几何反照率不会超过5–6%，而球面反照率更低：低于2%。 当环的相位角趋向零时，其球面反照率就会增加。 这意味着他们的反照率其实还要低得多。 这些环并不可能像土星环般，由纯冰组成，因为纯冰组成的环将会比天王星内卫星还要暗。 这显示天王星环可能是由冰和深色材料的混合物组成，类似于内卫星的物料。

外环系统

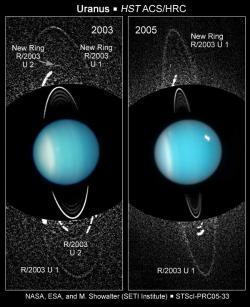
  数位反射下的Mu环和Nu环（R/2003 U 1和U 2）

在2005年12月，哈伯太空望远镜侦测到一对早先未曾发现的圆环，现在称为外环系统，使天王星环已知的数量增加到13圈。最外面的环称为μ环，是较明亮的η环距离的两倍远。哈伯同时也发现了两颗新的小卫星，其中的天卫二十六还与最外面的μ环共享轨道，并且被炸出来的表面物质可能是环的原料来源。 在2006年4月，凯克天文台公布的新环影像中，最外环的一圈是蓝色的，另一圈则是红色的。

关于外环颜色是蓝色的一个假说是，它由来自天卫二十六的细小冰微粒组成，因此能散射足够多的蓝光。 天王星的内环看起来是呈灰色的。

起源

天王星环是相当年轻的，在圆环之间的空隙和混浊度上的差异显示它们不是与天王星同时形成的。在环中的物质可能是一次高速的撞击或是潮汐力扯碎卫星一部分形成的碎片。

赫协尔的观测

部分天文学家认为威廉·赫歇耳是首个发现天王星环的人。认为威廉·赫歇耳在18世纪就观察到天王星环的理由，首先来自于他的观测记录。该记录详述了于1789年2月22日对天王星的观测，并包括以下的段落：“可能有一个环”。

赫歇耳在一张小图上画出了一个圆环，并且注明“有点倾向是红色”。而夏威夷的凯克望远镜则证实了这样的描述是真实的。 赫歇耳的笔记在1797年被皇家学会印制出版，但是在1797至1977年将近二个世纪的时间，天王星环很少，甚至是根本未曾被提及。这让部分天文学家怀疑为什么只有赫歇耳发现了天王星环，而之后其他的数百位天文学家却完全没有发现。另外，即使赫歇耳给了天王星环与天王星大小的正确关系，天王星在太阳附近的移动也可能改变了环和他的颜色。

列表

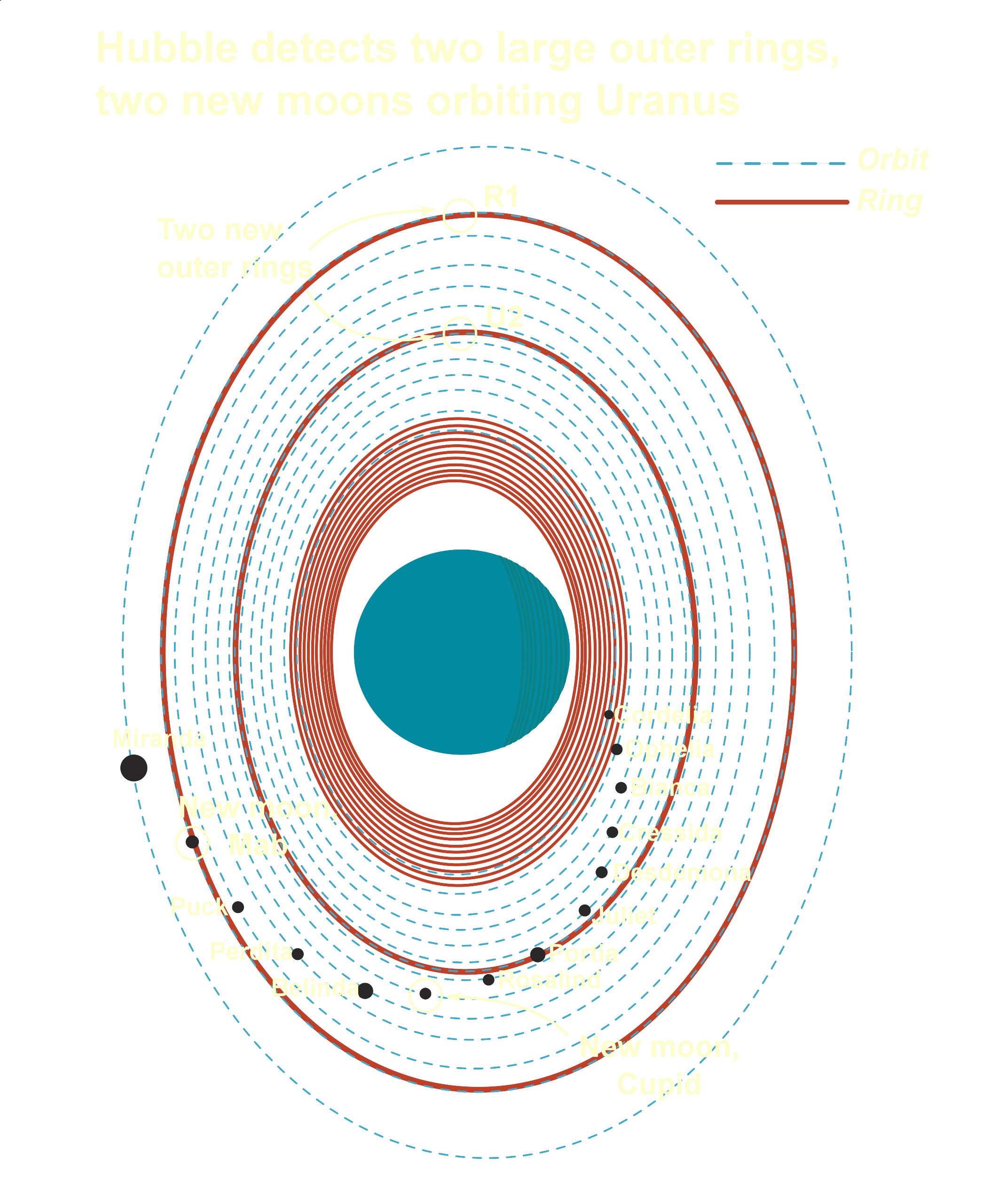
  天王星的卫星和环概要图。

这是天王星的行星环系统摘要总表：

相关条目

土星环

海王星环

木星环

丽亚环

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。