数学表示方法

自然对数的一般表示方法为ln⁡ ⁡ -->x{\displaystyle \ln x\!}。数学中亦有以log⁡ ⁡ -->x{\displaystyle \log x\!}表示自然对数。若要避免常用对数0的常用对数log⁡ ⁡ -->x{\displaystyle \log x\!}混淆，可用“全写”loge⁡ ⁡ -->x{\displaystyle \log _{\boldsymbol {e}}x\!}。

历史

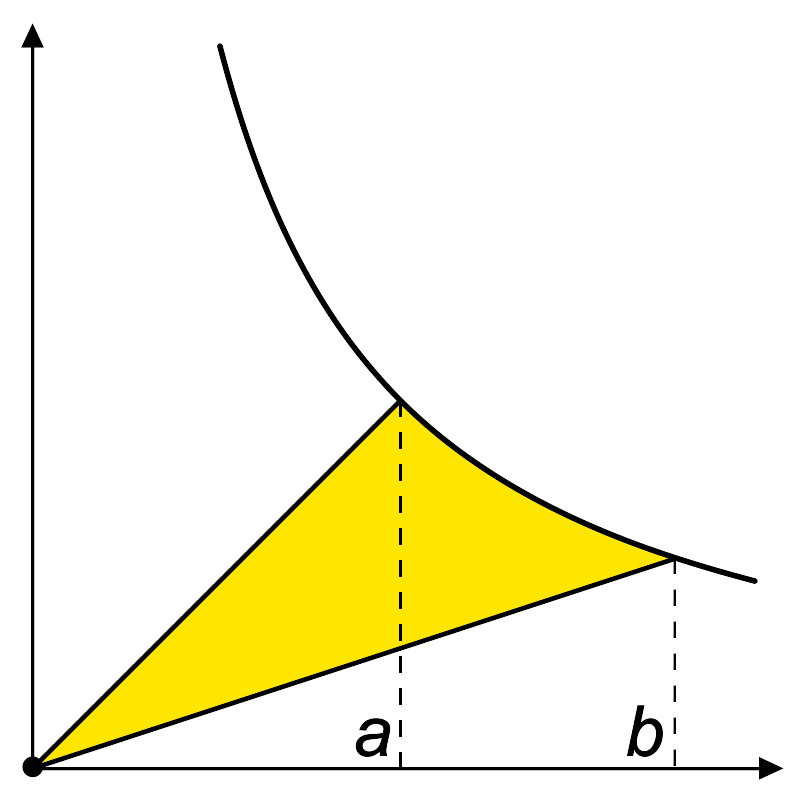
双曲线扇形是笛卡尔平面{(x,y)}上的一个区域，由从原点到(a, 1/a)和(b, 1/b)的射线，以及双曲线xy = 1围成。在标准位置的双曲线扇形有a = 1且b > 1，它的面积为ln(b)，此时双曲线扇形对应正双曲角。

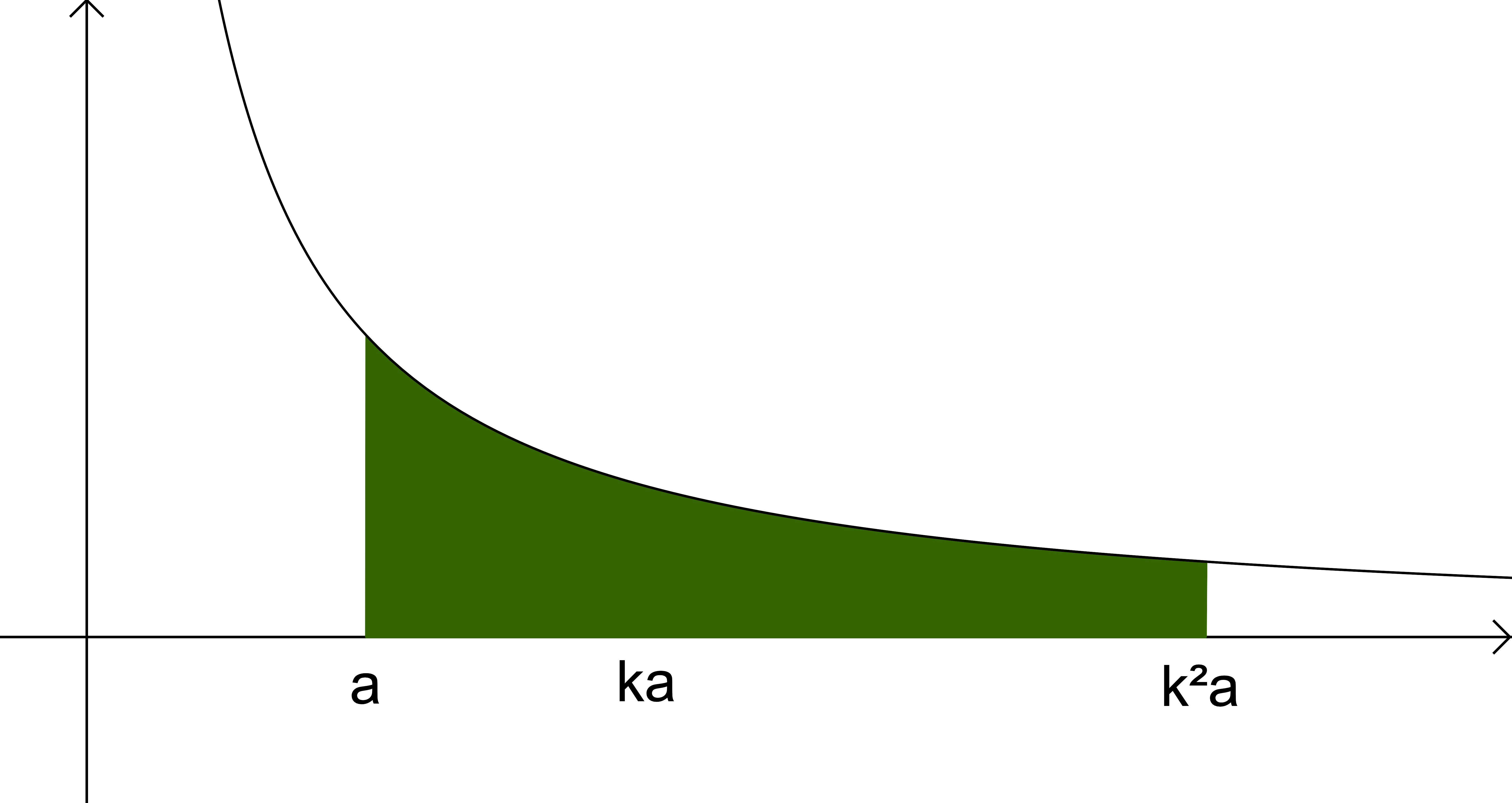
当直角双曲线下的两段面积相等时，x的值呈等比数列，x2/x1=x1/x0=k，y的值也呈等比数列，y2/y1=y1/y0=1/k。

约翰·纳皮尔在1614年以及Jost Bürgi在6年后，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数，当时还没出现有理数幂的概念，直到1742年William Jones才发表了现在的幂指数概念。按后世的观点，Jost Bürgi的底数1.0001相当接近自然对数的底数e，而约翰·纳皮尔的底数0.9999999相当接近1/e。实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，Henry Briggs（英语：Henry Briggs (mathematician)）建议纳皮尔改用10为底数未果，他用自己的方法于1624年部分完成了常用对数表的编制。

形如f(x) = x的曲线都有一个代数反导数，除了特殊情况p = −1对应于双曲线的弓形面积（英语：Quadrature (mathematics)），即双曲线扇形；其他情况都由1635年发表的卡瓦列里弓形面积公式（英语：Cavalieri"s quadrature formula）给出，其中抛物线的弓形面积由公元前3世纪的阿基米德完成（抛物线的弓形面积（英语：The Quadrature of the Parabola）），双曲线的弓形面积需要发明一个新函数。1647年Grégoire de Saint-Vincent（英语：Grégoire de Saint-Vincent）将对数联系于双曲线xy=1的弓形面积，他发现x轴上[a,b]两点对应的双曲线线段与原点围成的双曲线扇形同[c,d]对应的扇形，在a/b=c/d时面积相同，这指出了双曲线从x = 1到x = t的积分f(t)满足：

1649年，Alphonse Antonio de Sarasa（英语：Alphonse Antonio de Sarasa）将双曲线下的面积解释为对数。大约1665年，伊萨克·牛顿推广了二项式定理，他将1/(1+x)展开并逐项积分，得到了自然对数的无穷级数。“自然对数”最早描述见于尼古拉斯·麦卡托在1668年出版的著作《Logarithmotechnia》中，他也独立发现了同样的级数，即自然对数的麦卡托级数。大约1730年，欧拉定义互为逆函数的指数函数和自然对数为：

形式定义

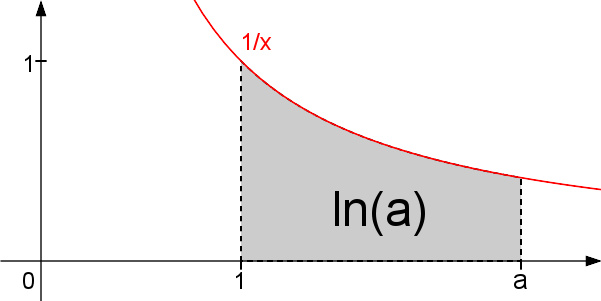
ln(a)展现为曲线 f(x) = 1/x从1至a下的面积。如果a小于1，从a到1的面积计为负数。

欧拉定义自然对数为序列的极限：

ln(a)正式定义为积分，

这个函数为对数是因满足对数的基本性质:

这可以通过将定义了ln(ab)的积分拆分为两部分，并在第二部分中进行换元x = ta来证实:

幂公式ln(t) = r ln(t)可如下推出:

第二个等式使用了换元u = x。

自然对数还有在某些情况下更有用的另一个积分表示：

性质

ln⁡ ⁡ -->(1)=∫ ∫ -->111tdt=0{\displaystyle \ln(1)=\int _{1}^{1}{\frac {1}{t}}\,dt=0\,}

ln⁡ ⁡ -->(− − -->1)=iπ π -->{\displaystyle \ln(-1)=i\pi \,}

ln⁡ ⁡ -->(x)(y)for0<x<y{\displaystyle \ln(x)

limx→ → -->0ln⁡ ⁡ -->(1+x)x=1{\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1\,}

ln⁡ ⁡ -->(xy)=yln⁡ ⁡ -->(x){\displaystyle \ln(x^{y})=y\,\ln(x)\,}

x− − -->1x≤ ≤ -->ln⁡ ⁡ -->(x)≤ ≤ -->x− − -->1forx>0{\displaystyle {\frac {x-1}{x}}\leq \ln(x)\leq x-1\quad {\rm {for}}\quad x>0\,}

ln⁡ ⁡ -->(1+xα α -->)≤ ≤ -->α α -->xforx≥ ≥ -->0,α α -->≥ ≥ -->1{\displaystyle \ln {(1+x^{\alpha })}\leq \alpha x\quad {\rm {for}}\quad x\geq 0,\alpha \geq 1\,}

导数

自然对数的图像和它在x = 1.5处的切线。

ln(1 + x)的泰勒多项式只在−1 x ≤ 1范围内有逐步精确的近似。

自然对数的导数为

证明一 （微积分第一基本定理）:ddxln⁡ ⁡ -->(x)=ddx∫ ∫ -->1x1tdt=1x{\displaystyle {\frac {d}{dx}}\ln(x)={\frac {d}{dx}}\int _{1}^{x}{\frac {1}{t}}\,dt={\frac {1}{x}}}

证明二:按此影片

设 u=hx⇒ ⇒ -->ux=h{\displaystyle u={\frac {h}{x}}\Rightarrow ux=h}

设 n=1u⇒ ⇒ -->u=1n{\displaystyle n={\frac {1}{u}}\Rightarrow u={\frac {1}{n}}}

用自然对数定义的更一般的对数函数，logb(x) = ln(x)/ln(b)，根据其逆函数即一般指数函数的性质，它的导数为：

根据链式法则，以f(x)为参数的自然对数的导数为

右手端的商叫做f的对数导数（英语：logarithmic derivative），通过ln(f(x))的导数的方法计算f"(x)叫做对数微分。

幂级数

自然对数的导数性质导致了ln(1 + x)在0处的泰勒级数，也叫做麦卡托级数：

把x − 1代入x中，可得到ln(x)自身的级数。通过在麦卡托级数上使用欧拉变换，可以得到对绝对值大于1的任何x有效的如下级数:

这个级数类似于贝利-波尔温-普劳夫公式。

还要注意到xx− − -->1{\displaystyle x \over {x-1}}是自身的逆函数，所以要生成特定数y的自然对数，简单把xx− − -->1{\displaystyle x \over {x-1}}代入x中。

自然数的倒数的总和

叫做调和级数。它与自然对数有密切联系：当n趋于无穷的时候，差

收敛于欧拉-马歇罗尼常数。这个关系有助于分析算法比如快速排序的性能。

积分

自然对数通过分部积分法积分:

假设:

所以:

自然对数可以简化形如g(x) = f "(x)/f(x)的函数的积分：g(x)的一个原函数给出为ln(|f(x)|)。这是基于链式法则和如下事实:

换句话说，

且

例子

下面是 g(x) = tan(x)的例子:

设 f(x) = cos(x) 且 f"(x)= – sin(x):

与双曲函数的关系

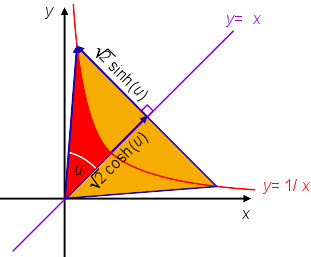
在直角双曲线(方程y = 1/x)下，双曲线三角形(黄色)，和对应于双曲角u的双曲线扇形(红色)。这个三角形的边分别是双曲函数中cosh和sinh的√2倍。

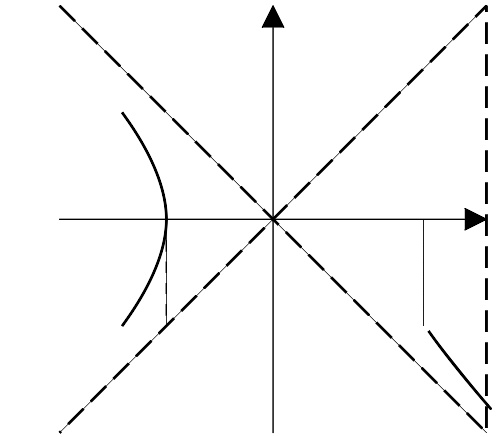
射线出原点交单位双曲线x2 − − --> y2 = 1{\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}于点(cosha,sinha){\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}，这里的a{\displaystyle \scriptstyle a}是射线、双曲线和x{\displaystyle \scriptstyle x}轴围成的面积的二倍。对于双曲线上位于x轴下方的点，这个面积被认为是负值。

在18世纪，约翰·海因里希·兰伯特介入了双曲函数，并计算了双曲几何中双曲三角形的面积。对数函数是在直角双曲线xy=1{\displaystyle xy=1}下定义的，可构造双曲线直角三角形，底边在线y=x{\displaystyle y=x}上，一个顶点是原点，另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数，是自然对数的逆函数指数函数，即要形成指定双曲角u，在渐进线即x或y轴上需要有的x或y的值。显见这里的底边是(eu+e− − -->u)22{\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}，垂线是(eu− − -->e− − -->u)22{\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}。

通过旋转和缩小线性变换，得到单位双曲线下的情况，有：

cosh⁡ ⁡ -->x=ex+e− − -->x2{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}

sinh⁡ ⁡ -->x=ex− − -->e− − -->x2{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}

单位双曲线中双曲线扇形的面积是对应直角双曲线xy=1{\displaystyle xy=1}下双曲角的 1/2。

连分数

尽管自然对数没有简单的连分数，但有一些广义连分数如:

这些连分数特别是最后一个对接近1的值快速收敛。但是，更大的数的自然对数，可以轻易的用这些更小的数的自然对数的加法来计算，带有类似的快速收敛。

例如，因为2 = 1.25 × 1.024，2的自然对数可以计算为:

进而，因为10 = 1.25 × 1.024，10的自然对数可以计算为:

复数对数

指数函数可以扩展为对任何复数x得出复数值为e的函数，只需要简单使用x为复数的无穷级数；这个指数函数的逆函数形成复数对数，并带有正常的对数的多数性质。但是它涉及到了两个困难: 不存在x使得e = 0；并且有着e = 1 = e。因为乘法性质仍适用于复数指数函数，e = e，对于所有复数z和整数n。

所以对数不能定义在整个复平面上，并且它是多值函数，就是说任何复数对数都可以增加2πi的任何整数倍而成为等价的对数。复数对数只能在切割平面上是单值函数。例如，ln i = 1/2 πi 或 5/2 πi 或 −3/2 πi 等等；尽管 i = 1，4 log i 不能定义为 2πi 或 10πi 或 −6 πi，以此类推。

自然对数函数在复平面（主分支）上的绘图

z = Re(ln(x+iy))

前三图的叠加

主值定义

对于每个非0复数z = x + yi，主值Log z是虚部位于区间(−π,π]内的对数。表达式Log 0不做定义，因为没有复数w满足e = 0。

要对Log z给出一个公式，可以先将z表达为极坐标形式，z = re。给定z，极坐标形式不是确切唯一的，因为有可能向θ增加2π的整数倍，所以为了保证唯一性而要求θ位于区间(−π,π]内；这个θ叫做幅角的主值，有时写为Arg z或atan2(y,x)。则对数的主值可以定义为 ：

例如，Log(-3i) = ln 3 − πi/2。

常见科学用法

自然指数有应用于表达放射衰变（放射性）之类关于衰减的过程，如放射性原子数目N随时间变化率dN/dt=-pN，常数p为原子衰变概率，积分得N(t)=N(0)·exp(-pt)。

参考

John B. Conway, Functions of one complex variable, 2nd edition, Springer, 1978.

Serge Lang, Complex analysis, 3rd edition, Springer-Verlag, 1993.

Gino Moretti, Functions of a Complex Variable, Prentice-Hall, Inc., 1964.

Donald Sarason, Complex function theory, 2nd edition, American Mathematical Society, 2007.

E. T. Whittaker and G. N. Watson, A Course in Modern Analysis, fourth edition, Cambridge University Press, 1927.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。