弗莱纳公式

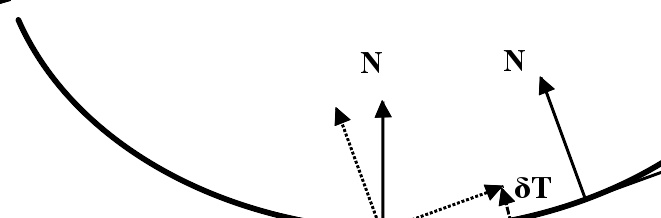
平面曲线上的亮点的切向量和法向量，以及标架在运动过程中的旋转。

记 r (t) 为欧式空间 R 中的曲线，表示粒子在时间 t 时刻的位置向量。 弗莱纳公式只适用于正则曲线，即速度向量 r ′(t)和加速度向量 r ′′(t)不为零的曲线。

记 s(t) 为 t 时刻粒子所在位置到曲线上某定点的弧长：

由于假设 r ′ ≠ 0，因此可以将 t 表示为 s 的函数，因此可将曲线表示为弧长 s 的函数 r (s) = r ( t ( s ))。 s 通常也被称为曲线的弧长参数。

对于由弧长参数定义的正则曲线 r ( s )， 弗莱纳标架 (或 弗莱纳基底 )定义如下：

单位切向量 T ：

主法向量 N ：

副法向量 B 定义为 T 和 N 的外积：

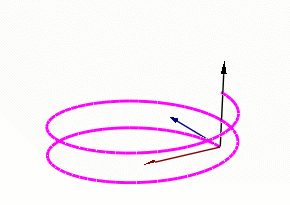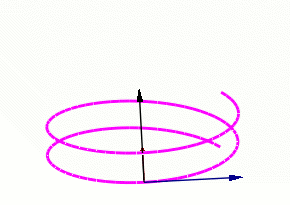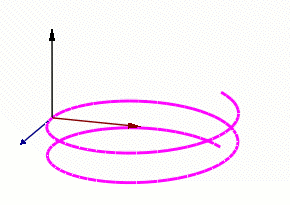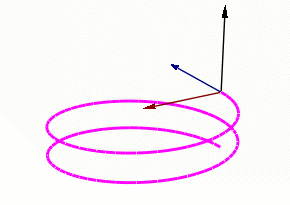
螺旋线上弗莱纳标架的运动。蓝色的箭头表示切向量，红色的箭头表示法向量，黑色的箭头表示副法向量。

由于 | T | = 1 , d ( T ⋅ ⋅ --> T ) d s = 2 T ⋅ ⋅ --> N = 0 , {\displaystyle |\mathbf {T} |=1,{\frac {d(\mathbf {T} \cdot \mathbf {T} )}{ds}}=2\mathbf {T} \cdot \mathbf {N} =0,} 所以 N 与 T 垂直。 方程 (3) 说明 B 垂直于 T 和 N ，因此向量 T ， N ， B 互相垂直。

弗莱纳公式如下：

其中 κ 为曲线的曲率，τ 为曲线的挠率。

弗莱纳公式有时也被称作 弗莱纳定理 ，并且可以写做矩阵的形式：

其中的矩阵是反对称矩阵。

对弧长s求导，可以看成是对切方向的协变导数。

参阅

曲线仿射几何

曲线微分几何

达布标架

运动学

参考资料

Crenshaw, H.C.; Edelstein-Keshet, L., Orientation by Helical Motion II. Changing the direction of the axis of motion, Bulletin of Mathematical Biology, 1993, 55 (1): 213–230

Etgen, Garret; Hille, Einar; Salas, Saturnino, Salas and Hille"s Calculus — One and Several Variables 7th, John Wiley & Sons: 896, 1995

Frenet, F.,Sur les courbes à double courbure (PDF) , Thèse, Toulouse, 1847 . Abstract in J. de Math. "17" , 1852.

Goriely, A.; Robertson-Tessi, M.; Tabor, M.; Vandiver, R., Elastic growth models,BIOMAT-2006 (PDF) , Springer-Verlag, 2006 .

Griffiths, Phillip, On Cartan"s method of Lie groups and moving frames as applied to uniqueness and existence questions in differential geometry, Duke Mathematics Journal, 1974, 41 (4): 775–814, doi:10.1215/S0012-7094-74-04180-5 .

Guggenheimer, Heinrich, Differential Geometry, Dover, 1977, ISBN 0-486-63433-7

Hanson, A.J.,Quaternion Frenet Frames: Making Optimal Tubes and Ribbons from Curves (PDF) , Indiana University Technical Report, 2007

Iyer, B.R.; Vishveshwara, C.V., Frenet-Serret description of gyroscopic precession, Phys. Rev., D, 1993, 48 (12): 5706–5720

Jordan, Camille, Sur la théorie des courbes dans l"espace à n dimensions, C. R. Acad. Sci. Paris, 1874, 79 : 795–797

Kühnel, Wolfgang, Differential geometry, Student Mathematical Library 16 , Providence, R.I.: American Mathematical Society, 2002, ISBN 978-0-8218-2656-0,MR1882174

Serret, J. A.,Sur quelques formules relatives à la théorie des courbes à double courbure (PDF) , J. De Math., 1851, 16 .

Spivak, Michael, A Comprehensive Introduction to Differential Geometry (Volume Two), Publish or Perish, Inc., 1999 .

Sternberg, Shlomo, Lectures on Differential Geometry, Prentice-Hall, 1964

Struik, Dirk J., Lectures on Classical Differential Geometry, Reading, Mass: Addison-Wesley, 1961 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。