圆堆砌

正六边形镶嵌可以被用来进行 圆堆砌 （ 英语 ： Circle packing ） ，以其每个顶点为圆心放置等直径的圆。在这个堆砌里，每个圆都与3个相邻圆接触（ 接触数 （ 英语 ： Kissing number problem ） ）。每个正六边形中间的部分实际上还可以再放入一个圆，这样我们就会得到二维最密圆堆砌——正三角形镶嵌式圆堆砌，这时接触数达到最大值6。

半正涂色

正六边形镶嵌共有3种不同的 半正涂色 （ 英语 ： Uniform coloring ） ，都可以由 Wythoff （ 英语 ： Wythoff constructions ） 镜面对称构造出来。(h,k)表示一种涂色的面周期性重复，以正六边形距离h、k计数，h在先，k在后。

其中三色正六边形镶嵌是一个由三阶 全序多胞形 （ 英语 ： permutohedron ） 产生的镶嵌。

相关半正镶嵌

正六边形镶嵌可以通过截角操作得到一系列与之相关的半正镶嵌，其与正六边形镶嵌拥有相似的对称性：

正六边形镶嵌在拓扑上与一系列一直延伸到双曲镶嵌的顶点图为 n 的（广义）多面体相关：

（三阶）正六边形镶嵌在拓扑上与一系列面为正六边形的密铺相关联，这些镶嵌都可称之为“正六边形镶嵌”，所以我们以“n 阶”来区分，其施莱夫利符号为{6,n}， 考克斯特符号 （ 英语 ： Coxeter diagram ） ，一直到n = ∞：

这个镶嵌还是一系列有考克斯特对称群[n,3]对称性的（半）截角菱形多面体或镶嵌的一员。立方体可以被看作是“菱形六面体”，这里菱形就是正方形。它们的截角形在原顶点处有正的多边形，而原来的菱形面则被截成了非正六边形。这一系列多面体或镶嵌有两种顶点图：(n.6.6)和(6,6,6)。

正六边形镶嵌亦可被看作 延长菱形镶嵌 ，菱形镶嵌的每一个顶点都被延长成了新的棱。这类似于三维空间中的菱形十二面体堆砌和菱形六角化十二面体堆砌之间的关系。

基于正六边形镶嵌和正三角形镶嵌的Wythoff构建

就像半正多面体一样，这里也有8个基于正六边形镶嵌（和正三角形镶嵌）的半正镶嵌。在以下的图片中，原有面对应的面被涂成了红色，原有顶点所对应的面被涂成了黄色，原有棱对应的面被涂成了蓝色。这8个半正镶嵌中，只有7个是拓扑上相异的。（截顶正三角形镶嵌与正六边形镶嵌在拓扑上相同）

拓扑相同的镶嵌

正六边形镶嵌是有着{6,3}拓扑的一种特殊的正的镶嵌，而实际上，这里有12种类型的非正但是 面全同 （ 英语 ： face-transitivity ） 且 顶点全同 （ 英语 ： vertex-transitivity ） 的六边形镶嵌，前7种可以被认为是没有边对边正好对上的四边形镶嵌，也可被认为是有两对共线边的六边形镶嵌。这里的“对称性”假定所有的面都是相同的。

平行四边形 p2对称

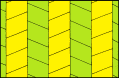
平行四边形 pmg对称

平行四边形 pgg对称

矩形 pgg对称

梯形 pmg对称

矩形 pgg对称

矩形 cmm对称

六边形 p2对称

六边形 pgg对称

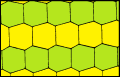
六边形 pmg对称

展长六边形 cmm对称

正六边形 p6m对称

正六边形镶嵌也可被变形为一种手征性的四填充色三向同性的编织图案。其中部分正六边形被扭曲成了平行四边形。这一图案有着旋转 632 (p6) 对称性 （ 英语 ： List_of_planar_symmetry_groups#Wallpaper_groups ） 。

应用

正六边形镶嵌是二维空间最密的排列方式。在蜂窝猜想中，正六边形镶嵌是使用最少的总周长将该表面划分成面积相等的区域的最佳方法。 最佳的三维结构由开尔文勋爵(Lord Kelvin)提出，他认为， 开尔文结构 （ 英语 ： Kelvin structure ） (体心立方晶格)是最佳的结构（最佳结构可能出现于肥皂泡）。然而，一个更加不对称的 威尔-费兰结构 （ 英语 ： Weaire–Phelan structure ） 要比它好一些。

参考文献

Coxeter, H.S.M. Regular Polytopes , (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs

Grünbaum, Branko ; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings , p. 58-65)

MathWorld上 Hexagonal Grid 的资料，作者：埃里克·韦斯坦因。

Richard Klitzing, 2D Euclidean tilings,o3o6x - hexat - O3

Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979: 35. ISBN 0-486-23729-X.

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5[1]

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。