历史

早在14世纪，尼克尔·奥里斯姆已经证明调和级数发散，但知道的人不多。17世纪时，皮耶特罗·曼戈里（英语：Pietro Mengoli）、约翰·伯努利和雅各布·伯努利完成了全部证明工作。

调和序列历来很受建筑师重视；这一点在巴洛克时期尤其明显。当时建筑师在建造教堂和宫殿时，运用调和序列为楼面布置和建筑物高度建立比例，并使室内外的建筑细节间呈现和谐的联系。

佯谬

只要有足够多的骨牌，最顶层骨牌离最底层的距离就可以无穷远。可以发现，图中骨牌排列的形状就像顺时针旋转90°的对数函数，也即函数y=1/x的不定积分。

对刚接触这个级数的人而言，调和级数是违反直觉的——尽管随着n不断增大，1/n无限接近0，但它却是一个发散级数。调和级数也因此成为一些佯谬的原型。“橡皮筋上的蠕虫”就是其中一个例子。假设一条蠕虫沿着一条1米长的橡皮筋爬行，而橡皮筋每分钟匀速伸展1米。如果相对于其所在的橡皮筋，蠕虫的爬行速度是每分钟1厘米，那么它最终会到达橡皮筋的另一头吗？与直觉相反，答案是肯定的：n分钟之后，蠕虫爬行过的距离与橡皮筋总长度的比值为：

由于调和级数发散（证明见本条目“发散性”一节），即n趋于无穷大时级数也趋于无穷大，所以这个比值也必定在某个时刻超过1；也就是说，蠕虫最终一定会到达橡皮筋另一头。然而，在这个时刻的n的值极其之大，约为e，超过10（1后面有40个零）。这也说明了，尽管调和级数确确实实是发散的，但它发散的速度非常慢。

另一个例子：假设你有一堆完全相同的骨牌，可以肯定的是，你可以把它们叠在一起，并使得每个骨牌都突出其下方骨牌外一定长度，最终使得最上层的骨牌完全在最底层骨牌以外甚至更远。违反直觉的是，只要你的骨牌足够多，你就可以使最上层的骨牌可以离最底层骨牌无穷远。一个较简单的证明如下：

设每一块骨牌的长度为l0{\displaystyle l_{0}}。再设一叠n个平衡的骨牌的质心与最底层骨牌最右端的距离为dn{\displaystyle d_{n}}；在只有1个骨牌时，质心就在骨牌的几何中心（假设骨牌密度均匀），即d1=l02{\displaystyle d_{1}\,=\,{\frac {l_{0}}{2}}}。对于一叠刚好平衡的骨牌（即对于任意一层骨牌，在其之上的骨牌的质心恰好落在其边缘），新骨牌不置于其上方（否则使得质心往右偏移而倒塌），而是垫在整叠骨牌之下，并使得原有骨牌的质心刚好落在新骨牌的最左端（则原来的骨牌不会倒塌）；设从上往下第n层骨牌突出其下方骨牌的长度为ln{\displaystyle l_{n}}，则有：dn+ln=l0{\displaystyle d_{n}+l_{n}=l_{0}}。根据质心的坐标系计算公式，可得到新的骨牌叠的质心为：

则ln+1=l0− − -->dn+1=l02n+1{\displaystyle l_{n+1}=l_{0}-d_{n+1}={\frac {\frac {l_{0}}{2}}{n+1}}}，即ln=l02⋅ ⋅ -->1n{\displaystyle l_{n}={\frac {l_{0}}{2}}\cdot {\frac {1}{n}}}。

也就是说，理想的摆法是：最顶层骨牌与第二层之间水平距离是骨牌长度的1/2，第二、三层间水平距离是骨牌长度的1/4，第三、四层之间水平距离是骨牌长度的1/6……依此类推。最终，最顶层和最底层骨牌的水平距离是：

因为调和级数发散，所以当骨牌数目n趋于无穷大时，水平距离也趋于无穷大。

发散性

比较审敛法

因此该级数发散。

积分判别法

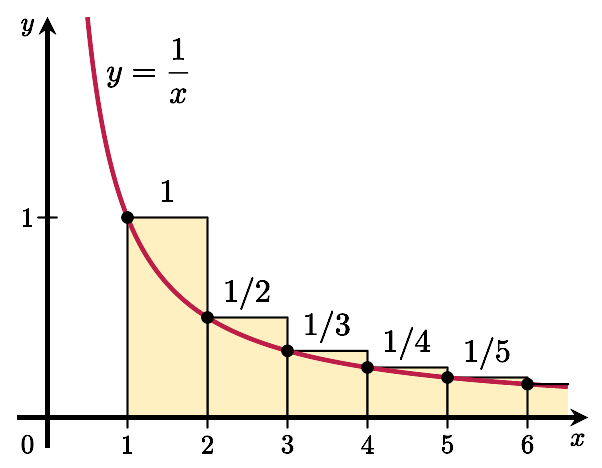
通过将调和级数的和与一个瑕积分作比较可证此级数发散。考虑右图中长方形的排列。每个长方形宽1个单位、高1 / n个单位（换句话说，每个长方形的面积都是1 / n），所以所有长方形的总面积就是调和级数的和： 矩形面积和:=1+12+13+14+15+⋯ ⋯ -->.{\displaystyle =1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots .} 而曲线y = 1 / x以下、从1到正无穷部分的面积由以下瑕积分给出： 曲线下面积:=∫ ∫ -->1∞ ∞ -->1xdx=∞ ∞ -->.{\displaystyle =\int _{1}^{\infty }{\frac {1}{x}}\,dx\;=\;\infty .} 由于这一部分面积真包含于（换言之，小于）长方形总面积，长方形的总面积也必定趋于无穷。更准确地说，这证明了：

这个方法的拓展即积分判别法。

反证法

假设调和级数收敛 , 则：

limn→ → -->∞ ∞ -->S2n− − -->Sn=0{\displaystyle \lim _{n\to \infty }S_{2n}-S_{n}=0}

但与 S2n− − -->Sn=1n+1+1n+2+1n+3+⋯ ⋯ -->+12n>n2n=12{\displaystyle S_{2n}-S_{n}={\frac {1}{n+1}}+{\frac {1}{n+2}}+{\frac {1}{n+3}}+\cdots +{\frac {1}{2n}}>{\frac {n}{2n}}={\frac {1}{2}}} 矛盾，故假设不真，即调和级数发散。

发散率

调和级数发散的速度非常缓慢。举例来说，调和序列前10项的和还不足100。这是因为调和数列的部分和呈对数增长。特别地，

其中γ γ -->{\displaystyle \gamma欧拉是欧拉-马歇罗尼常数，而ϵ ϵ -->k{\displaystyle \epsilon _{k}}约等于12k{\displaystyle {\frac {1}{2k}}}，并且随着 k{\displaystyle k} 趋于正无穷而趋于0{\displaystyle 0}。这个结果由欧拉给出。

部分和

调和级数的第n个部分和为：

也叫作第n个调和数。

第n个调和数与n的自然对数的差值（即∑ ∑ -->k=1n1k− − -->ln⁡ ⁡ -->n{\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln n}）收敛于欧拉-马歇罗尼常数。

两个不同的调和数之间的差值永远不是整数。

除了n=1时以外，没有任何一个调和数是整数。

相关级数

交错调和级数

此图显示，交错调和级数的前14个部分和（图中黑色线段）收敛于2的自然对数（红色直线）。

如下级数：

被称作交错调和级数。这个级数可经交错级数判别法证明收敛。特别地，这个级数的和等于2的自然对数：

这个公式是墨卡托级数（自然对数的泰勒级数形式）的一个特例。

从反正切函数的泰勒展开式可以导出一个相关级数：

这个级数也被称作π的莱布尼茨公式。

广义调和级数

广义调和级数是指有如下形式的级数：

其中 a≠ ≠ -->0{\displaystyle a\neq 0} 且 b{\displaystyle b} 为实数。

由比较审敛法可证所有广义调和级数均发散。

P-级数

调和级数广义化的其中一个结果是p-级数，定义如下：

其中P是任意正实数。当p=1，p级数即调和级数。由积分判别法或柯西并项判别法（en:Cauchy condensation test（英文））可知p-级数在p>1时收敛（此时级数又叫过调和级数（over-harmonic series）），而在p ≤ 1时发散。 当p>1时，p-级数的和即ζ(p)，也就是黎曼ζ函数在p的值。

φ-级数

对一个凸实值函数φ，若满足以下条件：

则级数∑n≥1 φ(n)收敛。

随机调和级数

随机调和级数定义如下：

其中sn是独立的、恒等分布的随机变量，取值范围为+1和-1，取这两个值的概率都是1/2。阿尔伯塔大学的拜伦·施姆兰研究此级数的性质，并发现这个级数收敛的概率为1，并发现这个随机变量有着一些有趣的性质。特别地，这个随机变量的概率密度函数在+2和-2处的值为0.124999999999999999999999999999999999999999764…，与1/8只差了不到10。施姆兰的论文解释了为什么这个概率如此接近、但却不是1/8。这个概率的精确值是由无穷余弦乘积积分C2{\displaystyle C_{2}}除以π而给出的。

贫化调和级数

贫化调和级数是将调和级数中、分母含有数字9的项去除后所剩的级数。这个级数是收敛的，和小于80。实际上，将包含任意数字串的项从调和级数中去除后，所剩级数都收敛。

拉玛努金和

调和级数是柯西发散的，而且很多常用的发散级数求和方法（如博雷尔求和法）对它也不适用。但是，调和级数的拉玛努金和存在，且为欧拉-马歇罗尼常数。

参见

无穷级数

调和平均数

黎曼ζ函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。