导体与电阻器

  一个750-kΩ的电阻器，其外表色码标识出它的电阻值。电阻表可以用来验证它的电阻值。

像电线一类的物体，具有低电阻，可以很有效率地传输电流，这类物体称为“导体”。通常导体是由像铜、金和银一类具有优等导电性质的金属制造，或者次等导电性质的铝。电阻器是具有特定电阻的电路元件。制备电阻器所使用的原料有很多种；应该使用哪种原料，要视指定的电阻、能量耗散、准确度和成本等因素而定。

直流电

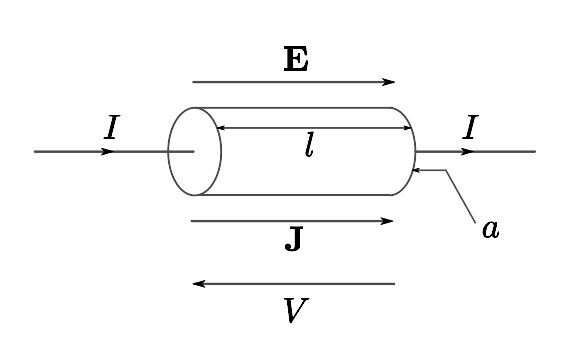
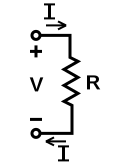
  处于均匀外电场的均匀截面导体（例如，电线）。

在物理学里，对于物质的微观层次电性质研究，会使用到的欧姆定律，以矢量方程表达为

其中， E {\displaystyle \mathbf {E} } 是电场， ρ ρ --> {\displaystyle \rho } 是电阻率， J {\displaystyle \mathbf {J} } 是电流密度。

在导体内任意两点g、h，定义电压为将单位电荷从点g移动到点h，电场力所需做的机械功 ：

其中， V g h {\displaystyle V_{gh}} 是电压， w {\displaystyle w} 是机械功， q {\displaystyle q} 是电荷量， d l {\displaystyle \mathrm {d} \mathbf {l} } 是微小线元素。

假设，沿着积分路径，电流密度 J = J l ^ ^ --> {\displaystyle \mathbf {J} =J{\hat {\mathbf {l} }}} 为均匀电流密度，并且平行于微小线元素：

其中， l ^ ^ --> {\displaystyle {\hat {\mathbf {l} }}} 是积分路径的单位矢量。

那么，可以得到电压：

其中， l {\displaystyle l} 是积分路径的径长。

假设导体具有均匀的电阻率，则通过导体的电流密度也是均匀的：

其中， a {\displaystyle a} 是导体的截面面积。

电压 V g h {\displaystyle V_{gh}} 简写为 V {\displaystyle V} 。电压与电流成正比：

总结，电阻与电阻率的关系为

假设 J > 0 {\displaystyle J>0} ，则 V > 0 {\displaystyle V>0} ；将单位电荷从点g移动到点h，电场力需要作的机械功 w > 0 {\displaystyle w>0} 。所以，点g的电势比点h的电势高，从点g到点h的电势差为 − − --> V {\displaystyle -V} 。从点g到点h，电压降是 V {\displaystyle V} ；从点h到点g，电压升是 V {\displaystyle V} 。

交流电

假设电线传导的电流是高频率交流电，则由于趋肤效应，电线的有效截面面积会减小。假设平行排列几条电线在一起，则由于邻近效应，每一条电线的有效电阻会大于单独电线的电阻。对于普通家用交流电，由于频率很低，这些效应非常微小，可以忽略这些效应。

测量电阻

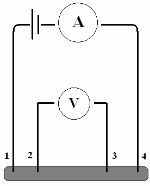
  四端点量测技术可以用来准确地测量点2与点3之间的电阻。

电阻计是测量电阻的仪器。由于探针电阻和接触电阻会造成电压降，简单电阻器不能准确地测量低电阻。高准确度测量工作必须使用四端点测量技术（ four-terminal measurement technology ）。

能带理论概述

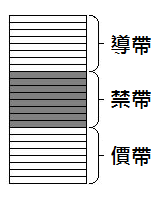
  绝缘体的电子能级。

根据量子力学，束缚于原子内部的电子，其能量不能假定为任意数值，而只能占有某些固定能级，在这些能级之间的数值不可能是电子的能量。这些能级可以分为两组，一组称为导带，另一组称价带。导带的能级通常比较高一些。处于导带的电子可以自由地移动于物体内部。

在绝缘体和半导体中，原子之间会相互影响，使得导带和价带之间出现禁带，电子无法处于禁带。为了要产生电流，必须给予电子相当大的能量，协助电子从价带，跳过禁带，进入导带。因此，即使对这些物质施加很大的电压，产生的电流仍旧很小。

电阻种类

碳膜电阻

金属氧化膜电阻

精密电阻

绕线电阻

水泥电阻

固定瓷管电阻

低感瓷管电阻

铝壳精密电阻

光敏电阻

热敏电阻

压敏电阻

各种不同材料的电阻

金属

金属是一群原子以晶格结构形成的晶体，每个原子都拥有一层（或多层）由电子组成的外壳。处于外壳的电子能脱离原子核的吸引力而到处流动，形成一片电子海，使得金属能够导电。当施加电势差（即电压）于金属两端时，因为感受到电场的影响，这些自由电子会呈加速运动。但是每当自由电子与晶格发生碰撞，其动能会遭受损失，以热能的形式将能量释放，所以，电子的平均移动速度是漂移速度，其方向与电场方向相反。由于漂移运动，会产生电流。在现实中，物质的原子排列不可能为完全规则，因此电子在流动途中会被不按规则排列的原子散射，这是电阻的来源。

给予一个具有完美晶格的金属晶体，移动于这晶体的电子，其运动等价于移动于自由空间、具有有效质量的电子的运动。所以，假设热运动足够微小，周期性结构没有偏差，则这晶体的电阻等于零。但是，真实晶体并不完美，时常会出现晶体缺陷，有些晶格点的原子可能不存在，可能会被杂质侵占。这样，晶格的周期性会被扰动，因而电子会被散射。另外，假设温度大于绝对零度，则处于晶格点的原子会发生热震动，因而出现热震动的粒子——声子——移动于晶体。温度越高，声子越多。声子会与电子发生碰撞，这过程称为晶格散射（ lattice scattering ）。主要由于上述两种散射，自由电子的流动会被阻碍，晶体因此具有有限电阻 。

半导体和绝缘体

对于金属，费米能级的位置在导带区域内，因此金属内部会出现自由的传导电子。可是，对于半导体，费米能级的位置在能隙区域内。

本征半导体是未被掺杂的半导体，其费米能级大约为导带最低值与价带最高值的平均值。当温度为绝对零度时，本征半导体内部没有自由的传导电子，电阻为无穷大。当温度开始上升，高于绝对零度时，有些电子可能会获得能量而进入传导带中；假设施加外电场，则这些电子在获得外电场的能量后，会移动于金属内部，因而形成电流。

杂质半导体是经过掺杂的半导体。靠着捐赠电子给导带，或价带接受空穴，外质半导体内部的杂质原子能够增加电荷载子的密度，从而减低电阻。高度渗杂的半导体的导电性质类似金属。在非常高温度状况，热生成电荷载子的贡献会超过杂质原子的贡献；随着温度的增加，电阻会呈指数递减。

离子液体／电解质

在电解质中，电流是由带电的离子的流动产生，因此液体的电阻很受盐的浓度所影响。譬如蒸馏水是绝缘体，但盐水就是很好的导电体。

在生物体内的细胞膜，离子盐负责电流的传送。细胞膜中的小孔道，称为离子通道，会选择什么离子可以通过。这直接决定了细胞膜的电阻。

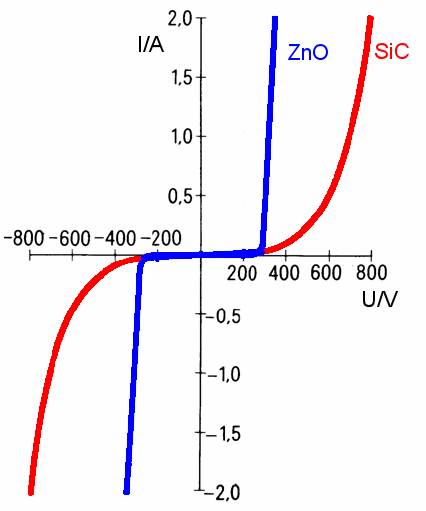
非欧姆元件

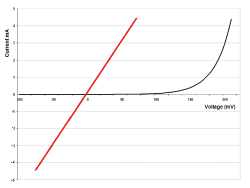
  电流对电压线图。理想电阻器和PN接面二极管的I-V线分别以红色和黑色显示。

有些电路元件不遵守欧姆定律，它们的电压与电流之间的关系（I-V线）乃非线性关系。PN接面二极管是一个显明范例。如右图所示，随着二极管两端电压的递增，电流并没有线性递增。给定外电压，可以用I-V线来估计电流，而不能用欧姆定律来计算电流，因为电阻会因为电压的不同而改变称这电阻为“直流电阻”。另外，只有当外电压为正值时，电流才会显著地递增；当施加的电压为负值时，电流等于零。对于这类元件，I-V线的斜率 r {\displaystyle {\mathfrak {r}}} ，称为小信号电阻（ small-signal resistance ）、增量电阻（ incremental resistance ）或动态电阻（ dynamic resistance ），定义为

单位也是欧姆，是很重要的电阻量，适用于计算非欧姆元件的电性 。

温度对电阻的影响

温度对不同物质的电阻会有不同的影响。

导电体

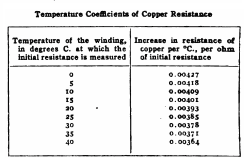
 铜金属在不同温度状况的电阻温度系数 。

假设温度接近室温，则典型金属的电阻 R {\displaystyle R} 通常与温度 T {\displaystyle T} 成正比 ：

其中， R ∗ ∗ --> {\displaystyle R_{*}} 是典型金属在参考温度为 T ∗ ∗ --> {\displaystyle T_{*}} 时的参考电阻， α α --> {\displaystyle \alpha } 是电阻温度系数。

α α --> {\displaystyle \alpha } 是电阻变化百分比每单位温度。每一种物质都有其特定的 α α --> {\displaystyle \alpha } 。实际而言，上述关系式只是近似，真实的物理是非线性的；换句话说， α α --> {\displaystyle \alpha } 本身会随着温度的改变而变化。因此，通常会在 α α --> {\displaystyle \alpha } 字尾添加测量时的温度。例如， α α --> 15 {\displaystyle \alpha _{15}} 是在温度为15 °C时测量的电阻温度系数；使用 α α --> 15 {\displaystyle \alpha _{15}} 为电阻温度系数，则参考温度 T ∗ ∗ --> {\displaystyle T_{*}} 为15 °C，参考电阻为金属在参考温度为15 °C时的参考电阻，而且上述关系式只适用于计算温度在15 °C附近的电阻 R {\displaystyle R} 。

稍加排列，这方程又可表示为

取 R − − --> R ∗ ∗ --> → → --> 0 {\displaystyle R-R_{*}\to 0} 的极限，则可得到微分方程

所以，在温度为 T ∗ ∗ --> {\displaystyle T_{*}} 时，物质的电阻温度系数是，其电阻对温度的曲线在温度为 T ∗ ∗ --> {\displaystyle T_{*}} 时的斜率，除以温度为 T ∗ ∗ --> {\displaystyle T_{*}} 时的电阻。

于1860年代，奥古斯土·马西森想出马西森定则（ Matthiessen"s rule ）。这定则表明，总电阻率 ρ ρ --> {\displaystyle \rho } 可以分为两个项目 ：

其中， ρ ρ --> d {\displaystyle \rho _{d}} 是由于晶体缺陷而产生的电阻率， ρ ρ --> p {\displaystyle \rho _{p}} 是由于声子而产生的电阻率。

ρ ρ --> d {\displaystyle \rho _{d}} 与金属内部的缺陷密度有关，是电阻率对温度的曲线外推至0K时的电阻率。因此， ρ ρ --> d {\displaystyle \rho _{d}} 与温度无关。 ρ ρ --> p {\displaystyle \rho _{p}} 等于 ρ ρ --> − − --> ρ ρ --> d {\displaystyle \rho -\rho _{d}} 。假若缺陷密度不高，则 ρ ρ --> p {\displaystyle \rho _{p}} 通常与缺陷密度无关。 ρ ρ --> p {\displaystyle \rho _{p}} 与电子跟声子的碰撞率有关，而碰撞率与声子密度成正比。假设温度高于德拜温度，则声子密度与温度成正比，所以， ρ ρ --> p {\displaystyle \rho _{p}} 与温度成正比：

其中， C h {\displaystyle C_{h}} 是比例常数。

这方程等价于前面电阻与温度的关系方程。

假设温度低于德拜温度，则电阻与温度的5次方成正比 ：

其中， C l {\displaystyle C_{l}} 是比例常数。

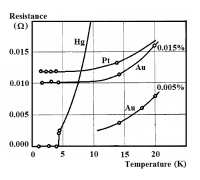
 水银、白金、黄金在不同温度状况的电阻 。

如右图所示，当温度接近绝对温度时，黄金和白金的电阻趋向于常数；而当温度小于4.2K时，水银的电阻突然从0.002欧姆陡降为10 欧姆，成为超导体。

半导体

温度越高，本征半导体的导电性质越优良，电子会被热能撞跳至导带，从而可以自由的移动，也因而留下空穴于价带，也可以自由的移动于价带。这电阻行为以方程表达为

其中， R 0 {\displaystyle R_{0}} ， a {\displaystyle a} 是常数。

外质半导体的电阻对于温度的反应比较复杂。从绝对零度开始，随着温度增加，由于载子迅速地离开施主或受主，电阻会急剧降低。当大多数的施主或受主都失去了载子之后，电阻会因载子的迁移率（ mobility ）下降而随温度稍为上升。当温度升得更高，外质半导体的电阻行为类似本征半导体；施主或受主的载子数量超小于因热能而产生的载子的数量，于是电阻会再度下降 。

绝缘体和电解质

绝缘体和电解质的电阻与温度一般成非线性关系，而且不同物质有不同的变化，故不在此列出概括性的算式。

超导体

主条目：超导体

某些材料在温度接近绝对零度（-273.15°C）时会出现超导现象。

应变对电阻的影响

导体的电阻受应变影响而改变。假设施加张力（一种应力的形式，会引起应变，即导体伸长）于导体，则导体沿张力的方向，其长度会增加，相对而言，导体于垂直张力方向的截面面积会减少。这两种效应共同贡献，使得受到张力的导体，其电阻会随之增加。假设施加压力，则由于压缩（方向相反的应变：导体缩短，截面面积增加），导体应变部分的电阻会减少。应用这效应，应变计（ strain gauge ）可以测量物体的应变与所受张力。

参看

电测量（ electrical measurements ）

热阻（ thermal resistance ）

薄膜电阻

量子霍尔效应，一种新的电阻测量标准。

近藤效应

四端点测量技术

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。