写作背景和年代穆尔和妻子哈莉特·泰勒早在1854年就把这本书的主题列入了他们未来的写作计划。1854-1855年冬天，当穆尔在欧洲旅行时，他开始专注于将这一主题独立成书的想法。基本上可以确定，这本书的初稿主干是在1856-1857年间完成的。穆勒在他的《自传》中提到，他和妻子在此之后多次反复修改润色。穆勒自己说：“我的作品中，没有哪本是像它一样谨慎地写作、细致地修改。”原定一八五八年穆勒从印度事务部退休后，这本书的终稿会确定下来，但那年晚些时候穆勒妻子的死亡让他决定不再继续修改。尽管穆勒通常会于再版中大规模的进行修改，但他认为《论自由》是追忆妻子的“献祭”：“我没有做任何的补充或者修改，我永远也不会。”内容目录严复翻译，上海三联书店出版首篇引论篇二释思想言论自繇篇三释行己自繇明特操为民德之本篇四论国群小己权限之分界篇五论自繇大义之施行康慨翻译，湖南文艺出版社出版第一章引论第二章论思想自由和...

子产敢于理直气壮地跟晋国人论理，是因为他确信一点：只要自己按礼行事，走到哪里都不怕别人挑自己的理。只要自己站得正，就没有什么可以害怕的。对晋国强硬仅仅是一个方面，该尊重的时候一定要尊重，这样才能让晋国人尊重自己。子产和郑简公从晋国回来，紧接着准备派印段前往楚国聘问，这是世界和平协议规定的。去之前，子产专门请子皮派人前往晋国通报此事，以示尊重。随后不久，卫襄公前往楚国朝拜，路过郑国。子产命令印段到城郊招待，随后让外交官子羽陪同卫襄公一行进入国都，游吉和冯简子接待。整个过程符合周礼并且十分周到，卫国人离开的时候非常高兴，称赞郑国“郑有礼，其数世之福也”。舆论导向问题外交无小事。因为一句话，或者因为一餐饭，或者因为一棵树，都有可能引发国际战争，都有可能导致国家的灭亡。所以，外交无小事。子产建立了郑国的外交团队，他们是游吉、子羽、冯简子和裨灶。游吉风度翩翩，对人彬彬有礼，因此人见人爱，走到哪里都受...

内容提要：人格的独立性是孟子“人格自由论”的立论前提，这也是孟子以及有骨气的知识分子与无道的统治者尖锐对立的必然结果。“诚”既是人之所以为人的本体实在，又是人道与天道彼此摩荡的本体基础，因此“诚身”、“明善”都既是形而下的工夫也是宗教性的提升，由此而与天相接，焕发出了人性中美、大、圣、神的创造性。《孟子》的“知言养气章”由以言养勇、以气养勇、以志养勇三个阶梯

1>2>

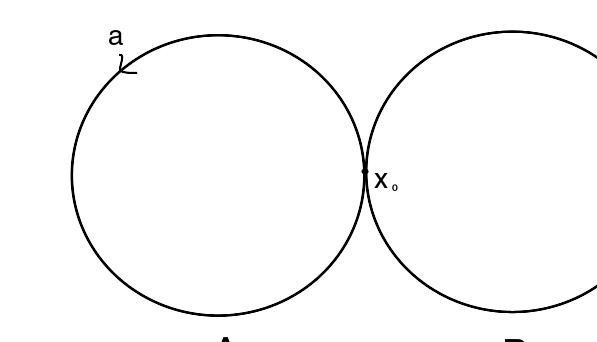
历史在1882年，WaltherDyck在发表于MathematischeAnnalen的论文GruppentheoretischeStudien中研究了自由群的概念，但未加以命名。“自由群”一词由JakobNielsen于1924年引入。例子2个圆环的集丛整数的加法群(Z,+){\displaystyle(\mathbb{Z},+)}是自由群；事实上我们可取S:={1}{\displaystyleS:=\{1\}}。在巴拿赫-塔斯基悖论的论证中用到两个生成元的自由群，以下将予说明。在代数拓扑学中，k{\displaystylek}个圆环的集丛（即：k{\displaystylek}个只交于一点的圆环，见右图）的基本群是k{\displaystylek}个生成元的自由群。建构方式今将构造集合S{\displaystyleS}上之自由群F(S){\displaystyleF(S)}，分解动作...