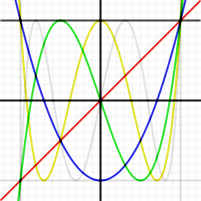
前六个第一类切比雪夫多项式的图像，其中-1¼切比雪夫近似是利用将函数展开为由切比雪夫多项式组成的各项，依需要的逼近程度决定展开的项次，可以得到很接近多项式的结果。此作法类似进行函数的傅立叶分析，只是用切比雪夫多项式代替分析中用到的三角函数。若计算一函数切比雪夫展开的系数：f(x)∼ ∼ -->∑ ∑ -->i=0∞ ∞ -->ciTi(x){\displaystyle f(x)\sim \sum _{i=0}^{\infty }c_{i}T_{i}(x)}

只展开到TN{\displaystyle T_{N}}

项为止，可以得到一个逼近f(x)的N次多项式。对于一个有快速收敛幂级数的函数而言，若展开到一定项次后截止不再展开，截止产生的误差接近截止后的第一项，因此误差可以由截止后的第一项代表。若是用切比雪夫多项式展开，也会有一様的结果。若切比雪夫展开只展开到TN{\displaystyle T_{N}}

，后面截止，其误差会接近TN+1{\displaystyle T_{N+1}}

的整数倍。切比雪夫多项式的特点是在[−1, 1]区间以内．其数值会在+1和−1之间震荡。TN+1{\displaystyle T_{N+1}}

有N+2个极点。因此f(x)和切比雪夫展开的误差接近一个有N+2个极点的函数，因此为近似最佳的N次多项式

。在上面中，可以看到蓝色线（切比雪夫近似的误差）有时比红色线（最佳多项式的误差）接近x轴，但有时蓝色线反而离x轴较远，因此切比雪夫近似和最佳多项式毕竟还是有差异。不过exp函数是快速收敛的函数，切比雪夫近似的误差会比log函数要好。切比雪夫近似是数值积分方法Clenshaw–Curtis正交法（英语：Clenshaw–Curtis quadrature）的基础。雷米兹算法雷米兹算法是在1934年由苏俄数学家雷米兹（英语：Evgeny Yakovlevich Remez）提出的算法

。可用来产生在一定区间内逼近函数f(x)的最佳多项式P(x)。雷米兹算法是一种迭代式的算法，最后会收敛到使误差函数N+2个极值的多项式。雷米兹算法是用以下的事实为基础：可以在有N+2个测试点的情形下，创建一个N次多项式，其误差函数在0附近震荡。假设N+2个测试点x1{\displaystyle x_{1}}

, x2{\displaystyle x_{2}}

, ... xN+2{\displaystyle x_{N+2}}

（其中x1{\displaystyle x_{1}}

和xN+2{\displaystyle x_{N+2}}

假设是区间的二个端点），需求解以下的多项式：P(x1)− − -->f(x1)=+ε ε -->{\displaystyle P(x_{1})-f(x_{1})=+\varepsilon \,}

P(x2)− − -->f(x2)=− − -->ε ε -->{\displaystyle P(x_{2})-f(x_{2})=-\varepsilon \,}

P(x3)− − -->f(x3)=+ε ε -->{\displaystyle P(x_{3})-f(x_{3})=+\varepsilon \,}

⋮ ⋮ -->{\displaystyle \vdots }

P(xN+2)− − -->f(xN+2)=± ± -->ε ε -->.{\displaystyle P(x_{N+2})-f(x_{N+2})=\pm \varepsilon .\,}

等式右侧的正负号交替出现。因此可以得到下式：P0+P1x1+P2x12+P3x13+⋯ ⋯ -->+PNx1N− − -->f(x1)=+ε ε -->{\displaystyle P_{0}+P_{1}x_{1}+P_{2}x_{1}^{2}+P_{3}x_{1}^{3}+\dots +P_{N}x_{1}^{N}-f(x_{1})=+\varepsilon \,}

P0+P1x2+P2x22+P3x23+⋯ ⋯ -->+PNx2N− − -->f(x2)=− − -->ε ε -->{\displaystyle P_{0}+P_{1}x_{2}+P_{2}x_{2}^{2}+P_{3}x_{2}^{3}+\dots +P_{N}x_{2}^{N}-f(x_{2})=-\varepsilon \,}

⋮ ⋮ -->{\displaystyle \vdots }

既然x1{\displaystyle x_{1}}

, ..., xN+2{\displaystyle x_{N+2}}

给定，其各次方的幂次也是已知，而f(x1){\displaystyle f(x_{1})}

, ..., f(xN+2){\displaystyle f(x_{N+2})}

也是已知。上式就变成由N+2的线性方程组成的联立方程．有N+2个变数，分别是P0{\displaystyle P_{0}}

, P1{\displaystyle P_{1}}

, ..., PN{\displaystyle P_{N}}

及ε ε -->{\displaystyle \varepsilon }

。可以解出上式的多项式P及误差ε ε -->{\displaystyle \varepsilon }

。下图产生一个在[−1, 1]区间内逼近ex{\displaystyle e^{x}}

的四阶多项式，六个测试点为 −1, −0.7, −0.1, +0.4, +0.9和1。在图中将二端点以外的测试点标示绿色，其误差ε ε -->{\displaystyle \varepsilon }

为 is 4.43 x 10。

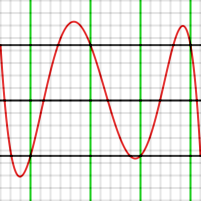
要产生在[−1, 1]区间内逼近ex{\displaystyle e^{x}}

的四阶多项式，依雷米兹算法的第一步计算逼近多项式的误差。垂直的一格为10注意到上图在六个测试点上的误差的确是± ± -->ε ε -->{\displaystyle \pm \varepsilon }

，但极值不是在测试点上。若极值在测试点上（P(x)-f(x)在测试点上有最大值或最小值），在此这个区间的误差都不会超过± ± -->ε ε -->{\displaystyle \pm \varepsilon }

，此多项式即为最佳多项式。雷米兹算法的第二步就是将测试点移到误差函数有最大值或最小值，例如上图中−0.1的测试点需移到−0.28。移动的方式可以进行一轮牛顿法，来取新的测试点位置，由于知道P(x)−f(x)的一阶及二阶导数，因此可以大略计算测试点要移到哪里才能使误差函数的微分为零。计算多项式P(x)的一阶及二阶导数并不困难，但雷米兹算法需要可以计算f(x)的一阶及二阶导数，而且需要很高的精度，其精度需求要比雷米兹算法输出期望的精度要高。在移动测试点后，会产生新的线性联立方程，求解后得到新的多项式，再利用牛顿法去找下一组测试点……，一直到结果收敛到需要的精度为止。雷米兹算法收敛速度很快，对于良态的函数，雷米兹算法是二次收敛，若测试点是在正确位置的10− − -->15{\displaystyle 10^{-15}}

误差范围内，下次测试点是在正确位置的10− − -->30{\displaystyle 10^{-30}}

误差范围内。使用雷米兹算法时，一般会选切比雪夫多项式TN+1{\displaystyle T_{N+1}}