N体问题的数学公式

天体力学中的普遍情况下的N体问题是一组已知初始值的常微分方程组：即已知初始值 q j ( 0 ) , q ˙ ˙ --> j ( 0 ) , j = 1 , … … --> , n {\displaystyle q_{j}(0),\quad {\dot {q}}_{j}(0),j=1,\ldots ,n} （当j 不等于k 时， q j ( 0 ) ≠ ≠ --> q k ( 0 ) {\displaystyle q_{j}(0)\neq q_{k}(0)} ），解出这个二阶常微分方程组

其中 m 1 , m 2 , … … --> m n {\displaystyle m_{1},m_{2},\ldots m_{n}} 是代表n个质点质量的常量。 q 1 , q 2 , … … --> , q n {\displaystyle q_{1},q_{2},\ldots ,q_{n}} 是以时间t为变量描述质点位置的三维矢量函数。

约翰·伯努利已经完全解决了 n = 2 {\displaystyle n=2} 的情况。

一般考虑:解决N体问题

在有关N体问题（ n ≥ ≥ --> 3 {\displaystyle n\geq 3} ）的物理文学作品里有时会发现像“解决N体问题是不可能的”这样的描述。

n 体问题包含6n 个变量，因为每个质点需要3个空间坐标和3个分速度表示。

二体问题

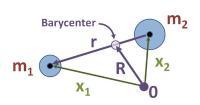
假如两个物体的共同质心是静止的，每一个物体沿着一条圆锥曲线运行，而这条圆锥曲线的焦点与这个系统的质心重合（对于双曲线，是与焦点同侧的那一支）。

假如这两个物体被限制在一起，它们的运动轨迹都为椭圆；这时的势能（经常为一负值）相对于它们离得很远情况在绝对值上大于这个系统总动能（这些物体在它们坐标轴的旋转能这里未计算在内）。

假如它们正在远离，它们将一同沿着抛物线或双曲线运动。

对于双曲线的情况，势能的绝对值小于这个系统的总动能；即两种能量的和为正值。

对于抛物线的情况，两种能量的和为0。当两物体相距很远时，它们的相对速度趋于0。

注释：抛物线轨道的能量为0的事实由当物体相距无限远时，重力势能为0这一假定产生的。系统在无限分离的状态下可以被认为具有任意值（例如42焦）的势能。那一种状态被假定具有0势能（即0焦）。

三体问题

当 n ≥ ≥ --> 3 {\displaystyle n\geq 3} 时的N体问题现在知道得很少。n=3的情况研究得最多，且很多结论可以推广到更大的n。最先尝试解决三体问题是从量化的、寻找显式解的角度。

1767年欧拉找到了共线周期轨道,其中任意质量的三个物体振荡在旋转线上。

1772年拉格朗日发现了一些周期解，存在周期性的扩张和收缩的旋转等边三角形的顶点上。这些解引领了关于中心结构的研究，其中 q ¨ ¨ --> = k q {\displaystyle {\ddot {q}}=kq} （k为大于零的常数）。

三体问题是很令人费解的。它的解可能是混沌的。Charles Delaunay曾经在地-月-日系统做出了主要研究。他曾于1860年和1867年分别出版了长达900页的关于这个问题的著作。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。