历史

1638年，伽利略在《论两种新科学》中以为此线是圆弧。约翰·伯努利参考之前分析过的等时降落轨迹，证明了此线是摆线，并在1696年6月的《博学通报》发表。艾萨克·牛顿、雅各布·伯努利、莱布尼兹和洛必达都得出同一结论，即正确的答案应该是摆线的一段。事实上，约翰·伯努利当时找到的证明方法是错误的。而正确的证法是由他的哥哥雅各布发现的，在他发现以后，伯努利则将其据为己有。除了洛必达的解外，其他人的解都在1697年5月的《博学通报》出现。

证明

约翰·伯努利的证明

费马原理说明，两点间光线传播的路径是所需时间最少的路径。约翰·伯努利利用该原理，通过假设光在光速以恒定竖直加速度（也就是重力加速度g）加速的介质中运动形成的轨迹来导出最速降线。

运用机械能守恒定律，可以导出在恒定重力场中运动的物体的速度满足

式中y表示物体在竖直方向上下落的距离。通过机械能守恒可知，经不同的曲线下落，物体的速度与水平方向的位移无关。 约翰·伯努利注意到，根据折射定律，一束光在密度不均的介质中传播时存在一常数

式中vm为常数，θ为轨迹与竖直方向的夹角，dx为水平方向路径微分，ds为运动方向路径微分。

通过上述方程，我们可以得到两条结论：

在刚开始，当质点的速度为零时，夹角也必然是零。因此，最速降线在起始处与竖直方向相切。

当轨迹变为水平即夹角变为90°时，速度达到最大。

为了简化过程，我们假设质点（或光束）相对于原点(0,0)有坐标(x,y)，且当下落了竖直距离D后达到了最大速度，则

整理折射定律式中的各项并平方得到

可以解得dx对dy有

代入v和vm的表达式得到

这是一个由直径为D的圆所形成的倒过来的摆线的微分方程。

雅各布·伯努利的证明

约翰的哥哥雅各布·伯努利说明了如何从二阶微分得到最短时间的情况。一种现代版本的证明如下。 如果我们从最短时间路径发生微小移动，那么形成三角形满足

dy不变求微分，得到

最后整理得到

最后的部分即二阶微分下距离的改变量与给定的时间的关系。现在考虑下图中的两条相邻路径，中间的水平间隔为dx。对新旧两条路径，改变量为

对于最短时间的路径，两个时间相等，故得到

因此最短时间的情况为

最速降线的数学形式与最短时间

在垂直平面上，自原点 ( 0 , 0 ) {\displaystyle \left(\,0,\,0\right)} 至目的地 ( x 1 , y 1 ) {\displaystyle \left(\,x_{1},\,y_{1}\right)} 的最速降线具有以下数学形式：

x = 1 2 k 2 ( θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> ) ,   y = 1 2 k 2 ( 1 − − --> cos ⁡ ⁡ --> θ θ --> ) . {\displaystyle x={\frac {1}{2}}k^{2}\left(\theta -\sin \theta \right),\ y={\frac {1}{2}}k^{2}\left(1-\cos \theta \right).}

这里的 y {\displaystyle y} 座标轴方向向下，且 y 1 ≥ ≥ --> 0 {\displaystyle y_{1}\geq 0} ； θ θ --> {\displaystyle \theta } 为此摆线参数表达式的参数，原点处 θ θ --> = 0 {\displaystyle \theta =0} 。

物体自原点沿最速降线滑至 θ θ --> = θ θ --> 1 {\displaystyle \theta =\theta _{1}} 处所需的时间可由以下积分式给出：

t = ∫ ∫ --> θ θ --> = 0 θ θ --> = θ θ --> 1 d t = ∫ ∫ --> θ θ --> = 0 θ θ --> = θ θ --> 1 d s v {\displaystyle t=\int _{\theta =0}^{\theta =\theta _{1}}\mathrm {d} t=\int _{\theta =0}^{\theta =\theta _{1}}{\frac {\mathrm {d} s}{v}}} 。

利用 d s = d x 2 + d y 2 {\displaystyle ds={\sqrt {\mathrm {d} x^{2}+\mathrm {d} y^{2}}}} 以及 v = 2 g y {\displaystyle v={\sqrt {2gy}}} ，并以 θ θ --> {\displaystyle \theta } 作为参数，整理后得

d s v = k 2 g d θ θ --> {\displaystyle {\frac {ds}{v}}={\frac {k}{\sqrt {2g}}}\mathrm {d} \theta }

t = k 2 g θ θ --> 1 {\displaystyle t={\frac {k}{\sqrt {2g}}}\theta _{1}} 。

自此摆线的参数式中易知 y {\displaystyle y} 的最大值为 k 2 {\displaystyle k^{2}} ，此值必须等于摆线的绕转圆直径 2 r {\displaystyle 2r} ，因此

k = 2 r {\displaystyle k={\sqrt {2r}}}

t = θ θ --> 1 r g {\displaystyle t=\theta _{1}{\sqrt {\frac {r}{g}}}} 。

现假设终点与原点直线距离   l   {\displaystyle \ l\ } ，且终点对原点的俯角为 ϕ ϕ --> {\displaystyle \phi } 。利用此摆线的参数式，可知

l = x 1 2 + y 1 2 = r ( θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> ) 2 + ( 1 − − --> cos ⁡ ⁡ --> θ θ --> ) 2 {\displaystyle l={\sqrt {x_{1}^{2}+y_{1}^{2}}}=r{\sqrt {\left(\theta -\sin \theta \right)^{2}+\left(1-\cos \theta \right)^{2}}}}

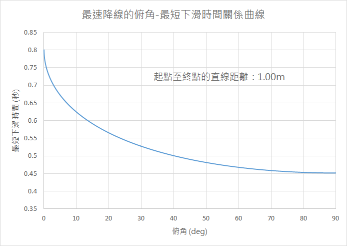
  最速降线问题的终点俯角-最短下滑时间关系曲线。图中原点到终点的直线距离定为1.00米，下滑时间随俯角增大而缩短。

tan ⁡ ⁡ --> ϕ ϕ --> = y 1 x 1 = 1 − − --> cos ⁡ ⁡ --> θ θ --> θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> {\displaystyle \tan \phi ={\frac {y_{1}}{x_{1}}}={\frac {1-\cos \theta }{\theta -\sin \theta }}}

利用 l {\displaystyle l} 的关系式求出 r {\displaystyle r} ，并代回下滑时间中，得

t ( l , θ θ --> ) = l g θ θ --> ( θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> ) 2 + ( 1 − − --> cos ⁡ ⁡ --> θ θ --> ) 2 4 {\displaystyle t\,\left(\,l,\,\theta \right)={\sqrt {\frac {l}{g}}}{\frac {\theta }{\sqrt[{4}]{\left(\theta -\sin \theta \right)^{2}+\left(1-\cos \theta \right)^{2}}}}}

综合上述，讨论在   l   {\displaystyle \ l\ } 已知的情况下，下滑时间 t {\displaystyle t} 与俯角 ϕ ϕ --> {\displaystyle \phi } 的关系为

( ϕ ϕ --> , t ) = ( arctan ⁡ ⁡ --> 1 − − --> cos ⁡ ⁡ --> θ θ --> θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> , l g θ θ --> ( θ θ --> − − --> sin ⁡ ⁡ --> θ θ --> ) 2 + ( 1 − − --> cos ⁡ ⁡ --> θ θ --> ) 2 4 ) {\displaystyle \left(\,\phi ,\,t\right)=\left(\,\arctan {\frac {1-\cos \theta }{\theta -\sin \theta }},\,{\sqrt {\frac {l}{g}}}{\frac {\theta }{\sqrt[{4}]{\left(\theta -\sin \theta \right)^{2}+\left(1-\cos \theta \right)^{2}}}}\right)} 。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。