初等数学用法

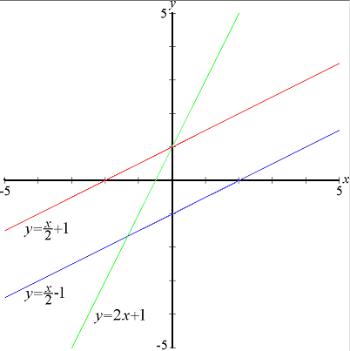
三个线性函数的图形都是直线。红色与蓝色直线的斜率相同。 红色与绿色直线的 y-截距相同。

在初级代数与解析几何， 线性函数 是只拥有一个变数的一阶多项式函数。因为，采用直角坐标系，这些函数的图形是直线，所以，这些函数是 线性的 。线性函数可以表达为 斜截式 ：

其中， k {\displaystyle k\,\!} 是斜率， b {\displaystyle b\,\!} 是 y-截距，函数的图形与 y-轴相交点的 y-坐标。改变斜率 k {\displaystyle k\,\!} 会使直线更陡峭或平缓。改变 y-截距 b {\displaystyle b\,\!} 会将直线移上或移下。

以下三个直线函数的图形展示于图右：

f 1 ( x ) = 2 x + 1 {\displaystyle f_{1}(x)=2x+1\,\!} ，

f 2 ( x ) = x 2 + 1 {\displaystyle f_{2}(x)={\frac {x}{2}}+1\,\!} ，

f 3 ( x ) = x 2 − − --> 1 {\displaystyle f_{3}(x)={\frac {x}{2}}-1\,\!} 。

高等数学用法

在高等数学里， 线性函数 是一个线性映射，是在两个向量空间之间，维持向量加法与标量乘法的映射。

例如，假若，我们用坐标向量 ( coordinate vector 来表示 x {\displaystyle x\,\!} 与 f ( x ) {\displaystyle f(x)\,\!} 。那么，线性函数可以表达为

其中， M {\displaystyle M\,\!} 是矩阵。

参见

仿射变换

等差数列

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。