幻方简史

《系辞》云：“河出图，洛出书，圣人则之。”在宋朝之前，洛书的记述只有文字。

九宫图实物最早发现于西汉，1977年中国考古学家在安徽阜阳县双古堆西汉古墓中发现汉文帝七年（前173年）的太乙九宫占盘，乃是中国汉代幻方的实物。东汉《数术记遗》也有记载。

后来陈抟以降认为河图洛书的洛书代表九宫图，为 1 , … … --> , 9 {\displaystyle 1,\dots ,9} 这 9 {\displaystyle 9} 个数，而 3 {\displaystyle 3} 行、 3 {\displaystyle 3} 列以及两对角线上各自的数之和均为15。

杨辉纵横图

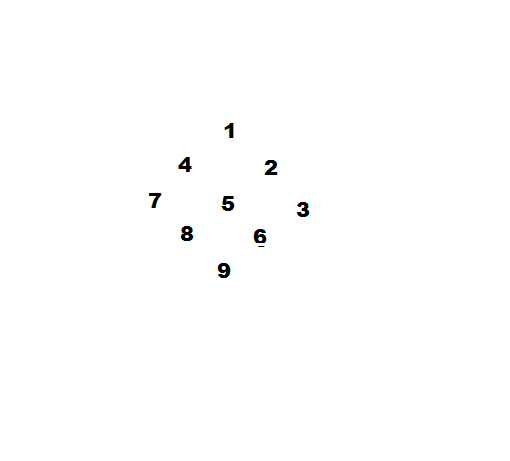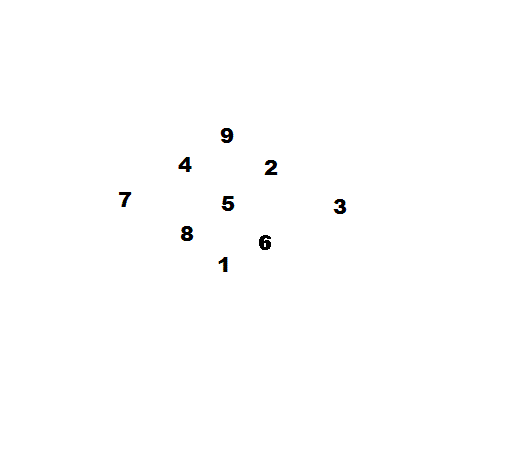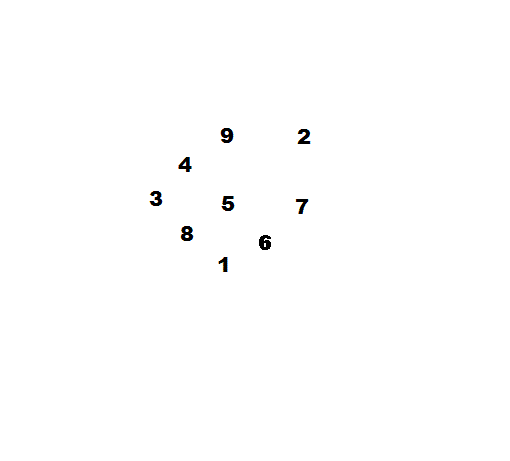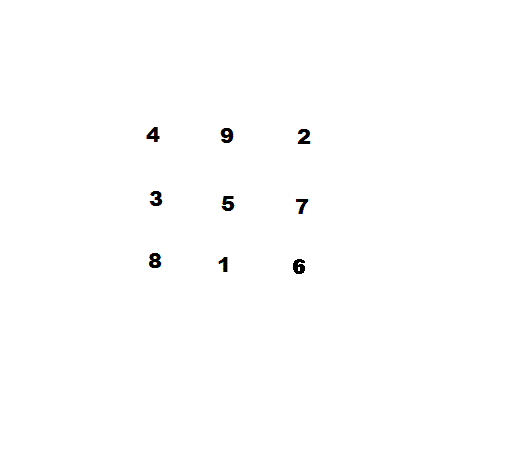
  杨辉纵横图

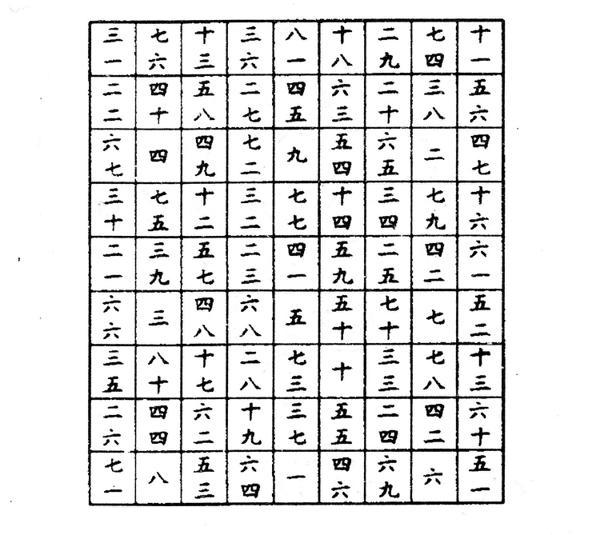
南宋数学家杨辉著《续古摘奇算法》把类似于九宫图的图形命名为纵横图，书中列举3、4、5、6、7、8、9、10阶幻方。其中所述三阶幻方构造法：“九子斜排，上下对易，左右相更，四维挺出，戴九履一，左三右七，二四为肩，六八为足”，比法国数学家Claude Gaspar Bachet提出的方法早三百余年。

构造法

根据构造方法的不同，幻方可以分成三类：奇数阶幻方、 4 M {\displaystyle 4M} 阶幻方和 4 M + 2 {\displaystyle 4M+2} 阶幻方，其中 M {\displaystyle M} 为自然数， 2 {\displaystyle 2} 阶幻方不存在。幻方构造法主要有：连续摆数法、阶梯法（楼梯法）、奇偶数分开的菱形法、对称法、对角线法、比例放大法、斯特雷奇法、LUX法、拉伊尔法（基方、根方合成法）、镶边法、相乘法、幻方模式等。

奇数阶幻方构造法

Siamese方法（Kraitchik 1942年，pp. 148-149）是构造奇数阶幻方的一种方法，说明如下：

把 1 {\displaystyle 1} 放置在第一行的中间。

顺序将 2 , 3 , … … --> {\displaystyle 2,3,\dots } 等数放在右上方格中。

当右上方格出界的时候，则由另一边进入。

当右上方格中已经填有数，则把数填入正下方的方格中。

按照以上步骤直到填写完所有 N 2 {\displaystyle N^{2}} 个方格。

（由于幻方的对称性，也可以把右上改为右下、左上以及左下等方位）

以下图 5 {\displaystyle 5} 阶幻方为例， 1 {\displaystyle 1} 填写在 ( 1 , 3 ) {\displaystyle (1,3)} （第一行第三列）的位置上； 2 {\displaystyle 2} 应当填写在其右上方格即 ( 0 , 4 ) {\displaystyle (0,4)} 中，由于 ( 0 , 4 ) {\displaystyle (0,4)} 超出顶边界，所以从最底行进入，即 ( 5 , 4 ) {\displaystyle (5,4)} ； 3 {\displaystyle 3} 填写在 ( 5 , 4 ) {\displaystyle (5,4)} 的右上方格 ( 4 , 5 ) {\displaystyle (4,5)} 中； 4 {\displaystyle 4} 填写在 ( 4 , 5 ) {\displaystyle (4,5)} 的右上方格 ( 3 , 6 ) {\displaystyle (3,6)} 中，由于 ( 3 , 6 ) {\displaystyle (3,6)} 超出右边界，所以从最左列进入，即 ( 3 , 1 ) {\displaystyle (3,1)} ； 5 {\displaystyle 5} 填写在 ( 3 , 1 ) {\displaystyle (3,1)} 的右上方格 ( 2 , 2 ) {\displaystyle (2,2)} 中； 6 {\displaystyle 6} 应该填写的方格 ( 1 , 3 ) {\displaystyle (1,3)} 已经被 1 {\displaystyle 1} 所占据，因此填写在 ( 2 , 2 ) {\displaystyle (2,2)} 的正下方格 ( 3 , 2 ) {\displaystyle (3,2)} 中；按照上面的步骤直到所有数填入。

魔方阵不是唯一的，比如5阶魔方阵还可以是：

偶数阶幻方构造法

4 M {\displaystyle 4M} 阶幻方构造法

对于 4 M {\displaystyle 4M} 阶幻方一般都用对调法，制作起来很容易。如4阶幻方的排列法：[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] {\displaystyle {\begin{bmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\end{bmatrix}}} 按如上图排列好，再将非主副对角线上的各个数关于中心对调，即成下图：[ 1 15 14 4 12 6 7 9 8 10 11 5 13 3 2 16 ] {\displaystyle {\begin{bmatrix}1&15&14&4\\12&6&7&9\\8&10&11&5\\13&3&2&16\end{bmatrix}}}

4 M + 2 {\displaystyle 4M+2} 阶幻方构造法

加边法

以 6 {\displaystyle 6} 阶为例子，先排出 4 {\displaystyle 4} 阶的幻方，如上图，再将图中每一个数都加上 8 m + 2 = 10 {\displaystyle 8m+2=10} ，有下图：[ 11 25 24 14 22 16 17 19 18 20 21 15 23 13 12 26 ] {\displaystyle {\begin{bmatrix}11&25&24&14\\22&16&17&19\\18&20&21&15\\23&13&12&26\end{bmatrix}}}

结果如下：[ 1 9 34 33 32 2 6 11 25 24 14 31 10 22 16 17 19 27 30 18 20 21 15 7 29 23 13 12 26 8 35 28 3 4 5 36 ] {\displaystyle {\begin{bmatrix}1&9&34&33&32&2\\6&11&25&24&14&31\\10&22&16&17&19&27\\30&18&20&21&15&7\\29&23&13&12&26&8\\35&28&3&4&5&36\end{bmatrix}}}

LUX法

在（4M+2)×(4M+2）个方格的适当格点上，先排出2M+1阶的幻方。在前M+1行的格点，全部标上“L”；在第M+1行的中间格点标上“U”，其余格点标上“L”；在第M+2行的中间格点标上“L”，其余格点标上“U”；在余下的M-1行的格点全部标上“X”。将格点上的数乘以4再减4，再按下面的规则加上1至4其中一个数，填入对应的格上：

例子：

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。