定义与公式

根据高斯磁定律，磁场是螺线矢量场；在空间里任意位置，磁场的散度等于零：

那么，根据亥姆霍兹定理（ Helmholtz theorem ） ，必定存在一个极矢量场 （ polar vector field ） A {\displaystyle \mathbf {A} } ，满足方程

因此，假设 A {\displaystyle \mathbf {A} } 在所有位置都是连续性的、良好定义的，则磁单极子绝对不存在。

又根据安培定律，

其中， μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数， J {\displaystyle \mathbf {J} } 是电流密度。

应用一则矢量恒等式，再采用库仑规范（ Coulomb gauge ）， ∇ ∇ --> ⋅ ⋅ --> A = 0 {\displaystyle \nabla \cdot \mathbf {A} =0} ，可以得到

所以，从安培定律可以推导出电流的泊松方程：

这泊松方程的解为

其中， r {\displaystyle \mathbf {r} } 是场位置， r ′ {\displaystyle \mathbf {r} "} 是源位置， V ′ {\displaystyle \mathbb {V} "} 是体积分的空间， d 3 r ′ {\displaystyle d^{3}\mathbf {r} "} 是微小体元素。

根据法拉第感应定律，

其中， E {\displaystyle \mathbf {E} } 是电场。

重新编排，

所以，在圆括弧内的表达式具有保守性，是某函数 ϕ ϕ --> {\displaystyle \phi }梯度的梯度：

设定 ϕ ϕ --> {\displaystyle \phi } 为电势，重新编排，可以得到电场、电势、磁矢势这三者之间的关系式：

在电动力学和量子力学里，采用拉格朗日表述，拉格朗日量会用到磁矢势 A {\displaystyle \mathbf {A} } 。更详尽细节，请参阅泡利方程、拉格朗日量。

采用国际标准制，磁矢势的单位为伏特·秒／米（volt·second·meter ）。

在电动力学的上下文里，术语矢势和标势分别指的是磁矢势与电势。在数学里，这两个术语有更广义的意义。

规范设定

上述定义并不能唯一地设定磁矢势，因为，添加任意无旋矢量 ∇ ∇ --> λ λ --> {\displaystyle \nabla \lambda } 于磁矢量，不会改变磁场：

因此，磁矢势有一个选择的自由度。这状况称为规范不变性。

采用库仑规范的麦克斯韦方程组

根据高斯定律，

其中， ϵ ϵ --> 0 {\displaystyle \epsilon _{0}} 是电常数。

将方程(2)代入，采用库仑规范， ∇ ∇ --> ⋅ ⋅ --> A = 0 {\displaystyle \nabla \cdot {\textbf {A}}=0} ，可以得到

根据麦克斯韦-安培定律，

将方程(1)、(2)代入，可以得到

所以，麦克斯韦方程组可以写为

库仑规范的优点是，很容易就可以计算出电势，但计算磁矢势比较困难。

采用洛伦茨规范的麦克斯韦方程组

采用洛伦茨规范， A {\displaystyle \mathbf {A} } 必须满足条件

这规范的优点是麦克斯韦方程组可以更简易对称地写为

以达朗贝尔算符 ◻ ◻ --> = d e f ∇ ∇ --> 2 − − --> μ μ --> 0 ϵ ϵ --> 0 ∂ ∂ --> 2 ∂ ∂ --> t 2 {\displaystyle \Box \ {\stackrel {def}{=}}\ \nabla ^{2}-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}} 来表示，

注意到这两个方程的形式为非齐次波动方程，源项目 − − --> ρ ρ --> / ϵ ϵ --> 0 {\displaystyle -\rho /\epsilon _{0}} 、 − − --> μ μ --> 0 J {\displaystyle -\mu _{0}{\textbf {J}}} 在方程右手边。这方程组特别适用于描述电磁波的物理行为。

电磁四维势

在解析狭义相对论问题时，很自然而然地会将磁矢势与电势连结在一起，成为电磁四维势。这样做法主要基于三个动机：

第一、电磁四维势乃是一个四维矢量。使用标准四维矢量变换规则，假若知道在某惯性参考系的电磁四维势，很容易就可以计算出在其它惯性参考系的数值。

第二、经典电磁学的内容可以更简要、更便利地以电磁四维势表达，特别是当采用洛伦茨规范时。

第三、电磁四维势在量子电动力学里占有重要的角色。

电磁四维势定义为

洛伦茨规范以抽象指标记号表示为

其中， ∂ ∂ --> α α --> = d e f ∂ ∂ --> ∂ ∂ --> x α α --> = d e f ( ∂ ∂ --> c ∂ ∂ --> t , ∂ ∂ --> ∂ ∂ --> x 1 , ∂ ∂ --> ∂ ∂ --> x 2 , ∂ ∂ --> ∂ ∂ --> x 3 ) {\displaystyle \partial _{\alpha }\ {\stackrel {def}{=}}\ {\frac {\partial }{\partial x^{\alpha }}}\ {\stackrel {def}{=}}\ \left({\frac {\partial }{c\partial t}},{\frac {\partial }{\partial x^{1}}},{\frac {\partial }{\partial x^{2}}},{\frac {\partial }{\partial x^{3}}}\right)} 是对于反变矢量的偏微分。

麦克斯韦方程组写为

其中， J α α --> = d e f ( ρ ρ --> c , j ) {\displaystyle J^{\alpha }\ {\stackrel {def}{=}}\ (\rho c,\,\mathbf {j} )} 是四维电流密度。

前面谈到电势和磁矢势分别诠释为每单位电荷储存能量和每单位电荷储存动量。这可以从它们的四维矢量观察出来。思考四维动量，它是由能量 E {\displaystyle E} 与动量 p {\displaystyle \mathbf {p} } 共同组成的四维矢量：

改变观测的参考系，四维动量的四个分量会有对应的改变，电磁四维势也会有类似的改变。假若，电磁四维势的电势可以诠释为每单位电荷储存能量，那么，电磁四维势的磁矢势应该也有足够的理由诠释为每单位电荷储存动量。

从源分布计算位势

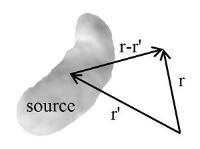
给予在源位置 r ′ {\displaystyle \mathbf {r} "} 的含时电荷分布或含时电流分布，计算在场位置 r {\displaystyle \mathbf {r} } 产生的推迟势。

对于静态的电荷分布和电流分布，电势 ϕ ϕ --> ( r ) {\displaystyle \phi (\mathbf {r} )} 和 磁矢势 A ( r ) {\displaystyle \mathbf {A} (\mathbf {r} )} 分别定义为

其中， r {\displaystyle \mathbf {r} } 是场位置， r ′ {\displaystyle \mathbf {r} "} 是源位置。

在电动力学里，这两个方程必须加以延伸，才能正确地响应含时电流分布或含时电荷分布。定义推迟时间 t r {\displaystyle t_{r}} 为检验时间 t {\displaystyle t} 减去电磁波传播的时间：

其中， c {\displaystyle c} 是光速。

假设，从源位置 r ′ {\displaystyle \mathbf {r} "} 往场位置 r {\displaystyle \mathbf {r} } 发射出一束电磁波，而这束电磁波在检验时间 t {\displaystyle t} 抵达观测者的场位置 r {\displaystyle \mathbf {r} } ，则这束电磁波发射的时间是推迟时间 t r {\displaystyle t_{r}} 。由于电磁波传播于真空的速度是有限的，观测者检验到电磁波的检验时间 t {\displaystyle t} ，会不同于这电磁波发射的推迟时间 t r {\displaystyle t_{r}} 。

推迟标势 ϕ ϕ --> ( r , t ) {\displaystyle \phi (\mathbf {r} ,\,t)} 与 推迟矢势 A ( r , t ) {\displaystyle \mathbf {A} (\mathbf {r} ,\,t)} 分别用方程定义为

请注意，在这两个含时方程内，源电荷密度和源电流密度都跟推迟时间 t r {\displaystyle t_{r}} 有关，而不是与时间无关。

这两个含时方程，是用推理得到的启发式，而不是用任何定律或公理推导出来的。由于讯号以光速传播，从源位置到场位置，需要有限时间，所以在时间 t {\displaystyle t} 的推迟势必定是由在推迟时间 t r {\displaystyle t_{r}} 的源电荷密度或源电流密度产生的。为了要肯定这两个方程的正确性与合理性，这两个方程必须满足非齐次的电磁波方程 。

磁矢势场线图

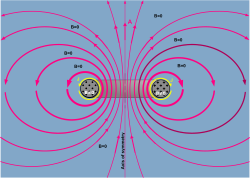
采用库仑规范，一个载有电流密度 J {\displaystyle \mathbf {J} } （黄色）的环形电感器（绘图显示出其截面），其内部（灰色）的磁场 B {\displaystyle \mathbf {B} } （深蓝色）不等与零，其外部（浅蓝色）的磁场等与零。这环形电感器在外部所生成的磁矢势 A {\displaystyle \mathbf {A} } （红色）不等于零，红线越粗代表磁矢势的大小越强。深蓝色圆点表示磁场朝外指出（从显示屏幕指向眼睛）；深蓝色加号表示磁场朝内指入（从眼睛指向显示屏幕）。

关于载流螺线管周围的磁矢势绘图，请参阅理查·费曼的著作 。

在静磁学里，安培方程为 ∇ ∇ --> × × --> B = μ μ --> 0 J {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} } 。这与方程 ∇ ∇ --> × × --> A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ } 很相像。因此，磁场 B {\displaystyle \mathbf {B} } 所生成的磁矢势 A {\displaystyle \mathbf {A} } 的场线，就好似电流密度 μ μ --> 0 J {\displaystyle \mu _{0}\mathbf {J} } 所生成的磁场 B {\displaystyle \mathbf {B} } 场线，所以，在一圈磁通量周围的磁矢势的场线，看起来就好似在一圈电流周围的磁场线。

右图显示出磁矢势的场线。红线越粗代表磁矢势越强（路径越短，磁矢势越强，但是磁矢势的闭合路径积分相同）。

采用库仑规范，磁场的散度和旋度分别为

而磁矢势的散度和旋度分别为

所以，可以将 A {\displaystyle \mathbf {A} } 类比于 B {\displaystyle \mathbf {B} } 。磁矢势的源头是磁场，就如同磁场的源头是电流。

历史

麦可·法拉第最先提出电紧张态的概念。在研究电磁感应理论时，他发现当将物体放在磁铁或电流的附近时，物体会进入一种状态。假若不打扰这系统，则处于此状态的物体不会自发地显示出任何现象。但是，一当系统有所变化，像磁铁被移动了，或电流被增大了，则这状态也会改变，因而产生电流或趋向产生电流。法拉第称此状态为“电紧张态”。但是，这概念并没有被很明确地说明。

后来，开尔文男爵于1851年引入磁矢势的概念，并且给定磁矢势与磁场之间的关系：

在论文《论法拉第力线》的后半部分，麦克斯韦开始仔细分析电紧张态的物理性质。他给出一条重要定律：作用于一个导体的微小元素的电场，可以由该微小元素的电紧张态对于时间的导数来衡量。 以现代标记表示，这方程为

这是麦克斯韦学术生涯中的第一个重要突破，他将法拉第的电紧张态辨识为开尔文男爵的磁矢势，并且对于电紧张态给出严格定义。

对于电紧张态的定义式取旋度，则可得到法拉第感应方程：

麦克斯韦在他的论文里特别提出，开尔文男爵于1851年发现的关于磁矢势的数学性质， 即任意添加一个函数的梯度给磁矢势，都不会改变磁矢势与磁场的关系式、法拉第感应方程，这数学性质后来演化为现今规范自由的概念。

相关条目

磁标势

参考文献

Duffin, W.J. Electricity and Magnetism, Fourth Edition. McGraw-Hill. 1990.

Jackson, John Davd, Classical Electrodynamics 3rd, John-Wiley, 1999, ISBN 047130932X

Kraus, John D., Electromagnetics 3rd, McGraw-Hill, 1984, ISBN 0070354235

Ulaby, Fawwaz. Fundamentals of Applied Electromagnetics, Fifth Edition. Pearson Prentice Hall. 2007: 226–228. ISBN 0-13-241326-4.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。