理论

任何两种相接触的固体的费米能级（Fermi level，或者严格意义上，化学势）必须相等。 费米能级和真空能级的差值称作功函数。接触金属和半导体具有不同的功函数，分别记为 ϕ ϕ --> M {\displaystyle \phi _{M}} 和 ϕ ϕ --> S {\displaystyle \phi _{S}} 。当两种材料相接触时，电子将会从 低功函（高Fermi level） 一边流向另一边直到费米能级相平衡。从而， 低功函（高Fermi level） 的材料将带有少量正电荷而 高功函（低Fermi level） 材料则会变得具有少量电负性。最终得到的静电势称为 内建场 记为 V b i {\displaystyle V_{bi}} 。这种 接触电势 将会在任何两种固体间出现并且是诸如二极管整流现象和温差电效应等的潜在原因。内建场是导致半导体连接处 能带弯曲 的原因。明显的能带弯曲在金属中不会出现因为他们很短的屏蔽长度意味着任何电场只在接触面间无限小距离内存在。

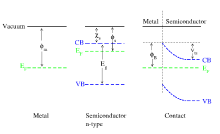
欧姆接触或肖特基势垒形成于金属与n型半导体相接触。

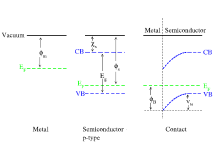
欧姆接触或肖特基势垒形成于金属与p型半导体相接触。

在经典物理图像中，为了克服势垒，半导体载流子必须获得足够的能量才能从费米能级跳到弯曲的导带顶。穿越势垒所需的能量 ϕ ϕ --> B {\displaystyle \phi _{B}} 是内建势及费米能级与导带间偏移的总和。同样对于n型半导体， ϕ ϕ --> B = ϕ ϕ --> M − − --> χ χ --> S {\displaystyle \phi _{B}=\phi _{M}-\chi _{S}} 当中 χ χ --> S {\displaystyle \chi _{S}} 是半导体的电子亲合能（electron 导带finity），定义为真空能级和导带（CB）能级的差。对于p型半导体， ϕ ϕ --> B = E g − − --> ( ϕ ϕ --> M − − --> χ χ --> S ) {\displaystyle \phi _{B}=E_{g}-(\phi _{M}-\chi _{S})} 其中 E g {\displaystyle E_{g}} 是禁带宽度。当穿越势垒的激发是热力学的，这一过程称为热发射。真实的接触中一个同等重要的过程既即为量子力学隧穿。WKB近似描述了最简单的包括势垒穿透几率与势垒高度和厚度的乘积指数相关的隧穿图像。对于电接触的情形， 耗尽区宽度 决定了厚度，其和内建场穿透入半导体内部长度同量级。泊松层宽度 W {\displaystyle W} 可以通过解泊松方程以及考虑半导体内存在的掺杂来计算:

在MKS单位制 ρ ρ --> {\displaystyle \rho } 是净电荷密度而 ϵ ϵ --> {\displaystyle \epsilon } 是介电常数。几何结构是一维的因为界面被假设为平面的。对方程作一次积分，我们得到

积分常数 C 0 = − − --> ρ ρ --> W ϵ ϵ --> {\displaystyle C_{0}={\frac {-\rho W}{\epsilon }}} 根据耗尽层定义为界面完全被屏蔽的长度。就有

其中 V ( 0 ) = V b i {\displaystyle V(0)=V_{bi}} 被用于调整剩下的积分常数。这一 V ( x ) {\displaystyle V(x)} 方程描述了插图右手边蓝色的断点曲线。耗尽宽度可以通过设置 V ( W ) = 0 {\displaystyle V(W)=0} 来决定，结果为

对于0 < x = e N d o p a n t {\displaystyle \rho =eN_{dopant}} 是完全 耗尽 的半导体中离子化的施主和受主净电荷密度 N d o p a n t {\displaystyle N_{dopant}} 以及 e {\displaystyle e} 是电荷。 ρ ρ --> {\displaystyle \rho } 和 V b i {\displaystyle V_{bi}} 对于n型半导体取正号而对于p型半导体取负号，n型的正曲率 V ″ ( x ) {\displaystyle V""(x)} 和p型的负曲率如图所示。

从这个大概的推导中可注意到势垒高度（与电子亲和性和内建场相关）和势垒厚度（和内建场、半导体绝缘常数和掺杂密度相关）只能通过改变金属或者改变掺杂密度来改变。总之工程师会选择导电、非反应、热力学稳定、电学性质稳定且低张力的接触金属然后提高接触金属下方区域掺杂密度来减小势垒高度差。高掺杂区依据掺杂种类被称为 n + {\displaystyle n^{+}} 或者 p + {\displaystyle p^{+}} 。因为在隧穿中透射系数与粒子质量指数相关，低有效质量的半导体更容易被解除。另外，小禁带半导体更容易形成欧姆接触因为它们的电子亲和度（从而势垒高度）更低。

上述简单的理论预言了 ϕ ϕ --> B = ϕ ϕ --> M − − --> χ χ --> S {\displaystyle \phi _{B}=\phi _{M}-\chi _{S}} ，因此似乎可以天真的认为功函靠近半导体的电子亲和性的金属通常应该容易形成欧姆接触。事实上，高功函金属可以形成最好的p型半导体接触而低工函金属可以形成最好的n型半导体接触。不幸的是实验表明理论模型的预测能力并不比上述论断前进更远。在真实条件下，接触金属会和半导体表面反应形成具有新电学性质的复合物。界面处一层污染层会非常有效的增加势垒宽度。半导体表面可能会重构成一个新的电学态。接触电阻与界面间化学细节的相关性是导致欧姆接触制造工艺可重复性为如此巨大的制造挑战的原因。

实验特性

特征接触电阻 实验上定义为J-V曲线在V=0处的斜率，J是电流密度:

接触电阻的单位因此成为 Ω Ω --> − − --> c m 2 {\displaystyle \Omega -cm^{2}} ，其中 Ω Ω --> {\displaystyle \Omega 欧姆 代表电阻单位欧姆。

接触电阻可以通过比较比较带有欧姆表的 四探针 测量（four-probe measurement）和简单的两探针测量结果来粗略估计。在两探针测量中，测量电流导致同时跨越探针和接触的势降，从而这些元件的电阻与真是元间的电阻是串联而不可分离的。在四探针测量中，一对探针用于注入测量电流同时另一对并联的探针用于测量跨越器件的势降。在四探针情形下，没有通过电压测量探针的势降因而接触电阻降并不包括其中。从两极法和四极法推导的电阻差值是对接触电阻合理准确的测量假设探针电阻足够小而忽略不计。特性接触电阻可以通过乘以接触面积来得到。

随着集成电路制备过程的发展，远更复杂的接触电阻测量被使用，最流行的方法即为传输线测量）（transmission line measurement）。传输线测量的基本思路是描绘类似接触之间同宽不同长度的条状电阻值。结果曲线的斜率是块状薄膜电阻率（resistivity）的函数而截距即为接触电阻（resistance）。

欧姆接触的制备

欧姆接触制备是材料工程里研究很充分而不太有未知剩余的部分。可重复且可靠的接触制备需要极度洁净的半导体表面。例如，因为 天然氧化物 会迅速在硅表面形成，接触的性能会十分敏感地取决于制备准备的细节。

接触制备的基础步骤是半导体表面清洁、接触金属沉积、图案制造和退火。表面清洁可以通过溅射蚀刻、化学蚀刻、反应气体蚀刻或者离子研磨。比如说，硅的天然氧化物可以通过蘸氢氟酸（HF）来去除，而砷化镓（GaAs）则更具代表性的通过蘸溴化甲醇来清洁。清洁过后金属通过溅射、蒸发沉积或者化学气相沉积（CVD）沉积下来。溅射是金属沉积中比蒸发沉积更快且更方便方法但是等离子带来的离子轰击可能会减少表面态或者甚至颠倒表面电荷载流子的类型。正因为此更为平和且依然快速的CVD是更加为人所倾向的方法。接触的图案制造是通过标准平版照相术来完成的，比如 剥落 中接触金属是通过沉积于光刻胶层孔洞之中并稍后取出光刻胶来完成的。沉积后接触的退火能有效去除张力并引发有利的金属和半导体之间的反应。

技术角度上重要的接触类型

现代对硅的欧姆接触比如二硅化钛钨通常是CVD制作的硅化物。接触通常通过沉积过渡金属然后退火形成硅化物来制造且形成的硅化物通常为非化学计算的。硅化物接触也可通过直接溅射复合或者离子移植过渡金属来沉积并退火。铝是另一种可同时用于n型和p型半导体重要的硅接触金属，但并非所有n型硅和铝都可以形成欧姆接触，一般而言，n+型硅和铝较能形成良好的欧姆接触，与n型或n-型硅则形成schottky接触，而一般n型硅，掺杂浓度在10 cm 左右，先镀Ti接触硅再镀上Ag形成欧姆接触。连同使用其它的反应金属，铝接触通过消耗天然氧化物中的氧来形成。硅化物很大程度上取代了铝（Al）部分因为高折射材料不太倾向于扩散到不希望的地带，特别是在随后的高温处理过程中。

复合半导体接触的形成可以理解比硅接触更为复杂。比如说，砷化镓（GaAs）表面倾向于丢失砷而且这种砷丢失的趋势可以通过沉积金属而被可观的放大。另外，砷的易挥发性限制了沉积后退火时砷化镓器件的承受度。砷化镓及其他复合半导体的一种解决办法是沉积低禁带合金接触层与高掺杂层相对。例如，砷化镓自己比砷化铝镓（AlGaAs）有更小的禁带带宽 所以一层靠近它表面的砷化镓层能促进欧姆行为。总之相比之下，III-V和II-VI半导体欧姆接触技术比硅欧姆接触技术发展较缓。

透明或半透明接触对于主动矩阵液晶显示器LCD、光电器件诸如激光二极管（LD）、发光二极管（LED）及光电管是必要的。最流行的选择是氧化铟锡（ITO），一种通过在氧气环境下溅射铟-锡（In-Sn）靶形成的金属。

重要性

接触电阻相关联的RC时间常数会限制器件的频率响应。引线电阻的充电与放电高时钟速率的数字电子设备能量耗散的主要原因。接触电阻在非常见半导体制成的低频和模拟电路中通过焦耳热的形式导致能量耗散（比如太阳能电池）。金属接触制备方法的建立是任何新兴半导体科技发展的重要部分。金属接触的电迁移与分离成层也是电子器件寿命的限制因素之一。

参考资料

Sze, S.M. Physics of Semiconductor Devices . John Wiley & Sons. 1981. ISBN 978-0-471-05661-4. Discussion of theory plus device implications.

Zangwill, Andrew. Physics at Surfaces. Cambridge University Press. 1988. ISBN 978-0-521-34752-5. Approaches接触from point of view of surface states and reconstruction.

参见

TheAmerican Vacuum Societyhas an excellent接触short courseon this topic.

Journal of the American Vacuum Society、Thin Solid FilmsandJournal of the Electrochemical Societyare journals that publish current research on欧姆contacts.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。