Z变换
历史
现在所知的Z变换的基本思想,拉普拉斯就已了解,而1947年 W. Hurewicz ( 英语 : Witold Hurewicz ) 用作求解常系数差分方程的一种容易处理的方式。 后来由1952年哥伦比亚大学的采样控制组的雷加基尼和查德称其为“Z变换”。
E. I. Jury后来发展并推广了改进或 高级Z变换 ( 英语 : Advanced Z-transform ) 。
Z变换中包含的思想在数学里称作母函数方法,该方法可以追溯到1730年的时候,棣莫弗与概率论结合将其引入。 从数学的角度,当把数字序列视为解析函数的(洛朗)展开时,Z变换也可以看成是洛朗级数。
定义
像很多积分变换一样,Z变换可以有单边和双边定义。
双边Z变换
双边 Z变换把离散时域信号 x[n] 转为形式幂级数 X(Z) 。
当中 n {\displaystyle n} 是整数, z {\displaystyle z} 是复数变量,其表示方式为
其中 A 为 z 的模, j 为虚数单位,而 ɸ 为 幅角 (也叫 相位角 ),用弧度表示。
单边Z变换
另外,只对 n ≥ 0 定义的 x[n] , 单边 Z变换定义为
在信号处理中,这个定义可以用来计算离散时间因果系统的单位冲激响应。
单边Z变换的一个重要例子是概率母函数,其中 x[n] 部分是离散随机变量取 n 值时的概率,而函数 X(z) 通常写作 X(s) ,用 s = z 表示。Z变换的性质(在下面)在概率论背景下有很多有用的解释。
地球物理学定义
地球物理中的Z变换,通常的定义是 z 的幂级数而非 z 的。例如,Robinson、Treitel 和Kanasewich都使用这个惯例。 地球物理定义为:
这两个定义是等价的;但差分结果会有一些不同。例如,零点和极点的位置移动在单位圆内使用一个定义,在单位圆外用另一个定义。 因此,需要注意特定作者使用的定义。
逆Z变换
逆 Z变换为
其中 C 是完于收敛域(ROC)内的包围原点的一个逆时针闭合路径。在 ROC 是因果的情况下(参见例2),这意味着路径 C 必须包围 X(z) 的所有极点。
这个曲线积分的一个特殊情形出现在 C 是单位圆的时候(可以在ROC包含单位圆的时候使用,总能保证 X(z) 是稳定的,即所有极点都在单位圆内)。逆Z变换可以化简为逆离散傅里叶变换:
有限范围 n 和有限数量的均匀间隔的 z 值的Z变换可以用Bluestein的FFT算法方便地计算。离散时间傅里叶变换(DTFT)—不要与离散傅里叶变换(DFT)混淆—是通过将 z 限制在位于单位圆上而得到的一种Z变换的特殊情况。
收敛域
收敛域(ROC)是指Z变换的求和收敛的复平面上的点集。
例1(无ROC)
令 x[n] = (0.5) 。在区间 (−∞, ∞) 上展开 x[n] 成为
观察上面的和
因此,没有一个 z 值可以满足这个条件。
例2(因果ROC)
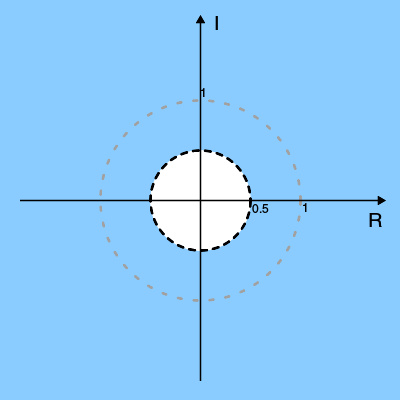
ROC用蓝色表示,单位圆用灰色虚点圆表示(外圈者,而 | z | = 0.5 这个圆用虚线圆表示(内圈者)
令 x [ n ] = 0.5 n u [ n ] {\displaystyle x[n]=0.5^{n}u[n]\ } (其中 u 是单位阶跃函数)。在区间 (−∞, ∞) 上展开 x[n] 得到
观察这个和
最后一个等式来自无穷几何级数,而等式仅在 |0.5 z | 0.5。因此,收敛域为 | z | > 0.5。在这种情况下,收敛域为复平面“挖掉”原点为中心的半径为 0.5 的圆盘。
例3(非因果ROC)
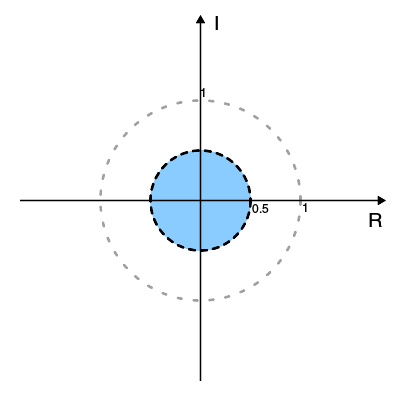
ROC用蓝色表示,单位圆用灰色虚点圆表示(用眼睛看会呈红色),而 | z | = 0.5 这个圆用虚线圆表示
令 x [ n ] = − − --> ( 0.5 ) n u [ − − --> n − − --> 1 ] {\displaystyle x[n]=-(0.5)^{n}u[-n-1]\ } (其中 u 是单位阶跃函数)。在区间 (−∞, ∞) 上展开 x[n] 得到
观察这个和
再次使用无穷几何级数,此等式只在 |0.5 z | < 1 时成立,可以用 z 为变量写成 | z | < 0.5。因此,收敛域为 | z | < 0.5。在这种情况下,收敛域为中心在原点的半径为 0.5 的圆盘。
本例与上例的不同之处 仅在 收敛域上。这是意图展示只有变换结果是不够的。
实例结论
实例2和3清楚地表明,当且仅当指定收敛域时, x[n] 的Z变换 X(z) 才是唯一的。画因果和非因果情形的 零极点图 ( 英语 : pole–zero plot ) 表明,在这两种情况下收敛域都不包含极点位于 0.5 的情形。这可以拓展到多个极点的情形:收敛域 永远不会 包含极点。
在例2中,因果系统产生一个包含 | z | = ∞ 的收敛域,而例3中的非因果系统产生包含 | z | = 0 的收敛域。
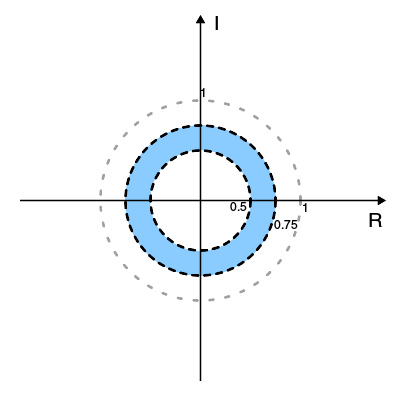
ROC表示为蓝色圆环 0.5 z|在有多个极点的系统中,收敛域可以既不包含 | z | = ∞ 也不包含 | z | = 0。画出的收敛域与一个圆形带。例如,x [ n ] = 0.5 n u [ n ] − − --> 0.75 n u [ − − --> n − − --> 1 ] {\displaystyle x[n]=0.5^{n}u[n]-0.75^{n}u[-n-1]} 的极点为 0.5 与 0.75。收敛域会是 0.5 < | z | 0.5 包含单位圆。如果给定一个没有收敛域的Z变换(即模糊的 x[n] ),可以确定一个唯一的 x[n] 满足下列:如果你要稳定性,收敛域必须包含单位圆;如果你需要一个因果系统,收敛域必须包含无穷大,并且系统函数应为一个右边序列。如果你需要一个非因果系统,那么收敛域必须包含原点,且系统函数为左边序列。如果你既要稳定性,也要因果性,系统函数的所有极点都必须在单位圆内。可以找到唯一的 x[n] 。性质 帕塞瓦尔定理∑ ∑ --> n = − − --> ∞ ∞ --> ∞ ∞ --> x 1 [ n ] x 2 ∗ ∗ --> [ n ] = 1 j 2 π π --> ∮ C X 1 ( v ) X 2 ∗ ∗ --> ( 1 v ∗ ∗ --> ) v − − --> 1 d v {\displaystyle \sum _{n=-\infty }^{\infty }x_{1}[n]x_{2}^{*}[n]\quad =\quad {\frac {1}{j2\pi }}\oint _{C}X_{1}(v)X_{2}^{*}({\tfrac {1}{v^{*}}})v^{-1}\mathrm {d} v} 初值定理 :如果 x [ n ] 为因果的,那么x [ 0 ] = lim z → → --> ∞ ∞ --> X ( z ) . {\displaystyle x[0]=\lim _{z\to \infty }X(z).} 终值定理 :如果 ( z −1) X ( z ) 的极点在单位圆内,则x [ ∞ ∞ --> ] = lim z → → --> 1 ( z − − --> 1 ) X ( z ) . {\displaystyle x[\infty ]=\lim _{z\to 1}(z-1)X(z).} 常见的Z变换对表 这里:u : n ↦ ↦ --> u [ n ] = { 1 , n ≥ ≥ --> 0 0 , n < 0 {\displaystyle u:n\mapsto u[n]={\begin{cases}1,&n\geq 0\\0,&n : n ↦ ↦ --> δ δ --> [ n ] = { 1 , n = 0 0 , n ≠ ≠ --> 0 {\displaystyle \delta :n\mapsto \delta [n]={\begin{cases}1,&n=0\\0,&n\neq 0\end{cases}}} 是离散时间单位冲激函数。两者通常都不认为是真正的函数,但由于它们的不连续性把它们看成是分布(它们在 n = 0 处的值通常无关紧要,除非在处理离散时间的时候,它们会变成衰减离散级数;在本章节中对连续和离散时间域,都在 n = 0 处取 1,否则不能使用下表中收敛域一栏的内容)。同时列出两个“函数”,使得(在连续时间域)单位阶跃函数是单位冲激函数的积分,或(在离散时间域)单位阶跃函数是单位冲激函数的求和,因此要令他们的值在 n = 0 处为 1。与傅里叶级数和傅里叶变换的关系 对于区域 |z|=1(称为单位圆)内的 z 值,我们可以通过定义 z=e 来用单一实变量的函数来表示该变换。于是双边变换就简化为了傅里叶级数: 也被称作 x[n] 序列的离散时间傅里叶变换(DTFT)。这个以 2π 为周期的函数是傅里叶变换的 周期性求和 ( 英语 : periodic summation ) ,这使得它成为广泛使用的分析工具。要理解这一点,令 X(f) 为任意函数 x(t) 的傅里叶变换,该函数以某个间隔 T 采样就与 x[n] 序列相等。于是 x[n] 序列的DTFT可以写作:∑ ∑ --> n = − − --> ∞ ∞ --> ∞ ∞ --> x ( n T ) ⏞ ⏞ --> x [ n ] e − − --> j 2 π π --> f n T ⏟ ⏟ --> DTFT = 1 T ∑ ∑ --> k = − − --> ∞ ∞ --> ∞ ∞ --> X ( f − − --> k / T ) . {\displaystyle \underbrace {\sum _{n=-\infty }^{\infty }\overbrace {x(nT)} ^{x[n]}\ e^{-j2\pi fnT}} _{\text{DTFT}}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }X(f-k/T).} 若T的单位是秒, f {\displaystyle \textstyle f} 的单位即为赫兹。比较两个数列可得 ω ω --> = 2 π π --> f T {\displaystyle \textstyle \omega =2\pi fT} 为 标准化频率 ( 英语 : Normalized frequency (digital signal processing)#Alternative normalizations ) ,单位是radians per sample。数值ω=2π对应 f = 1 T {\displaystyle \textstyle f={\frac {1}{T}}} Hz. ,而且在替换 f = ω ω --> 2 π π --> T , {\displaystyle \textstyle f={\frac {\omega }{2\pi T}},} 后, Eq.1 可以表示为傅里叶变换X(•) : ∑ ∑ --> n = − − --> ∞ ∞ --> ∞ ∞ --> x [ n ] e − − --> j ω ω --> n = 1 T ∑ ∑ --> k = − − --> ∞ ∞ --> ∞ ∞ --> X ( ω ω --> 2 π π --> T − − --> k T ) ⏟ ⏟ --> X ( ω ω --> − − --> 2 π π --> k 2 π π --> T ) . {\displaystyle \sum _{n=-\infty }^{\infty }x[n]\ e^{-j\omega n}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }\underbrace {X\left({\tfrac {\omega }{2\pi T}}-{\tfrac {k}{T}}\right)} _{X\left({\frac {\omega -2\pi k}{2\pi T}}\right)}.} 若数列x(nT)表示线性时不变系统的冲激响应,这些函数也称为频率响应,当x(nT)是周期性数列,其DTFT在一或多个共振频率发散,在其他频率均为零。这一般会用在共振频率,振幅可变的狄拉克δ函数表示。因为其周期性,只会有有限个振幅,可以用较简单许多的离散傅里叶变换来计算。(参照离散傅里叶变换#周期性)和拉氏变换的关系 双线性变换 双线性变换可以用在连续时间滤波器(用拉氏域表示)和离散时间滤波器(用Z域表示)之间的变换,其变换关系如下:s = 2 T ( z − − --> 1 ) ( z + 1 ) {\displaystyle s={\frac {2}{T}}{\frac {(z-1)}{(z+1)}}} 将一个拉氏域的函数 H ( s ) {\displaystyle H(s)} 变换为Z域下的 H ( z ) {\displaystyle H(z)} ,或是z = 2 + s T 2 − − --> s T {\displaystyle z={\frac {2+sT}{2-sT}}} 从Z域变换到拉氏域。借由双线性变换,复数的s平面(拉氏变换)可以映射到复数的z平面(Z变换)。这个变换是非线性的,可以将S平面的整个 j Ω轴映射到Z平面的单位圆内。因此,傅里叶变换(在 j Ω axis计算的拉氏变换)变成离散时间傅里叶变换,前提是假设其傅里叶变换存在,也就是拉氏变换的收敛区域包括 j Ω轴。线性常系数差分方程 线性常系数差分(LCCD)方程是基于自回归滑动平均的线性系统表达形式。∑ ∑ --> p = 0 N y [ n − − --> p ] α α --> p = ∑ ∑ --> q = 0 M x [ n − − --> q ] β β --> q {\displaystyle \sum _{p=0}^{N}y[n-p]\alpha _{p}=\sum _{q=0}^{M}x[n-q]\beta _{q}} 上面等式两边可以同时除以 α 0 ,如果非零,正规化 α 0 = 1,LCCD方程可以写成y [ n ] = ∑ ∑ --> q = 0 M x [ n − − --> q ] β β --> q − − --> ∑ ∑ --> p = 1 N y [ n − − --> p ] α α --> p . {\displaystyle y[n]=\sum _{q=0}^{M}x[n-q]\beta _{q}-\sum _{p=1}^{N}y[n-p]\alpha _{p}.} LCCD方程的这种形式有利于更加明确“当前”输出 y[n] 是过去输出 y[n−p] 、当前输入 x[n] 与之前输入 x[n−q] 的一个函数。传递函数 对上述方程去Z变换(使用线性和时移法则)得到Y ( z ) ∑ ∑ --> p = 0 N z − − --> p α α --> p = X ( z ) ∑ ∑ --> q = 0 M z − − --> q β β --> q {\displaystyle Y(z)\sum _{p=0}^{N}z^{-p}\alpha _{p}=X(z)\sum _{q=0}^{M}z^{-q}\beta _{q}} 整理结果H ( z ) = Y ( z ) X ( z ) = ∑ ∑ --> q = 0 M z − − --> q β β --> q ∑ ∑ --> p = 0 N z − − --> p α α --> p = β β --> 0 + z − − --> 1 β β --> 1 + z − − --> 2 β β --> 2 + ⋯ ⋯ --> + z − − --> M β β --> M α α --> 0 + z − − --> 1 α α --> 1 + z − − --> 2 α α --> 2 + ⋯ ⋯ --> + z − − --> N α α --> N . {\displaystyle H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{q=0}^{M}z^{-q}\beta _{q}}{\sum _{p=0}^{N}z^{-p}\alpha _{p}}}={\frac {\beta _{0}+z^{-1}\beta _{1}+z^{-2}\beta _{2}+\cdots +z^{-M}\beta _{M}}{\alpha _{0}+z^{-1}\alpha _{1}+z^{-2}\alpha _{2}+\cdots +z^{-N}\alpha _{N}}}.} 零点和极点 由代数基本定理得知分子有 M 个根(对应于 H 的零点)和分母有 N 个根(对应于极点)。用极点和零点重新整理传递函数为H ( z ) = ( 1 − − --> q 1 z − − --> 1 ) ( 1 − − --> q 2 z − − --> 1 ) ⋯ ⋯ --> ( 1 − − --> q M z − − --> 1 ) ( 1 − − --> p 1 z − − --> 1 ) ( 1 − − --> p 2 z − − --> 1 ) ⋯ ⋯ --> ( 1 − − --> p N z − − --> 1 ) {\displaystyle H(z)={\frac {(1-q_{1}z^{-1})(1-q_{2}z^{-1})\cdots (1-q_{M}z^{-1})}{(1-p_{1}z^{-1})(1-p_{2}z^{-1})\cdots (1-p_{N}z^{-1})}}} 其中 q k 为 k 阶零点, p k 为 k 阶极点。零点和极点通常是复数,当在复平面(z平面)作图时称为 零极点图 ( 英语 : pole–zero plot ) 。此外,在 z = 0 和 z = ∞ 也可能存在零点和极点。如果我们把这些极点和零点以及高阶零点和极点考虑在内的话,零点和极点的数目总会相等。通过对分母因式分解,可以使用部分分式分解可以转换回时域。这样做会导出系统的冲激响应和线性常系数差分方程。输出响应 如果一个系统 H(z) 由信号 X(z) 驱动,那么输出为 Y(z) = H(z)X(z) 。通过对 Y(z) 部分分式分解并取逆Z变换可以得到输出 y[n] 。在实际运用中,在分式分解 Y ( z ) z {\displaystyle {\frac {Y(z)}{z}}} 之后再乘 z 产生 Y(z) 的一个形式(含有很容易计算逆Z变换的项)往往很有用。参见 延伸阅读 外部链接
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

相关资料

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
知识互答
关于我们

APP下载


























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}