基本定义

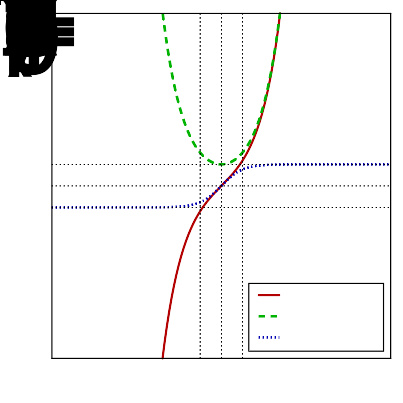
sinh , cosh 和 tanh

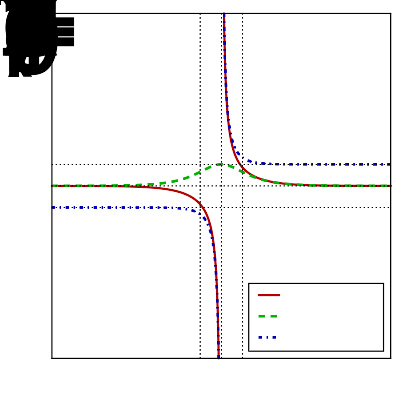
csch , sech 和 coth

sinh ⁡ ⁡ --> x = e x − − --> e − − --> x 2 {\displaystyle \sinh x={{e^{x}-e^{-x}} \over 2}}

cosh ⁡ ⁡ --> x = e x + e − − --> x 2 {\displaystyle \cosh x={{e^{x}+e^{-x}} \over 2}}

tanh ⁡ ⁡ --> x = sinh ⁡ ⁡ --> x cosh ⁡ ⁡ --> x {\displaystyle \tanh x={{\sinh x} \over {\cosh x}}}

coth ⁡ ⁡ --> x = 1 tanh ⁡ ⁡ --> x {\displaystyle \coth x={1 \over {\tanh x}}}

s e c h x = 1 cosh ⁡ ⁡ --> x {\displaystyle {\mathop {\rm {sech}}}x={1 \over {\cosh x}}}

c s c h x = 1 sinh ⁡ ⁡ --> x {\displaystyle {\mathop {\rm {csch}}}x={1 \over {\sinh x}}}

函数 cosh ⁡ ⁡ --> x {\displaystyle \cosh x\!} 是关于 y 轴对称的偶函数。函数 sinh ⁡ ⁡ --> x {\displaystyle \sinh x\!} 是奇函数。

如同当 t {\displaystyle t} 遍历实数集 R {\displaystyle \mathbb {R} } 时，点（ cos ⁡ ⁡ --> t {\displaystyle \cos t\!} , sin ⁡ ⁡ --> t {\displaystyle \sin t\!} ）的轨迹是一个圆 x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} 一样，当 t {\displaystyle t} 遍历实数集 R {\displaystyle \mathbb {R} } 时，点（ cosh ⁡ ⁡ --> t {\displaystyle \cosh t\!} , sinh ⁡ ⁡ --> t {\displaystyle \sinh t\!} ）的轨迹是单位双曲线 x 2 − − --> y 2 = 1 {\displaystyle x^{2}-y^{2}=1} 的右半边。这是因为有以下的恒等式：

参数 t 不是圆角而是双曲角，它表示在 x 轴和连接原点和双曲线上的点（ cosh ⁡ ⁡ --> t {\displaystyle \cosh t\!} , sinh ⁡ ⁡ --> t {\displaystyle \sinh t\!} ）的直线之间的面积的两倍。

历史

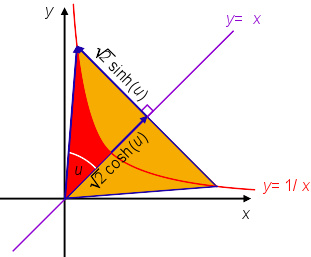
在直角双曲线(方程 y = 1/ x )下，双曲线三角形(黄色)，和对应于双曲角 u 的双曲线扇形(红色)。这个三角形的边分别是双曲函数中cosh和sinh的√2倍。

在18世纪，约翰·海因里希·兰伯特介入了双曲函数 ，并计算了双曲几何中双曲三角形的面积 。自然对数函数是在直角双曲线 x y = 1 {\displaystyle xy=1} 下定义的，可构造双曲线直角三角形，底边在线 y = x {\displaystyle y=x} 上，一个顶点是原点，另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数，是自然对数的逆函数指数函数，即要形成指定双曲角 u ，在渐进线即x或y轴上需要有的x或y的值。显见这里的底边是 ( e u + e − − --> u ) 2 2 {\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}} ，垂线是 ( e u − − --> e − − --> u ) 2 2 {\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}} 。

通过旋转和缩小线性变换，得到单位双曲线下的情况，有：

cosh ⁡ ⁡ --> u = e u + e − − --> u 2 {\displaystyle \cosh u={\frac {e^{u}+e^{-u}}{2}}}

sinh ⁡ ⁡ --> u = e u − − --> e − − --> u 2 {\displaystyle \sinh u={\frac {e^{u}-e^{-u}}{2}}}

单位双曲线中双曲线扇形的面积是对应直角双曲线 x y = 1 {\displaystyle xy=1} 下双曲角的 1/2。

虚数圆角定义

双曲角经常定义得如同虚数圆角。实际上，如果 x 是实数而i = −1，则

所以双曲函数cosh和sinh可以通过圆函数来定义。这些恒等式不是从圆或旋转得来的，它们应当以无穷级数的方式来理解。特别是，可以将指数函数表达为由偶次项和奇次项组成，前者形成cosh函数，后者形成了sinh函数。cos函数的无穷级数可从cosh得出，通过把它变为交错级数，而sin函数可来自将sinh变为交错级数。上面的恒等式使用虚数i，从三角函数的级数的项中去掉交错因子(−1) ，来恢复为指数函数的那两部分级数。

双曲函数可以通过虚数圆角定义为：

这些复数形式的定义得出自欧拉公式。

与三角函数的类比

奥古斯都·德·摩根在其1849年出版的教科书《Trigonometry and Double Algebra》中将圆三角学扩展到了双曲线 。威廉·金顿·克利福德在1878年使用双曲角来参数化单位双曲线。

给定相同的角α，在双曲线上计算双曲角的量值（双曲扇形面积除以半径）得到双曲函数，角α得到三角函数。在单位圆和单位双曲线上，双曲函数与三角函数有如下的关系:

正弦同样是从x轴到曲线的半弦。

余弦同样是从y轴到曲线的半弦（图中的余弦是长方形的另一条边）。

正切同样是过x轴上单位点（1,0）在曲线上的切线到终边的长度。

余切同样是从y轴与过终边和曲线交点的切线与y轴的交点和曲线连线之长度。

正割同样是在一个有正切和单位长的直角三角形上，但边不一样。

余割同样是y轴与过终边和曲线交点的切线与y轴的交点和原点之距离。

角的量值可以从0到无限大，但α实际上只会介于0到 2 π π --> {\displaystyle 2\pi } （360度）之间，其余是α的同界角，再绕着圆旋转，故三角函数可以有周期。双曲角的量值可以从0到无限大，但α实际上不会超过 π π --> 4 {\displaystyle {\frac {\pi }{4}}} （45度），故无法如三角函数一样有周期性。

恒等式

与双曲函数有关的恒等式如下:

加法公式：

二倍角公式：

半角公式：

由于双曲函数和三角函数之间的对应关系，双曲函数的恒等式和三角函数的恒等式之间也是一一对应的。对于一个已知的三角函数公式，只需要将其中的三角函数转成相应的双曲函数，并将含有有两个sinh的积的项（包括 coth 2 ⁡ ⁡ --> x , tanh 2 ⁡ ⁡ --> x , csch 2 ⁡ ⁡ --> x , sinh ⁡ ⁡ --> x sinh ⁡ ⁡ --> y {\displaystyle \coth ^{2}x,\tanh ^{2}x,\operatorname {csch} ^{2}x,\sinh x\sinh y} ）转换正负号，就可得到相应的双曲函数恒等式 。如

三倍角公式：

差角公式：

双曲函数的导数

双曲函数的泰勒展开式

双曲函数也可以以泰勒级数展开:

其中

双曲函数的积分

与指数函数的关系

从双曲正弦和余弦的定义，可以得出如下恒等式:

和

复数的双曲函数

因为指数函数可以定义为任何复数参数，也可以扩展双曲函数的定义为复数参数。函数sinh z 和cosh z 是全纯函数。

指数函数与三角函数的关系由欧拉公式给出：

所以:

因此，双曲函数是关于虚部有周期的，周期为 2 π π --> i {\displaystyle 2\pi i} (对双曲正切和余切是 π π --> i {\displaystyle \pi i} ).

反双曲函数

反双曲函数 是双曲函数的反函数。它们的定义为：

参见

反双曲函数

双曲函数符号

三角函数

古德曼函数

外部链接

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。