“方程”一词的来历

方程一词出现在中国早期的数学专著《九章算术》中 ，其“卷第八”即名“方程”。卷第八（一）为：

翻成白话即为：

现在这里有上等黍3捆、中等黍2捆、下等黍1捆，打出的黍共有39斗；有上等黍2捆、中等黍3捆、下等黍1捆，打出的黍共有34斗；有上等黍1捆、中等黍2捆、下等黍3捆，打出的黍共有26斗。问1捆上等黍、1捆中等黍、1捆下等黍各能打出多少斗黍？

其“方程术”用阿拉伯数字表示即为：

1 2 3 2 3 2 3 1 1 26 34 39 {\displaystyle {\begin{array}{*{20}c}1&2&3\\2&3&2\\3&1&1\\{26}&{34}&{39}\\\end{array}}}

《九章算术》采用直除法即以一行首项系数乘另一行再对减消元来解方程。

若设可打出黍的斗数分别为1捆上等黍 x {\displaystyle x\,} 斗、1捆中等黍 y {\displaystyle y\,} 斗、1捆下等黍 z {\displaystyle z\,} 斗，可列方程组如下：

{ 3 x + 2 y + z = 39 , 2 x + 3 y + z = 34 , x + 2 y + 3 z = 26. {\displaystyle \left\{{\begin{array}{l}3x+2y+z=39,\\2x+3y+z=34,\\x+2y+3z=26.\\\end{array}}\right.} 解得 { x = 9 1 4 , y = 4 1 4 , z = 2 3 4 . {\displaystyle \left\{{\begin{array}{l}x=9{\frac {1}{4}},\\y=4{\frac {1}{4}},\\z=2{\frac {3}{4}}.\\\end{array}}\right.}

由此可知，此时的“方程”指的是包含多个未知量的联立一次方程组，即现在的线性方程组。

到了魏晋时期，大数学家刘徽注《九章算术》时，给这种“方程”下的定义是：

这里所谓的“课程”指的是按不同物品的数量关系列出的式子。“实”就是式中的常数项。“令每行为率”，就是由一个条件列一行式子，横列代表一个未知量。“如物数程之”，就是有几个未知数就必须列出几个等式。“方”的本义是并，将两条船并起来，船头拴在一起，谓之方。故而列出的一系列式子称“方程”。

已知数及未知数

方程常用来表示一些已知的量和未知的量之间的关系，前者称为已知数，后者称为未知数。一般表示未知数的符号会用英文字母最后的几个，如 x , y , z , w ,…等，而已知数若以符号表示时，会用英文字母前面的几个，如 a , b , c , d ,…等。将未知数用已知数来表示的过程称为解方程。若方程只有一个未知数，使方程成立的未知数数值称为方程的根或是解。方程组是由几个方程所组成，其中也有数个未知数，此时方程的解是一组未知数的值，使得所有方程均成立。

若方程的解可以由有限次常见运算的组合，这种解称为解析解，较复杂的方程不一定可以找出解析解，或解析解根本不存在，但仍可以利用数值分析的方式解方程，此时得到的解称为数值解。

用天平来类比方程

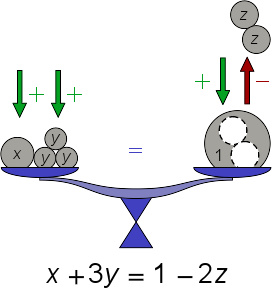
  用图像来类比方程，其中 x , y , z 为实数，用砝码来类比

天平或翘翘板可以用来类比方程。

天平的两边对应方程等号的两侧，可以放不同的表示式数值。若天平两侧平衡，表示等号两侧的数值相等。若天平两侧不平衡，此情形可以用不等式表示。

在图示中， x ， y 和 z 都表示不同的量（例如实数），方程两侧同加一数对应在天平两侧加等重重物，同减一数对应在天平两侧移去等重重物，只要等式成立，就表示二侧的数值相等。

方程组

方程组也称为联合方程，是指两个或两个以上的方程，一般也会有多个未知数。方程组的解是指一组未知数的值可以使这几个方程同时成立。例如以下的系统

有唯一解 x = −1, y = 1。

方程的种类

方程可以依其中用到的运算及未知数的条件加以分类，以下是一些重要的种类：

代数方程是指只由已知数及未知数的代数运算组合的方程，包括整式方程、分式方程与根式方程。

整式方程与分式方程统称“有理方程”。

根式方程也称作“无理方程”，是指方程被开方式中至少含有一个未知数，而根指数不含未知数的方程。

有理方程与无理方程统称“代数方程”。

超越方程是指包含超越函数的方程 ，也叫做“非代数方程”。

函数方程是指其中包含未知函数的方程。

不定方程是其中未知数不只一组的方程。

差分方程是其中未知数为一数列的方程。

整式方程

整式方程为等式两边均为多项式的方程，若以p表示多项式，则以下的方程即为整式方程：

多项式p的零点即为代数方程的解，整式方程还可以依多项式的次数细分为一次方程、二次方程等。四次方程及次数较低的一元整式方程，其所有根都可以用多项式系数的有限次的四则运算及开方来表示。为了解决高次方程的根能否用上述方式表示，引进伽罗瓦理论，也证明五次方程及更高次的方程无法用公式求解，这也是19世纪代数学的重大发现。

数学史上许多重大的发现都和一元整式方程有关，例如边长为1的正方数，其对角线为无理数 2 {\displaystyle {\sqrt {2}}} ，也就是二次方程 x 2 = 2 {\displaystyle x^{2}=2} 的解。而在三次方程 x 3 + p x + q = 0 {\displaystyle x^{3}+px+q=0} 的一个解可用以下公式求得

三次方程的计算过程中有时需要为负数开平方，因此需导入复数的概念及相关计算 。

函数方程

函数方程是指未知量为一函数的方程。常见的是方程现函数导数的微分方程，微分方程在物理学中有许多的应用，微分方程又可以分为常微分方程及偏微分方程。

离散系统下的差分方程可以对应连续系统的微分方程。在数值分析中也会用差分方程来近似微分方程的解。

函数方程解的种类

微分方程及差分方程的解，可以分为一般解（general solution）及奇解（singular solution）二种：

例如以下的克莱罗方程

其一般解为

而其奇解为

不定方程和丢番图方程

不定方程是不止有一个解的方程或方程组，例如2x = y有无限多组解，就是一种简单的不定方程。

若不定方程中有多个未知数，有时其解可以用参数方程来表示。例如上式的解可以表示为以下的 参数方程：

丢番图方程属于不定方程，是变数仅容许是整数的整数系数多项式等式；即形式如 a 1 x 1 b 1 + a 2 x 2 b 2 + . . . . . . + a n x n b n = c {\displaystyle a_{1}x_{1}^{b_{1}}+a_{2}x_{2}^{b_{2}}+......+a_{n}x_{n}^{b_{n}}=c} 的等式，并且其中所有的 a j {\displaystyle a_{j}} 、 b j {\displaystyle b_{j}} 和 c {\displaystyle c} 均是整数，若其中能找到一组整数解 m 1 , m 2 . . . m n {\displaystyle m_{1},m_{2}...m_{n}} 者则称之有整数解。

丢番图问题一般可以有数条等式，其数目比未知数的数目少；丢番图问题要求找出对所有等式都成立的整数组合。用另一种语言来说，丢番图问题定义代数曲线或者代数曲面，或更为一般的几何形，要求找出其中的栅格点。对丢番图问题的数学研究称为 丢番图分析 。线性丢番图方程为线性整数系数多项式等式，即此多项式为次数为0或1的单项式的和。

丢番图方程的名字来源于3世纪希腊数学家亚历山大城的丢番图 ，他曾对这些方程进行研究，并且是第一个将符号引入代数的数学家。

关于丢番图方程的理论的形成和发展是二十世纪数学一个很重要的发展。丢番图方程的例子有贝祖等式、勾股定理的整数解、四平方和定理和费马最后定理等。

性质

对一方程进行以下的处理，处理后的方程和原方程会有相同的解：

在等式二边加任意的实数。

在等式二边减任意的实数。

在等式二边乘任意不为零的实数。

在等式二边除任意不为零的实数。

可以将等式二边套用函数，等式二边需使用相同的函数，而且需确认套用函数后不会造成方程增根或减根的情形。例如方程 y x = x {\displaystyle yx=x} 有二个解： y = 1 {\displaystyle y=1} （x为任意值）及 x = 0 {\displaystyle x=0} （y为任意值）。等式二边平方，方程变成 ( x y ) 2 = x 2 {\displaystyle (xy)^{2}=x^{2}} ，新的方程除了原来的解外，还多了一个解 y = − − --> 1 {\displaystyle y=-1} （x为任意值）。

上述的性质1至4，表示在抽象代数中，方程是体的一种同余关系。

最常见可进行上述运算的数体是实数，不过若方程的数体是自然数，则不能进行减法及除法的运算，因为会产生负数或非整数等不是自然数的数。若方程的数体是整数，则不能进行除法的运算，但可以进行减法的运算。

若一不是单射函数的函数套用在等式二边，原方程的解也是新方程的解，但新方程的解会比原方程多（即增根），新方程的用处较少，上述性质1、2和4是单射函数，性质3在不乘以0时也符合单射函数的条件，一些广义的乘积（如内积）就不是单射函数。

上述性质可以用在代数方程的求解。

参见

表示式

方程组

微分方程

函数方程

参数方程

方程理论

公式编辑器

不等式

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。