概论

微分形式

一般的连续性方程，其微分形式为

其中，φ φ -->{\displaystyle \varphi } 是某物理量 q{\displaystyle q} 的密度（物理量每单位体积），f{\displaystyle \mathbf {f} } 是 q{\displaystyle q} 的流量密度（物理量每单位面积每单位时间）的矢量函数（vector function），s{\displaystyle s} 是 q{\displaystyle q} 的生成量每单位体积每单位时间。

假若 s>0{\displaystyle s>0} 则称 s{\displaystyle s} 为“源点”；假若 s<0{\displaystyle s{\displaystyle \varphi } 是守恒量，不能够生成或湮灭（例如，电荷），则 s=0{\displaystyle s=0} ，连续性方程变为

从简单的“能量连续性方程”到复杂的纳维-斯托克斯方程，这方程可以用来表示任意连续性方程。这方程也是平流方程（advection equation）的推广。

其它物理学里的方程，像电场的高斯定律或高斯引力定律（Gauss" law for gravity），都具有类似连续性方程的数学形式，但是通常不会称为连续性方程，因为 f{\displaystyle \mathbf {f} } 并不代表真实物理量的流动。

积分形式

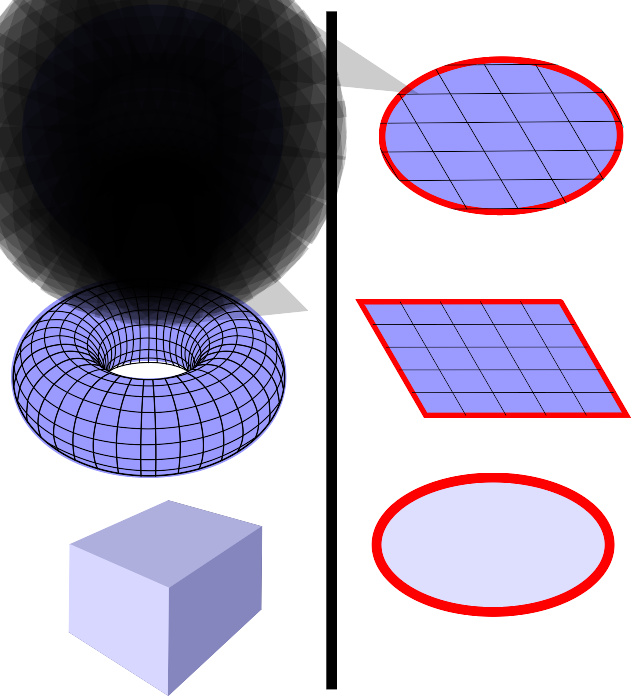
在连续性方程的积分形式里，S{\displaystyle \mathbb {S} } 是包住体积 V{\displaystyle \mathbb {V} } 的任意闭曲面。如同图内左边的曲面（以蓝色显示），S{\displaystyle \mathbb {S} } 没有边界；而图内右边的曲面都有边界（以红色显示）。

根据散度定理，连续性方程可以写为等价的积分形式：

其中，S{\displaystyle \mathbb {S} } 是包住体积 V{\displaystyle \mathbb {V} } 的任意固定（不随时间改变）闭曲面，Q{\displaystyle Q} 是在体积 V{\displaystyle \mathbb {V} } 内的 q{\displaystyle q} 总量，S=∫ ∫ -->Vs d3r{\displaystyle S=\int _{\mathbb {V} }s\ \mathrm {d} ^{3}r} 是在积分体积 V{\displaystyle \mathbb {V} } 内源点与汇点的总生成量每单位时间，da{\displaystyle \mathrm {d} \mathbf {a} } 是微小面矢量积分元素。

举一简例，假设 V{\displaystyle \mathbb {V} } 是台北101大楼，Q{\displaystyle Q} 是在大楼内某时间的总人数，S{\displaystyle \mathbb {S} } 是由门口、墙壁、屋顶、地基等等，共同组成的曲面，则连续性方程表明，当人们进入大楼时（代表穿过曲面的内向通量），或当大楼里面的孕妇生产时（代表源点的 s>0{\displaystyle s>0} ），在大楼里面的总人数会增加；而当人们离开大楼时（代表穿过曲面的外向通量），在大楼里面的总人数会减少。

电磁理论

在电磁理论里，连续性方程可以视为一条经验定律，表达定域电荷守恒，或是从麦克斯韦方程组推导出的结果。“电荷连续性方程”表明，电荷密度ρ ρ -->{\displaystyle \rho } 的变率与电流密度J{\displaystyle \mathbf {J} } 的散度，两者的代数和等于零：

导引

麦克斯韦-安培方程为

其中，B{\displaystyle \mathbf {B} } 是磁场，E{\displaystyle \mathbf {E} } 是电场，μ μ -->0{\displaystyle \mu _{0}} 是磁常数，ϵ ϵ -->0{\displaystyle \epsilon _{0}} 是电常数。

取散度于方程的两边，由于旋度的散度必是零，

高斯定律的方程为

将这方程代入，可以得到

电流是电荷的流量。连续性方程可以这样论述：假若电荷从某微小体积元素移动出去（电流密度的散度是正值），则在那微小体积元素内的总电荷量会减少，电荷密度的变率是负值。从这解释可以察觉，连续性方程就是电荷守恒。

四维电流

四维电流密度定义为

其中，α α -->{\displaystyle \alpha } 标记哪一个时空坐标，c{\displaystyle c} 是光速。

电荷守恒可以简洁地表达为四维电流密度的散度，即连续性方程

其中，∂ ∂ -->α α --> =def (∂ ∂ -->∂ ∂ -->r0,∂ ∂ -->∂ ∂ -->r1,∂ ∂ -->∂ ∂ -->r2,∂ ∂ -->∂ ∂ -->r3)=(∂ ∂ -->c∂ ∂ -->t,∂ ∂ -->∂ ∂ -->x,∂ ∂ -->∂ ∂ -->y,∂ ∂ -->∂ ∂ -->z){\displaystyle \partial _{\alpha }\ {\stackrel {def}{=}}\ ({\frac {\partial }{\partial r^{0}}},{\frac {\partial }{\partial r^{1}}},{\frac {\partial }{\partial r^{2}}},{\frac {\partial }{\partial r^{3}}})=({\frac {\partial }{c\partial t}},{\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}})} 。

流体力学

在流体力学里，连续性方程表明，在任何稳定态过程中，质量进入物理系统的速率等于离开的速率。。连续性方程类比于电路学的基尔霍夫电流定律。“质量连续性方程”的微分形式为

其中，ρ ρ -->{\displaystyle \rho } 是流体质量密度，u{\displaystyle \mathbf {u} } 是流速矢量场，两者相乘后为质量通量。

假设流体是不可压缩流，则密度 ρ ρ -->{\displaystyle \rho } 是常数，质量连续性方程简化为体积连续性方程：

这意味着，在所有位置，速度场的散度等于零；也就是说，定域的体积变率为零。

在另一方面，纳维-斯托克斯方程是一个矢量连续性方程，描述动量守恒。

能量

根据能量守恒，能量只能够传输，不能够生成或湮灭，这导致“能量连续性方程”。这是在热力学定律（Laws of thermodynamics）外，又一种关于能量守恒的数学论述。以方程表达，

其中，u{\displaystyle u} 是能量密度（能量每单位体积），q{\displaystyle q} 是能量通量矢量（数值大小为传输的能量每单位截面面积每单位时间，方向为截面的法向方向）。

根据傅里叶定律（Fourier"s law），对于均匀传导介质，

其中，k{\displaystyle k} 是热导率，T{\displaystyle T} 是温度函数。

能量连续性方程又可写为

量子力学

在量子力学里，从概率守恒可以得到“概率连续性方程”。设定一个量子系统的波函数为 Ψ Ψ -->(x,t){\displaystyle \Psi (x,t)} 。定义概率流 J{\displaystyle \mathbf {J} } 为

其中，ℏ ℏ -->{\displaystyle \hbar } 是约化普朗克常数，m{\displaystyle m} 是质量，Ψ Ψ -->∗ ∗ -->{\displaystyle \Psi ^{*}} 是 Ψ Ψ -->{\displayst共轭复数\Psi } 是共轭复数，Im(){\displaystyle {\mbox{Im}}()} 是取括弧内项目的复值。

连续方程与概率保守定律

概率流满足量子力学的连续方程：

其中，ρ ρ -->=|Ψ Ψ -->|2{\displaystyle \rho =|\Psi |^{2}} 是概率密度。

应用高斯公式，等价地以积分方程表示，

其中，V{\displaystyle \mathbb {V} } 是任意三维区域，S{\displaystyle \mathbb {S} } 是 V{\displaystyle \mathbb {V} } 的边界曲面。

这就是量子力学概率守恒定律的方程。

方程 (1) 左边第一个体积积分项目（不包括对于时间的偏微分），即是测量粒子位置时，粒子在 V{\displaystyle \mathbb {V} } 内的概率。第二个曲面积分是概率流出 V{\displaystyle \mathbb {V} } 的通量。总之，方程 (1) 表明，粒子在三维区域 V{\displaystyle \mathbb {V} } 内的概率对于时间的微分，加上概率流出三维区域 V{\displaystyle \mathbb {V} } 的通量，两者的总和等于零。

连续方程导引

测量粒子在三维区域 V{\displaystyle \mathbb {V} } 内的概率 P{\displaystyle P} 是

概率对于时间的导数是

假设 Ψ Ψ -->{\displaystyle \Psi } 的含时薛定谔方程为

其中，U(r){\displaystyle U(\mathbf {r} )} 是位势。

将含时薛定谔方程代入方程 (2) ，可以得到

应用一则矢量恒等式，可以得到

这方程右手边第一个项目与第三个项目互相抵销，将抵销后的方程代入，

将概率密度方程与概率流定义式代入，

这相等式对于任意三维区域 V{\displaystyle \mathbb {V} } 都成立，所以，被积项目在任何位置都必须等于零：

参阅

欧拉方程

诺特定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。