性质

面的图形：等边三角形 顶点数目：4 边数目：6 面数目：4 二面角角度： arccos ⁡ ⁡ --> ( 1 3 ) = arctan ⁡ ⁡ --> ( 2 2 ) {\displaystyle \arccos \left({1 \over 3}\right)=\arctan(2{\sqrt {2}})\,} ≈ 70.5288° 面棱夹角： arccos ⁡ ⁡ --> ( 1 3 ) = arctan ⁡ ⁡ --> ( 2 ) {\displaystyle \arccos \left({1 \over {\sqrt {3}}}\right)=\arctan({\sqrt {2}})\,} ≈ 54.7356° 中心-顶点连线之间夹角： arccos ⁡ ⁡ --> ( − − --> 1 3 ) = 2 arctan ⁡ ⁡ --> ( 2 ) {\displaystyle \arccos \left({-1 \over 3}\right)=2\arctan({\sqrt {2}})立体角 ≈ 109.4712° 面所对立体角： arccos ⁡ ⁡ --> ( 23 27 ) {\displaystyle \arccos \left({23 \over 27}\right)} ≈ 0.55129sr对于棱长为a的正四面体： 底面积： A 0 = 3 4 a 2 {\displaystyle A_{0}={{\sqrt {3}} \over 4}a^{2}\,} 高： H = 6 3 a = 2 3 a {\displaystyle H={{\sqrt {6}} \over 3}a={\sqrt {2 \over 3}}\,a\,} 表面积： S = 4 A 0 = 3 a 2 {\displaystyle S=4A_{0}={\sqrt {3}}a^{2}} 体积： V = 1 12 2 a 3 {\displaystyle V={1 \over 12}{\sqrt {2}}a^{3}} 外接球半径： 6 4 a {\displaystyle {\frac {\sqrt {6}}{4}}a} 内切球半径： 6 12 a {\displaystyle {\frac {\sqrt {6}}{12}}a} 中交球半径： r M = r R = 2 a 4 {\displaystyle r_{M}={\sqrt {rR}}={{\sqrt {2}}a \over 4}\,} 旁切球半径： r E = 6 a 6 {\displaystyle r_{E}={{\sqrt {6}}a \over 6}\,} 旁切球到顶点距离： d V E = 6 2 a = 3 2 a {\displaystyle d_{VE}={{\sqrt {6}} \over 2}a={\sqr多面体3 \over 2}}\,a\,} 对偶多面体：正四面体 注意到相对于底面，面的斜率（2√2）是棱的斜率（√2）的两倍，这意味着由于从底面沿棱到顶点的水平距离是沿侧面中线到顶点水平距离的2倍，而这是由于从底面重心到底面顶点的距离是到底面边距离的2倍，这由中心分中线为2:1或是30°直角三角形的三边关系即刻可得出。

坐标系

如果我们以正四面体的中心作为原点建立三维直角坐标系的话，棱长a=2的正四面体的顶点坐标可以表示为：

另一种表示方法把正四面体看作是半立方体，它有立方体一半的顶点：（如果原正方体棱长为1的话，正四面体棱长为√2） (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1) 另外，被交错舍弃掉的那四个顶点构成了与原来正四面体对偶的另一个正四面体： (-1,-1,-1), (-1,1,1), (1,-1,1), (1,1,-1) 它们一起构成了星形八面体。

正交投影

正四面体有2个特殊角度的正交投影，即一下列表中的两个。第一个投影对应着正四面体的A 3 考克斯特平面 （ 英语 ： Coxeter plane ） 。

具有其它对称形式的正四面体

正四面体是所有四面体中对称性最高的，而然它也可被看作是更低对称性四面体的特殊形式，例如正四面体是特殊的复正方锲形体，这种四面体拥有4个全等的等腰三角形（对于正四面体，这些等腰三角形的底和腰相等了，成为了等边三角形），可以被描述为正四棱柱的交错（对于正四面体，这个正四棱柱是正方形），一种能够密铺空间的四面体就是复正方锲形体。另外还有复斜方锲形体和二面体锲形体，它们分别是长方体和任意四角六面体的交错。

此外，由于正四面体具有高度的对称性，它还是其它一些四面体的特例，例如： 垂心四面体 （ 英语 ： Orthocentric tetrahedron ） ，因为其3组相对的边互相垂直；等力四面体，因为其所有4条顶点到对面内心连线（一种 塞瓦线 （ 英语 ： Cevian ） ）是共点的；等角四面体，因为其所有顶点到对面与内切球切点的连线是共点的。

等距同构下的对称性

正四面体等距同构对称变换群

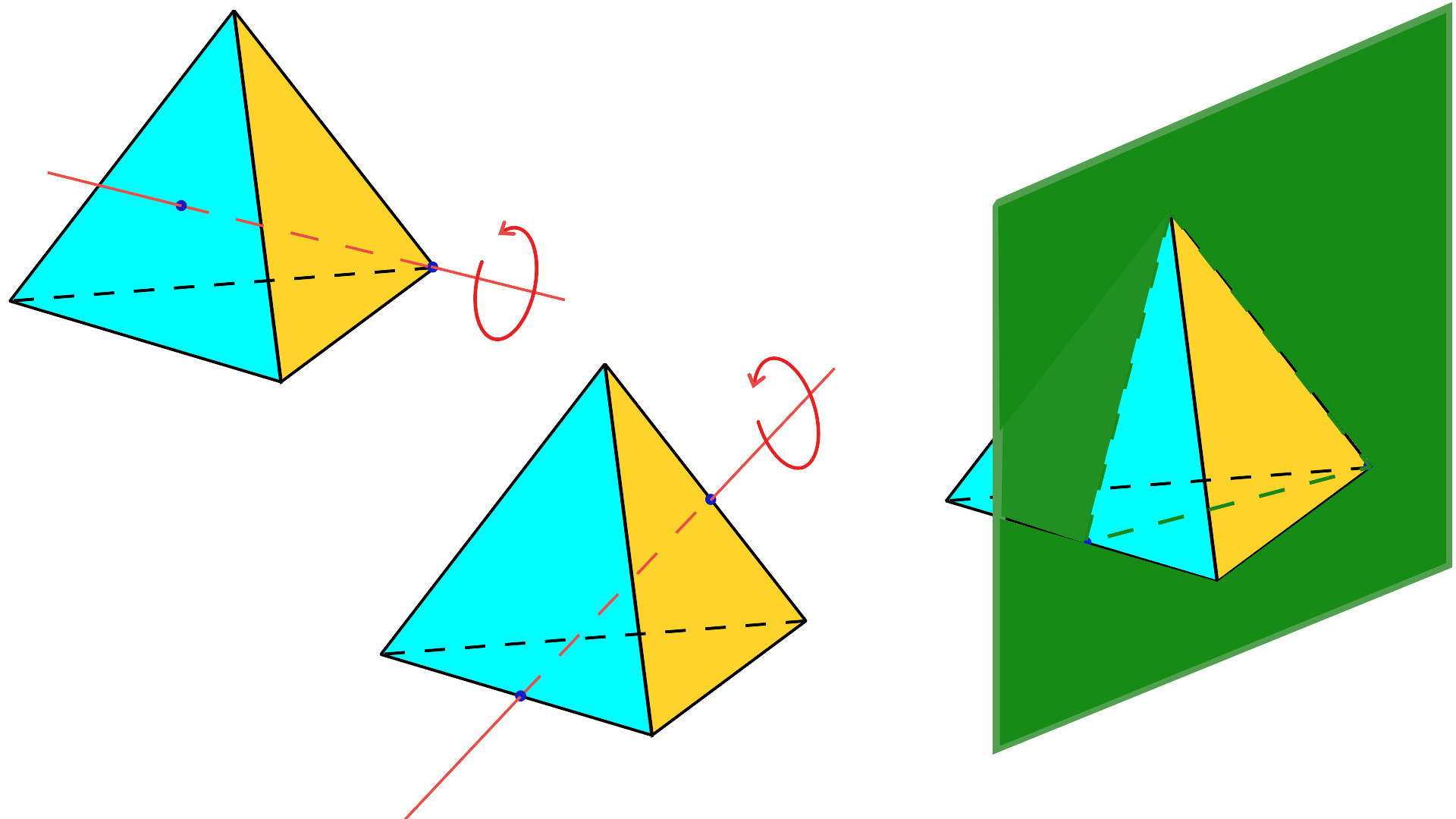
严格旋转—顶点对面120°（3阶）旋转、边对边180°（2阶）旋转；及镜面对称（沿一条边、穿过两面即一边）

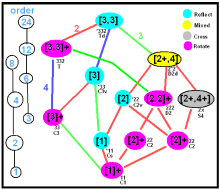
正四面体子对称群之间的关系

立方体的8个顶点可以交错着被分成2组，每一组都能组成一个正四面体，这意味着正四面体拥有立方体一半的对称性，即那些能将立方体内部的正四面体变换到自身而不是对方的对称性。而由于立方体的所有中心对称都会将内接正四面体变换到对方，因此正四面体是柏拉图立体中唯一一个没有中心对称性的。 正四面体有24个不同的等距同构的对称变换，形成了对称群 T d ，[3,3]，(*332)，与对称群 S 4 同构。它可以用如下方式分类：

T ，[3,3]+，(332)，与交错群 A 4 （包括单位元和11个严格旋转）同构，再加上下述共轭类。（在括号内给出的是顶点排列，或者说是相对应的面和单位四元数表示。）

关于垂直于边的平面的镜面对称：6个。

关于平面的镜面对称加上关于垂直于该平面的直线的90°旋转的混合。三条轴，每条轴对应2个旋转，共6个。另外，还有90°旋转加上中心对称变换，旋转轴对应着立方体的面对面旋转轴。

正四面体的非正四面体子对称变换群

7种非正四面体（无标记）的对称性取决于它的几何特征。任何一种非正对称变换组都能组成一个三维点群，另外两种对称性（ C 3 , [3] ）和( S 4 , [2 ,4 ])要求面和棱标记是被允许的。

几何关联

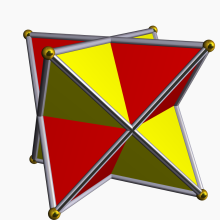
星形八面体

复锲形体堆砌

正四面体是三维的单纯形，这个家族在所有维度的成员都是凸的多面体。它们都具有类似的几何性质，比如它们n维元素都符合一个相同的规律（杨辉三角形），以及它们都是该维最简单的多胞形（这也是单纯形英文“simplex”—“简单的复杂”的来源）。

正四面体是一种特殊的正三棱锥，正四面体是自身对偶的。

正四面体可以以两种中心对称的方式内含于立方体，使得正四面体的顶点交错着与立方体顶点重和，而正四面体的棱成为立方体6个面的对角线，对应坐标已在上部分给出。这意味着正四面体就是三维的半立方体。这两个正四面体的任意一个都占据了立方体体积的 / 3 。这样得到的两个正四面体是以互相对偶的方式部分重合的其顶点占据了立方体所有的顶点，它们一起组成了正复合多面体星形八面体，也叫做二复合正四面体，这星形八面体应此是立方体的第一个也是唯一一个 小面化 （ 英语 ： faceting ） （Faceting），而星形八面体两正四面体的交集是正八面体，应此它也是正八面体唯一的 星形化 （ 英语 ： stellation ） （Stellation）。

从这里我们还可以看出来，正八面体是正四面体从各边中点处截下4个包括原顶点在内的线性大小为原正四面体一半的正四面体得到的结果。（这种操作叫“截半”，得到的正八面体是作为“截半四面体”出现的，只具有正四面体的对称性）

从立方体得到正四面体的操作叫“交错”，这种操作将正方体分成5个四面体，其中一个是正的，另外4个是有一个正方体立体角（即从一个顶点发出的3条棱互相正交）的 直角四面体 （ 英语 ： trirectangular tetrahedron ） 。

事实上，我们至少需要5个四面体来堆积一个正方体。

利用内接于五复合立方体中立方体的正四面体，我们还可以构造出另外两个基于正四面体的正复合多面体—五复合正四面体（每个立方体只利用一个）和十复合正四面体（每个立方体利用两个）。考虑到五复合立方体中立方体都是内接与正十二面体的，这两种复合多面体中的正四面体实际上是正十二面体内接的正四面体。事实上，正十二面体的对偶——正二十面体可以被看作是半正的扭棱正四面体，拥有正四面体部分对称性。 正四面体是不能独立密铺三维欧氏空间的，尽管它看上去可能以至于亚里士多德声称它的确是可能的。但是，我们可以将一个正四面体面对面粘到正八面体上得到一个能独立密铺空间的菱面体，或者我们可以直接利用正四面体和正八面体两种多面体去完成一个半正堆砌，即 正四面体—正八面体堆砌 （ 英语 ： demcubic honeycomb ） 。但是，一些非正的四面体却可以胜任，比如 复锲形体堆砌 （ 英语 ： Disphenoid tetrahedral honeycomb ） ，完整的列表还有待研究。如果我们不要求参与堆砌的正四面体都是全等的话，可能性会更丰富一些。比如说。我们可以将正八面体沿一条对角线劈开分成4个全等的锲形体，然后再拿两个正的与它们堆砌。（事实上这样做后锲形体与正四面体体积相等）。 正四面体是柏拉图立体中唯一一个不存在互相平行的面的。

相关多面体

正四面体是特殊的棱锥，所以它与其它棱锥相关联：

正四面体属于正四面体家族（该家族都具有相同的或更高的对称性）。这些与正四面体相关的半正多面体都是通过3种不同的截形操作（截顶、截棱、截半）和交错，及其组合构造出来的，其中截半正四面体（正八面体）和全截正四面体（截顶正八面体）拥有更高的正八面体对称性，而扭棱正四面体（正二十面体）拥有更高的正二十面体对称性。正四面体的二次截半将其面截成了顶点，使其成为与原来对偶的正四面体。

正四面体在拓扑上关联与一组一直延伸到双曲镶嵌的正三角形镶嵌{3,n}。

正四面体在拓扑上关联与一组一直延伸到双曲镶嵌的三阶正镶嵌{3,n}。

与正四面体有关的复合正多面体

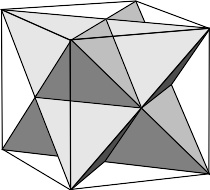
二复合四面体

五复合四面体

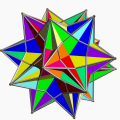
十复合四面体

其中五复合四面体是个有手征性的复合多面体（在折纸艺术中，该复合多面体经常出现）。五复合和十复合四面体都是内接于正十二面体的。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。