开普勒猜想-族谱新闻-族谱网

开普勒猜想

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:1154次

转发:0次

评论:0

背景面心立方（左）与六方最密堆积（右）示意图若将一个容积很大的容器，以大量体积很小且体积彼此相等的小球给填充（显然不可能完全填满，一定会有些空隙留下），那其密度就是指所有小球体积的总和对容器空间的比值。若欲使该容器中能放入尽可能多的小球，就必须寻找密度最高的排列法，也就是使这些被装填的小球彼此间能尽可能紧密地排在一起。有人做过实验，并发现随机装填的密度大约有65%，然而小心地排列球的位置，可达致更高的密度。若在第一层，先将球以六角形的方式排列（即每个球四周围绕六颗球），然后下一层的球放在“于上一层球之上能让球中心位置最低的点”上，然后其余层以此类推。这就是在市场水果摊上橘子堆叠的方式。每个阶段对于下一层该如何摆放，都有着两种选择，故若一直重复此法，到了最后，会有无限多的、密度相同的球的堆叠存在，此法最为人知的两种形式，即是面心立方和六方最密堆积这两种方法（这两种方法的平均密度相同），此法的...

背景

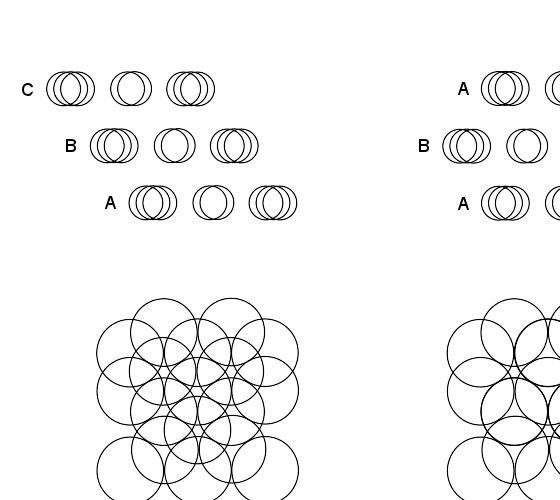
面心立方（左）与六方最密堆积（右）示意图

若将一个容积很大的容器，以大量体积很小且体积彼此相等的小球给填充（显然不可能完全填满，一定会有些空隙留下），那其密度就是指所有小球体积的总和对容器空间的比值。若欲使该容器中能放入尽可能多的小球，就必须寻找密度最高的排列法，也就是使这些被装填的小球彼此间能尽可能紧密地排在一起。

有人做过实验，并发现随机装填的密度大约有65%，然而小心地排列球的位置，可达致更高的密度。若在第一层，先将球以六角形的方式排列（即每个球四周围绕六颗球），然后下一层的球放在“于上一层球之上能让球中心位置最低的点”上，然后其余层以此类推。这就是在市场水果摊上橘子堆叠的方式。每个阶段对于下一层该如何摆放，都有着两种选择，故若一直重复此法，到了最后，会有无限多的、密度相同的球的堆叠存在，此法最为人知的两种形式，即是面心立方和六方最密堆积这两种方法（这两种方法的平均密度相同），此法的平均密度如下：

开普勒猜想说，这是所有可能的装球排列法所能达到的最高密度，没有更高的了。

起源

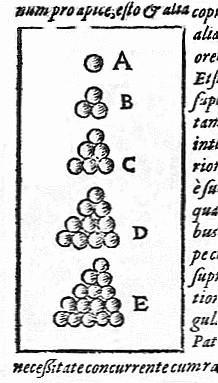
《Strena Seu de Nive Sexangula》这书里的一张图。这图的内容即开普勒猜想

此猜想最早在1611年，由约翰内斯·开普勒在其文章“关于六角雪花”（On the six-cornered snowflake）中提出。他研究了球的排列，并于1606年将之写在与英国数学家兼天文学家托马斯‧哈利欧特（Thomas Harriot）的信中。哈利欧特是华特‧拉雷（Sir Walter Raleigh）的朋友与助手，拉雷给了哈利欧特“在他船支的甲板上该怎样堆叠炮弹才是最好的”这个问题。哈利欧特曾在1591年出版一本关于各种堆叠问题的研究，并曾发展出某种早期的原子论来。

十九世纪的发展

开普勒并未证明他的猜想，而此猜下的下一步发展则由卡尔·弗里德里希·高斯所推展，高斯在1831年证明了若球必须在规则格中进行排列，则开普勒猜想是正确的。

这就表示任何可反证开普勒猜想的球排列方式必然是不规则的排列方式。然而要排除任何可能的不规则排列法是非常困难的，而这也是开普勒猜想之所以如此难以证明的原因。实际上，当装球的空间足够小时，确实是有些不规则排列法的密度是高于面心立方排列法的，但当这些不规则排列法被推广至更大的空间时，其密度总会降低。

在高斯出手后，整个十九世纪就再也没有人在此定理上做出更进一步的推展了。1900年，希尔伯特将此问题包含在希尔伯特的23个问题中，做为希尔伯特第十八问题的一部分。

廿世纪的进展

开普勒猜想的下一步进展，由匈牙利数学家拉斯罗‧费耶斯‧托特（László Fejes Tóth）展开，他在1953年证明了决定任何排列法密度的问题，可变为有限量的计算过程（唯需要的计算量非常大）。这表示至少在原则上，透过穷举法证明此定理是可能的。就如托特所言，一台运算速度足够快的电脑，可使这个理论上的结果，转化为对此问题实际的证明过程。

与此同时，人们也努力地寻找三维空间里任何可能的装球方法的上界。英国数学家在1958年给出了一个78%的上界，之后数学家的努力稍微缩减了此数值，唯此数值距离面心立方密度的数值，也就是上述的74%左右的数值，依旧有一段距离。

项武义在1993年和2001年曾宣称自己借由几何的方法，证明了开普勒猜想。然而嘉伯‧费耶斯‧托特（拉斯罗‧费耶斯‧托特的儿子）却在看此文后，说道：“在考虑细节后，我认为其证明许多关键性的陈述都没有可接受的证明。”

黑尔斯在1994年丢出了对项武义证明较为详尽的批评，项武义则在1995年对此进行回应。现在一般的看法认为项武义的证明是不完善的。

黑尔斯的证明

托马斯·黑尔斯决定根据费耶斯‧托特在1953年提出的思路来证明此猜想，他认为可透过一个有着150个变数的方程式的最小值，来找出任何可能装球排法的最大密度。在1992年，在其研究生山谬尔‧费尔古生（Samuel Ferguson）的帮助下，他开始了一个借由系统化地应用线性规划的方法，对超过五千种不同的装球法的每一个，找出其所提出的方程式的下界的研究。如果此方程式对于这些装球法的下界都超过（此方程式对于）面心立方的值的话，那开普勒猜想就可得证。若要寻找每种情况的下界，则需要解超过十万个线性规划问题。

当托马斯·黑尔斯在1996年公开其计划时，他说这证明的结果近了，然而依旧需要“一两年的时间”来完成它。在1998年，托马斯·黑尔斯宣布他的证明已经完成了。在此阶段，其证明包含了250页的注解与3GB的电脑档案，其中包括了计算机程序、资料和结果等。

虽然这证明在本质上是不寻常的，但因一个由20名裁判员组成的小组接受其内容，《数学年报》（Annals of Mathematics）依旧同意了此论文在其上的发表。2003年，在经过四年的努力后，裁判员小组的头领嘉伯‧费耶斯‧托特报告道他们小组“99%确定了”此证明的正确性，然而他们不能完全确定所有电脑计算的正确性。

托马斯·黑尔斯在2005年出版了一份超过一百页的文档以说明其证明的非电脑部分的细节。费尔古生在2006年及数篇之后发的文则描述了其电脑运作的部分。黑尔斯与费尔古生在2009年，获得了福尔克生奖在离散数学方面杰出论文的奖项（Fulkerson Prize for outstanding papers in the area of discrete mathematics）。

形式证明

在2003年一月，黑尔斯宣布将要开始一个以完成开普勒猜想的形式证明为目标的协作计划。此计划的目标，是要借由产生可由HOL等自动证明检验（Automated proof checking）软件确认其正确性的证明，来移除所有剩余的、和证明有效性相关的不确定成分。这个计划被称作“Project FlysPecK”，其中的F、P和K代表“Formal Proof of Kepler”，也就是“开普勒猜想的形式证明”。黑尔斯认为此计划需要大约20年的时间才能完成。该计划在2014年8月10日宣告完成。在2015年月，黑尔斯和21位协作者共同发表了“开普勒猜想的形式化证明”。