历史

笛卡尔坐标系是由法国数学家勒内·笛卡尔创建的。1637年，笛卡尔发表了巨作《方法论》。这本专门研究与讨论西方治学方法的书，提供了许多正确的见解与良好的建议，对于后来的西方学术发展，有很大的贡献。为了显示新方法的优点与果效，以及对他个人在科学研究方面的帮助，在《方法论》的附录中，他增添了另外一本书《几何》。有关笛卡儿坐标系的研究，就是出现于《几何》这本书内。笛卡儿在坐标系这方面的研究结合了代数与欧几里得几何，对于后来解析几何、微积分、与地图学的建树，具有关键的开导力。

二维坐标系统

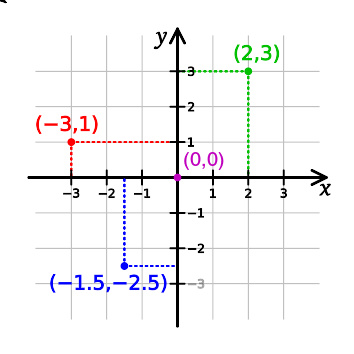
图2 - 直角坐标系。图中四点的坐标分别为，绿点： ( 2 , 3 ) {\displaystyle (2,\ 3)} ，红点： ( − − --> 3 , 1 ) {\displaystyle (-3,\ 1)} ，蓝点： ( − − --> 1.5 , − − --> 2.5 ) {\displaystyle (-1.5,\ -2.5)} ，紫点： ( 0 , 0 ) {\displaystyle (0,\ 0)} 。

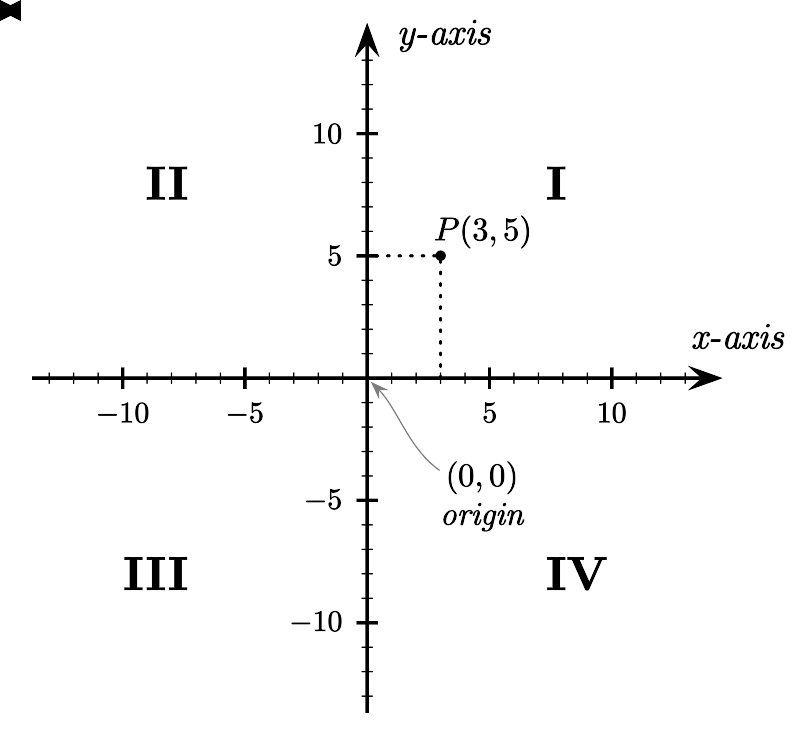
图3 - 直角坐标系的四个象限，按照逆时针方向，从象限 I {\displaystyle I} 到象限 I V {\displaystyle IV} 。坐标轴的头部象征着，往所指的方向，无限的延伸。

参阅图2，二维的直角坐标系通常由两个互相垂直的坐标轴设定，通常分别称为x-轴和 y-轴；两个坐标轴的相交点，称为原点，通常标记为O，既有“零”的意思，又是英语“Origin”的首字母。每一个轴都指向一个特定的方向。这两个不同线的坐标轴，决定了一个平面，称为 xy-平面 ，又称为 笛卡儿平面 。通常两个坐标轴只要互相垂直，其指向何方对于分析问题是没有影响的，但习惯性地（见右图），x-轴被水平摆放，称为横轴，通常指向右方；y-轴被竖直摆放而称为纵轴，通常指向上方。两个坐标轴这样的位置关系，称为二维的右手坐标系，或 右手系 。如果把这个右手系画在一张透明纸片上，则在平面内无论怎样旋转它，所得到的都叫做右手系；但如果把纸片翻转，其背面看到的坐标系则称为“左手系”。这和照镜子时左右对调的性质有关。

为了要知道坐标轴的任何一点，离原点的距离。假设，我们可以刻画数值于坐标轴。那么，从原点开始，往坐标轴所指的方向，每隔一个单位长度，就刻画数值于坐标轴。这数值是刻画的次数，也是离原点的正值整数距离；同样地，背着坐标轴所指的方向，我们也可以刻画出离原点的负值整数距离。称x-轴刻画的数值为 x-坐标 ，又称 横坐标 ，称y-轴刻画的数值为 y-坐标 ，又称 纵坐标 。虽然，在这里，这两个坐标都是整数，对应于坐标轴特定的点。按照比例，我们可以推广至实数坐标和其所对应的坐标轴的每一个点。这两个坐标就是直角坐标系的 直角坐标 ，标记为 ( x , y ) {\displaystyle (x,\ y)} 。

任何一个点P在平面的位置，可以用直角坐标来独特表达。只要从点P画一条垂直于x-轴的直线。从这条直线与x-轴的相交点，可以找到点P的x-坐标。同样地，可以找到点P的y-坐标。这样，我们可以得到点P的直角坐标。例如，参阅图3，点P的直角坐标是 ( 3 , 5 ) {\displaystyle (3,\ 5)} 。

直角坐标系也可以推广至三维空间与高维空间 (higher dimension)。

参阅图3，直角坐标系的两个坐标轴将平面分成了四个部分，称为象限，分别用罗马数字编号为 I ( + , + ) {\displaystyle I\ (+,\ +)} ， I I ( − − --> , + ) {\displaystyle II\ (-,\ +)} ， I I I ( − − --> , − − --> ) {\displaystyle III\ (-,\ -)} ， I V ( + , − − --> ) {\displaystyle IV\ (+,\ -)} 。依照惯例，象限 I {\displaystyle I} 的两个坐标都是正值；象限 I I {\displaystyle II} 的x-坐标是负值，y-坐标是正值；象限 I I I {\displaystyle III} 的两个坐标都是负值的；象限 I V {\displaystyle IV} 的x-坐标是正值，y-坐标是负值。所以，象限的编号是按照逆时针方向，从象限 I {\displaystyle I} 编到象限 I V {\displaystyle IV} 。

三维坐标系统

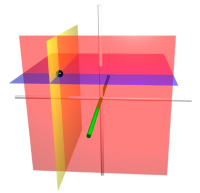
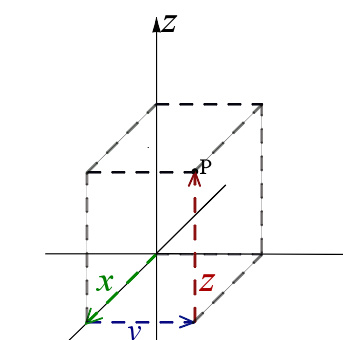
图4 - 直角坐标系的几个坐标曲面。红色平面的 x = 1 {\displaystyle x=1} 。黄色平面的 y = − − --> 1 {\displaystyle y=-1} 。蓝色平面的 z = 1 {\displaystyle z=1} 。z-轴是竖直的，以白色表示。x-轴以绿色表示。三个坐标曲面相交于点P（以黑色的圆球表示），直角坐标大约为 ( 1 , − − --> 1 , 1 ) {\displaystyle (1,\ -1,\ 1)} 。

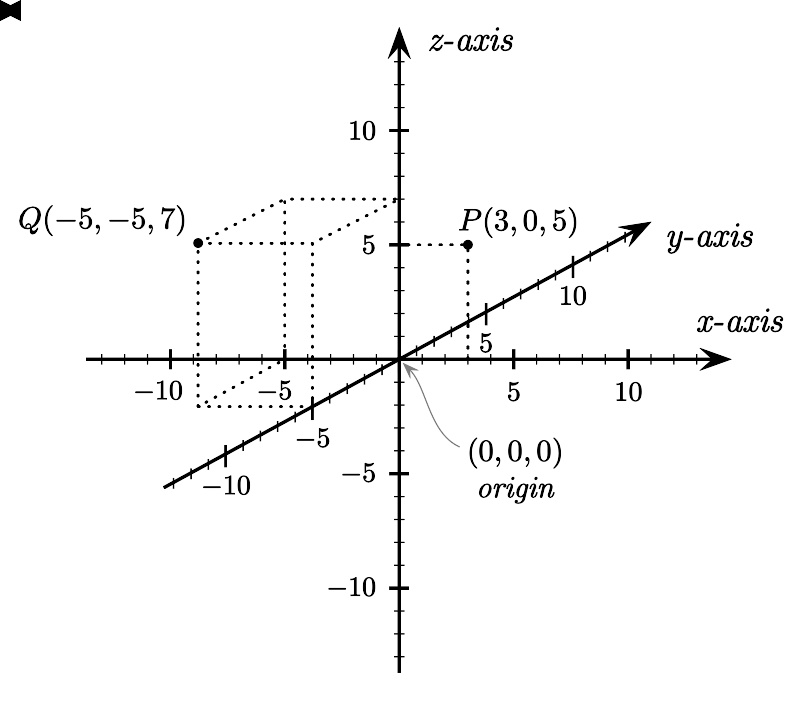
图5 - 三维直角坐标系。y-轴的方向是远离读者。

在原本的二维直角坐标系，再添加一个垂直于x-轴，y-轴的坐标轴，称为 z-轴 。假若，这三个坐标轴满足右手定则，则可得到三维的直角坐标系。这z-轴与x-轴，y-轴相互正交于原点。在三维空间的任何一点P，可以用直角坐标 ( x , y , z ) {\displaystyle (x,\ y,\ z)} 来表达其位置。例如，参阅图5，两个点P与Q的直角坐标分别为 ( 3 , 0 , 5 ) {\displaystyle (3,\ 0,\ 5)} 与 ( − − --> 5 , − − --> 5 , 7 ) {\displaystyle (-5,\ -5,\ 7)} 。

三个平面，xy-平面，yz-平面，xz-平面，将三维空间分成了八个部分，称为卦限(octant)。与二维空间的四个象限不同，只有一个卦限有编号。第一号卦限的每一个点的三个坐标都是正值的。

取向

二维空间

直角坐标系的x-轴与y-轴必须相互垂直。称包含y-轴的直线为y-线。在二维空间里，当我们设定了x-轴的位置与方向的同时，我们也设定了y-线的方向。可是，我们仍旧必须选择，在y-线的以原点为共同点的两条半线中，那一条半线的点的坐标是正值的，那一条是负值的？任何一种选择决定了xy-平面的取向。

参阅图1。通常，我们选择的取向是，正值的x-轴横地指向右方，正值的y-轴纵地指向上方。这种取向称为 正值取向 ， 标准取向 ，或 右手取向 。

右手定则是一种常用的记忆方法，专门用来辨认正值取向：将一只半握拳的右手放在平面上，大拇指往上指，那么，其它的手指都从x-轴指向y-轴。

另外一种取向，采用 左手定则 ，专门用来辨认 负值取向 ，或 左手取向 ：将一只半握拳的左手放在xy-平面上，大拇指往上指，那么，其它的手指都从y-轴指向x-轴。

不论坐标轴是何种取向，将坐标系统做任何角度的旋转，取向仍旧会保持不变。

三维空间

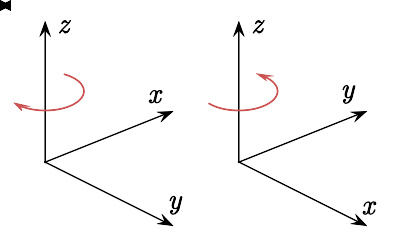
图8 –左边是左手取向，右边是右手取向。

直角坐标系的x-轴，y-轴，与z-轴必须相互垂直。称包含z-轴的直线为z-线。在三维空间里，当我们设定了x-轴，y-轴的位置与方向的同时，我们也设定了z-线的方向。可是，我们仍旧必须选择，在z-线以原点为共同点的两条半线中，哪一条半线的点的坐标是正值的，哪一条是负值的？这两种不同的坐标系统，称为 右手坐标系 与 左手坐标系 。右手坐标系又称为 标准坐标系 ，或 正值坐标系 。

右手坐标系这名词是由右手定则而来的。先将右手的手掌与手指伸直。然后，将中指指向往手掌的掌面半空间，与食指呈直角关系。再将大拇指往上指去，与中指，食指都呈直角关系。则大拇指，食指，与中指分别表示了右手坐标系的x-轴，y-轴，与z-轴。同样地，用左手也可以表示出左手坐标系。

图8试着展示出一个左手坐标系与一个右手坐标系。因为我们用二维画面来展示三维物体，会造成扭曲或模棱两可的图形。指向下方与右方的轴，也有指向读者的意思；而位置居于中间的轴，也有指向读者正在看的方向的意思。平行于xy-平面的红色圆形曲箭，其红色箭头从z-轴前面经过，表示从x-轴往y-轴的旋转方向。

向量

采用直角坐标系，在三维空间里，任何一点P都可以用向量来表示。我们可以想像向量为一支羽箭，其箭尾在原点，箭锋在点P。假若点P的向量是 r {\displaystyle \mathbf {r} } ，直角坐标是 ( x , y , z ) {\displaystyle (x,\ y,\ z)} 。那么，

其中，单位向量 i ^ ^ --> {\displaystyle {\hat {\mathbf {i} }}} ， j ^ ^ --> {\displaystyle {\hat {\mathbf {j} }}} 与 k ^ ^ --> {\displaystyle {\hat {\mathbf {k} }}} 分别指向x-轴，y-轴无穷z-轴指向的正无穷值方向。

参阅

广义坐标

正则坐标

平行坐标

象限角

卦限

正交坐标系

参考文献

Descartes, René. Oscamp, Paul J. (trans). Discourse on Method, Optics, Geometry, and Meteorology . 2001.

参考目录

Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 656. ISBN 978-0-07-043316-8. 引文格式1维护：冗余文本 (link)

Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: p. 177. 引文格式1维护：冗余文本 (link)

Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: pp. 55–79. ASIN B0000CKZX7. 引文格式1维护：冗余文本 (link)

Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 94. 引文格式1维护：冗余文本 (link)

Moon P, Spencer DE. Rectangular Coordinates (x, y, z). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 9–11 (Table 1.01). ISBN 978-0387184302. 引文格式1维护：冗余文本 (link)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。