历史

古希腊数学家梅内克缪斯(Menaechmus)的解题、证明方式与现在使用坐标系十分相似，以至于有时会认为他是解析几何的鼻祖。阿波罗尼奥斯在《论切触》中解题方式在现在被称之为单维解析几何；他使用直线来求得一点与其它点之间的比例。阿波罗尼奥斯在《圆锥曲线论》中进一步发展了这种方式，这种方式与解析几何十分相似，比起笛卡儿早了1800多年。他使用了参照线、直径、切线与现进所使用坐标系没有本质区别，即从切点沿直径所量的距离为横坐标，而与切线平行、并与数轴和曲线向交的线段为纵坐标。他进一步发展了横坐标与纵坐标之间的关系，即两者等同于夸张的曲线。然而，阿波罗尼奥斯的工作接近于解析几何，但它没能完成它，因为他没有将负数纳入系统当中。在此，方程是由曲线来确定的，而曲线不是由方程得出的。坐标、变量、方程不过是一些给定几何题的脚注罢了。

十一世纪波斯帝国数学家欧玛尔·海亚姆发现了几何与代数之间的密切联系，在求三次方程使用了代数和几何，取得了巨大进步。但最关键的一步由笛卡儿完成。

从传统意义上讲，解析几何是由勒内·笛卡儿创立的。笛卡儿的创举被记录在《几何学》(La Geometrie)当中，在1637年与他的《方法论》一道发表。这些努力是以法语写成的，其中的哲学思想为创立无穷小提供了基础。最初，这些著作并没有得到认可，部分原因是由于其中论述的间断，方程的复杂所致。直到1649年，著作被翻译为拉丁语，并被冯·斯霍滕(van Schooten)恭维后，才被大众所认可接受。

费马也为解析几何的发展做出了贡献。他的《平面与立体轨迹引论》(Ad locos planos et solidos isagoge)虽然没有在生前发表，但手稿于1637年在巴黎出现，正好早于笛卡儿《方法论》一点。《引论》文字清晰，获得好评，为解析几何提供了铺垫。费马与笛卡儿方法的不同在于出发点。费马从代数公式开始，然后描述它的几何曲线，而笛卡儿从几何曲线开始，以方程的完结告终。结果，笛卡儿的方法可以处理更复杂的方程，并发展到使用高次多项式来解决问题。

基本理论

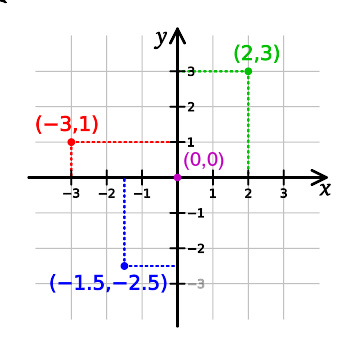
卡氏平面坐标系。四个点被标注了它们的坐标：(2,3)为绿色，(−3,1)为红色，(−1.5,−2.5)为蓝色，原点(0,0)为紫色。

坐标

在解析几何当中，平面给出了坐标系，即每个点都有对应的一对实数坐标。最常见的是笛卡儿坐标系，其中，每个点都有x-坐标对应水平位置，和y-坐标对应垂直位置。这些常写为有序对(x, y)。这种系统也可以被用在三维几何当中，空间中的每个点都以多元组呈现(x, y, z)。

坐标系也以其它形式出现。在平面中最常见的另类坐标系是极坐标系，其中每个点都以从原点出发的半径r和角度θ表示。在三维空间中，最常见的另类坐标系统是圆柱坐标系和球坐标系。

曲线方程

在解析几何当中，任何方程都包含确定面的子集，即方程的解集。例如，方程 y = x 在平面上对应的是所有 x-坐标等于 y-坐标的解集。这些点汇集成为一条直线，y = x 被称为这道方程的直线。总而言之，线性方程中 x 和 y 定义线，一元二次方程定义圆锥曲线，更复杂的方程则阐述更复杂的形象。

通常，一个简单的方程对应平面上的一条曲线。但这不一定如此：方程 x = x 对应整个平面，方程 x + y = 0 只对应(0, 0)一点。在三维空间中，一个方程通常对应一个曲面，而曲线常常代表两个曲面的交集，或一条参数方程。方程 x + y = r 代表了是半径为r且圆心在(0, 0)上的所有圆。

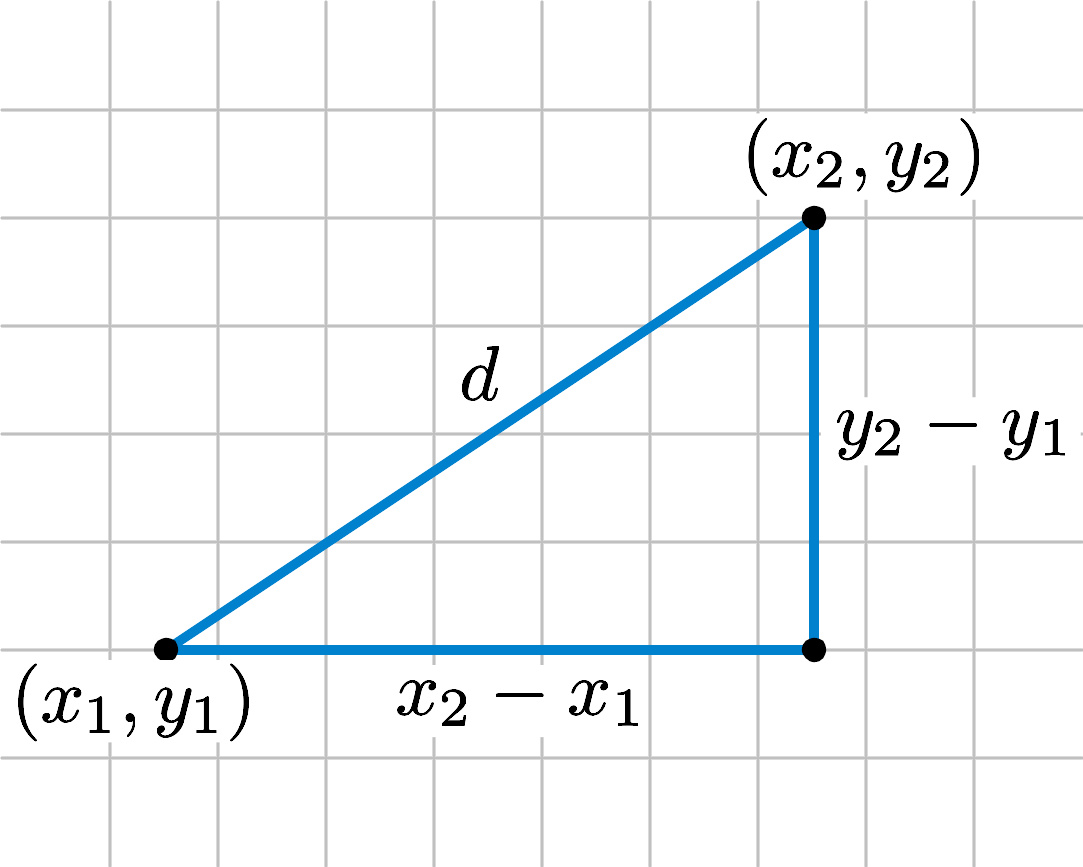
勾股定理的平面距离方程。

距离和角度

在解析几何当中，距离、角度等几何概念是用公式来表达的。这些定义与背后的欧几里得几何所蕴含的主旨相符。例如，使用平面笛卡儿坐标系时，两点A(x1, y1),B(x2, y2)之间的距离d(又写作|AB|被定义为

上述可被认为是一种勾股定理的形式。类似地，直线与水平线所成的角可以定义为

其中 m 是线的斜率。

变化

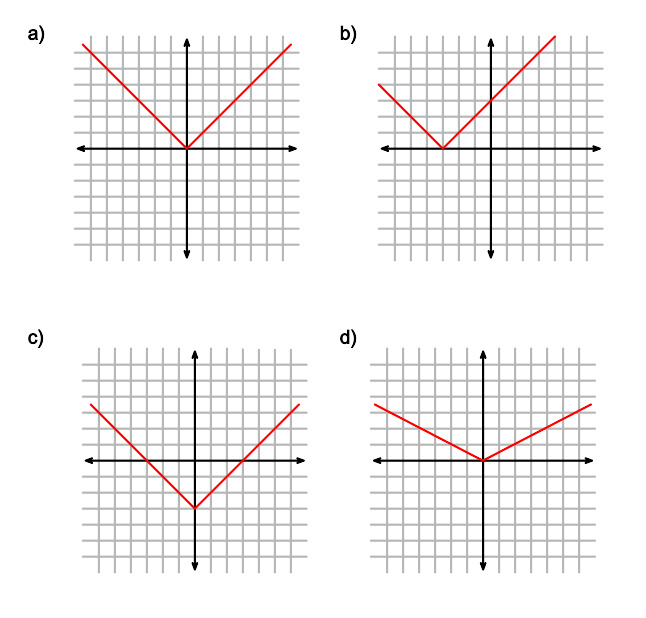
a)y=f(x)=|x|b)y=f(x+2)c)y=f(x)− − -->3d)y=12f(x){\displaystyle {\begin{array}{ll}a)y=f(x)=\left|x\right|&b)y=f(x+2)\\c)y=f(x)-3&d)y={\frac {1}{2}}f(x)\\\end{array}}}

变化可以使母方程变为新方程，但保持原有的特性。例如，母方程 y=1x{\displaystyle y={\frac {1}{x}}} 有水平和垂直的渐近线，处在第一和第三象限当中能够，它所有的变形都有水平和垂直的渐近线，出现在第一或第三、第二或第四象限当中。总的来说，如果 y=f(x){\displaystyle y=f(x)}，那么它可以变为 y=af[b(x− − -->k)]+h{\displaystyle y=af[b(x-k)]+h}。新的变形方程，a{\displaystyle a} 因素如果大于1，就垂直拉伸方程；如果小于1，就压缩方程。如果a{\displaystyle a} 值为负，那么方程就反映在 x{\displaystyle x}-轴上。 b{\displaystyle b} 值如果大于1就水平压缩方程，小于1就拉伸方程。与a{\displaystyle a}一样，如果为负就反映在y{\displaystyle y}-轴上。k{\displaystyle k} 和 h{\displaystyle h} 值为平移，h{\displaystyle h}值是垂直，k{\displaystyle k} 为水平。h{\displaystyle h} 和 k{\displaystyle k} 的正值意味着方程往数轴的正方向移动，负值意味这往数轴的负方向移动。

变化可以应用到任意几何等式中，不论等式是否代表某一方程。 变化可以被认为是个体处理、或是组合处理。

例如，R(x,y){\displaystyle R(x,y)} 在 xy{\displaystyle xy} 平面上

x2+y2− − -->1=0{\displaystyle x^{2}+y^{2}-1=0}

指代单位圆。 图像 R(x,y){\displaystyle R(x,y)} 可以被变化为：

将 x{\displaystyle x} 变为 x− − -->h{\displaystyle x-h} ，使得图像向右移动 h{\displaystyle h} 个单位。

将 y{\displaystyle y} 变为 y− − -->k{\displaystyle y-k}，使得图像向上移动 k{\displaystyle k} 个单位。

将 x{\displaystyle x} 变为 xb{\displaystyle {\frac {x}{b}}}，使得图像以 b{\displaystyle b}值拉伸。 (想象一下x{\displaystyle x} 被膨胀了)

将 y{\displaystyle y} 变为 ya{\displaystyle {\frac {y}{a}}}，使得图像垂直拉伸。

将 x{\displaystyle x} 变为 xcos⁡ ⁡ -->A+ysin⁡ ⁡ -->A{\displaystyle x\cos A+y\sin A}，将 y{\displaystyle y} 变为 − − -->xsin⁡ ⁡ -->A+ycos⁡ ⁡ -->A{\displaystyle -x\sin A+y\cos A}，使得图像旋转 A{\displaystyle A} 个角度。

在基础的解析几何中，不会考虑太多的变化，例如偏移。更多信息请参阅仿射变换。

交集

虽然本讨论仅限于xy-平面上，但它可以很容易地衍生为更高维的空间中。两个几何对象P 和 Q 指代 P(x,y){\displaystyle P(x,y)} 和 Q(x,y){\displaystyle Q(x,y)}，其交集是所有点 (x,y){\displaystyle (x,y)} 的集合。 例如，P{\displaystyle P} 可以是半径为1的圆，圆心在 (0,0){\displaystyle (0,0)}: P={(x,y)|x2+y2=1}{\displaystyle P=\{(x,y)|x^{2}+y^{2}=1\}} , Q{\displaystyle Q} 可以是半径为1的圆，圆心在 (1,0):Q={(x,y)|(x− − -->1)2+y2=1}{\displaystyle (1,0):Q=\{(x,y)|(x-1)^{2}+y^{2}=1\}}。两圆的交叉点是满足方程的所有点的集合。点 (0,0){\displaystyle (0,0)} 是否满足方程呢？将(0,0){\displaystyle (0,0)} 带入 (x,y){\displaystyle (x,y)}，Q{\displaystyle Q} 便成为 (0− − -->1)2+02=1{\displaystyle (0-1)^{2}+0^{2}=1} 或 (− − -->1)2=1{\displaystyle (-1)^{2}=1} ，结论为真，因此 (0,0){\displaystyle (0,0)} 在 Q{\displaystyle Q} 上。换句话来说，接着将 (0,0){\displaystyle (0,0)} 带入 (x,y){\displaystyle (x,y)} ，方程 P{\displaystyle P} 成为 02+02=1{\displaystyle 0^{2}+0^{2}=1} 或 0=1{\displaystyle 0=1}，结论为假。(0,0){\displaystyle (0,0)} 不在 P{\displaystyle P} 上，因此不是它的集合。

P{\displaystyle P} 与 Q{\displaystyle Q} 的交集可以通过同时解方程来求得：

{x2+y2=1(x− − -->1)2+y2=1{\displaystyle {\begin{cases}x^{2}+y^{2}&=1\\(x-1)^{2}+y^{2}&=1\\\end{cases}}} 解得 {x=12y=± ± -->32{\displaystyle {\begin{cases}x={\frac {1}{2}}\\y=\pm {\frac {\sqrt {3}}{2}}\\\end{cases}}}

我们的交集有两点：

就圆锥曲线而言，交集可能会出现至多4个点。

截距

被广泛研究的一种交集是几何对象与 x{\displaystyle x} 和 y{\displaystyle y} 坐标轴的交集。

几何对象与 y{\displaystyle y}-轴的交集被称之为对象的 y{\displaystyle y}-截距。与x{\displaystyle x}-轴的交集被称之为对象的 x{\displaystyle x}-截距。

就线 y=mx+b{\displaystyle y=mx+b}而言，参数 b{\displaystyle b} 定义线在何处与 y{\displaystyle y} 轴相交。据此，b{\displaystyle b} 或 (0,b){\displaystyle (0,b)} 点被称之为 y{\displaystyle y}-截距。

主题

解析几何中的重要问题：

向量空间

平面的定义

距离问题

点积求两个向量的角度

外积求一向量垂直于两个已知向量（以及它们的空间体积）

交点问题

Ax2+Bxy+Cy2+Dx+Ey+F=0{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}. 如果Bxy{\displaystyle Bxy}被考虑进去的话，就会常常用到旋转。这些问题常涉及到线性代数。

例子

下面是美国初中数学竞赛(USMTS)中的题，可以用解析几何来解：

问题：在凸面五边形 ABCDE{\displaystyle ABCDE}中，边长为 1{\displaystyle 1}, 2{\displaystyle 2}, 3{\displaystyle 3}, 4{\displaystyle 4}, 5{\displaystyle 5}，虽然顺序不一定如此。设F{\displaystyle F}, G{\displaystyle G}, H{\displaystyle H}, I{\displaystyle I} 成为 AB{\displaystyle AB}, BC{\displaystyle BC}, CD{\displaystyle CD}, DE{\displaystyle DE} 的各个中点。 设 X{\displaystyle X} 为线段 FH{\displaystyle FH}的中点, Y{\displaystyle Y} 为线段 GI{\displaystyle GI} 的中点。线段 XY{\displaystyle XY} 的长度为整数。求边 AE{\displaystyle AE} 的所有可能长度。

解： 为了不失一般性，假设 A{\displaystyle A}, B{\displaystyle B}, C{\displaystyle C}, D{\displaystyle D}, E{\displaystyle E} 为 A=(0,0){\displaystyle A=(0,0)}, B=(a,0){\displaystyle B=(a,0)}, C=(b,e){\displaystyle C=(b,e)}, D=(c,f){\displaystyle D=(c,f)}, E=(d,g){\displaystyle E=(d,g)}。

应用中点公式，点 F{\displaystyle F}, G{\displaystyle G}, H{\displaystyle H}, I{\displaystyle I}, X{\displaystyle X}, Y{\displaystyle Y} 位于

使用距离公式，

以及

由于 XY{\displaystyle XY} 为整数，

(见同余) 因此 AE=4{\displaystyle AE=4}.

现代解析几何

解析簇(analytic variety)定义为几个解析函数的共同解集。类似与实数与复数的代数簇。任何复流形都是一种解析簇。由于解析簇可能有奇点，但不是所有解析簇都是复数。.

解析几何总体上来说等同与实数与复数代数几何，让-皮埃尔·塞尔在他的著作《代数几何与解析几何》(Géometrie Algébrique et Géométrie Analytique)阐述了这个观点。然而，两个领域依然有其独特性，而证明方式也十分不同，代数几何也包括几何的有限特征。

引述

著作

Katz, Victor J., A History of Mathematics: An Introduction (2nd Ed.), Reading: Addison Wesley Longman, 1998, ISBN 0-321-01618-1 

Boyer, Carl B., History of Analytic Geometry, Dover Publications, ISBN 978-0486438320 

Cajori, Florian, A History of Mathematics, AMS, ISBN 978-0821821022 

Struik, D. J., A Source Book in Mathematics, 1200-1800, Harvard University Press, ISBN 978-0674823556 

文献

Boyer, Carl B. Analytic Geometry: The Discovery of Fermat and Descartes, Mathematics Teacher 37, no. 3 (1944): 99-105

Boyer, Carl B., Johann Hudde and space coordinates 

Bissell, C. C., Cartesian geometry: The Dutch contribution 

Pecl, J., Newton and analytic geometry 

Coolidge, J. L., The Beginnings of Analytic Geometry in Three Dimensions 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。