历史

1935年开始，伯莎·斯威尔斯（Bertha Swirles）提出了多电子体系的相对性处理方法，尽管保罗·狄拉克于1929年在文章中如此提到：

原先理论化学家基本上同意狄拉克的看法，然而1970年代人们开始认识到重元素的相对论效应。1926年，在那篇著名的文献中，奥地利量子物理大师薛定谔提出了不考虑相对论的薛定谔方程。科学家对薛定谔方程作了相对论性的修正（参见克莱因-戈尔登方程），以解释原子光谱的精细结构，然而这类修正并没有很快融入化学研究中，因为原子谱线主要属于物理学而不是化学。多数化学家对相对论量子力学并不熟悉，而且当时化学研究的重点是有机化学（主要是典型的轻元素）。

狄拉克的观点（相对论量子力学在化学中所扮演的角色）是错误的，有两个原因：首先是s轨道和p轨道中的电子速度可与光速相比拟，其次是相对论效应对d轨道和f轨道的间接影响十分显著。正因为这种错误的观点，相对论量子化学在几十年里始终不受重视。

20世纪80年代中期之后的十几年间，以德国为主的欧洲各国理论化学家开始对相对论量子化学进行深入研究，大大发展了理论、程序以及应用，促进了理论和计算化学的发展。现在的相对论量子化学，正在使四分量完全相对论方法的计算量减少，二分量准相对论方法的准确性提高，并向高精度相对论性密度泛函理论、多电子体系的量子电动力学效应、相对论哈密顿算法与从头计算相结合等方向发展。

定性处理

简化的狭义相对论处理

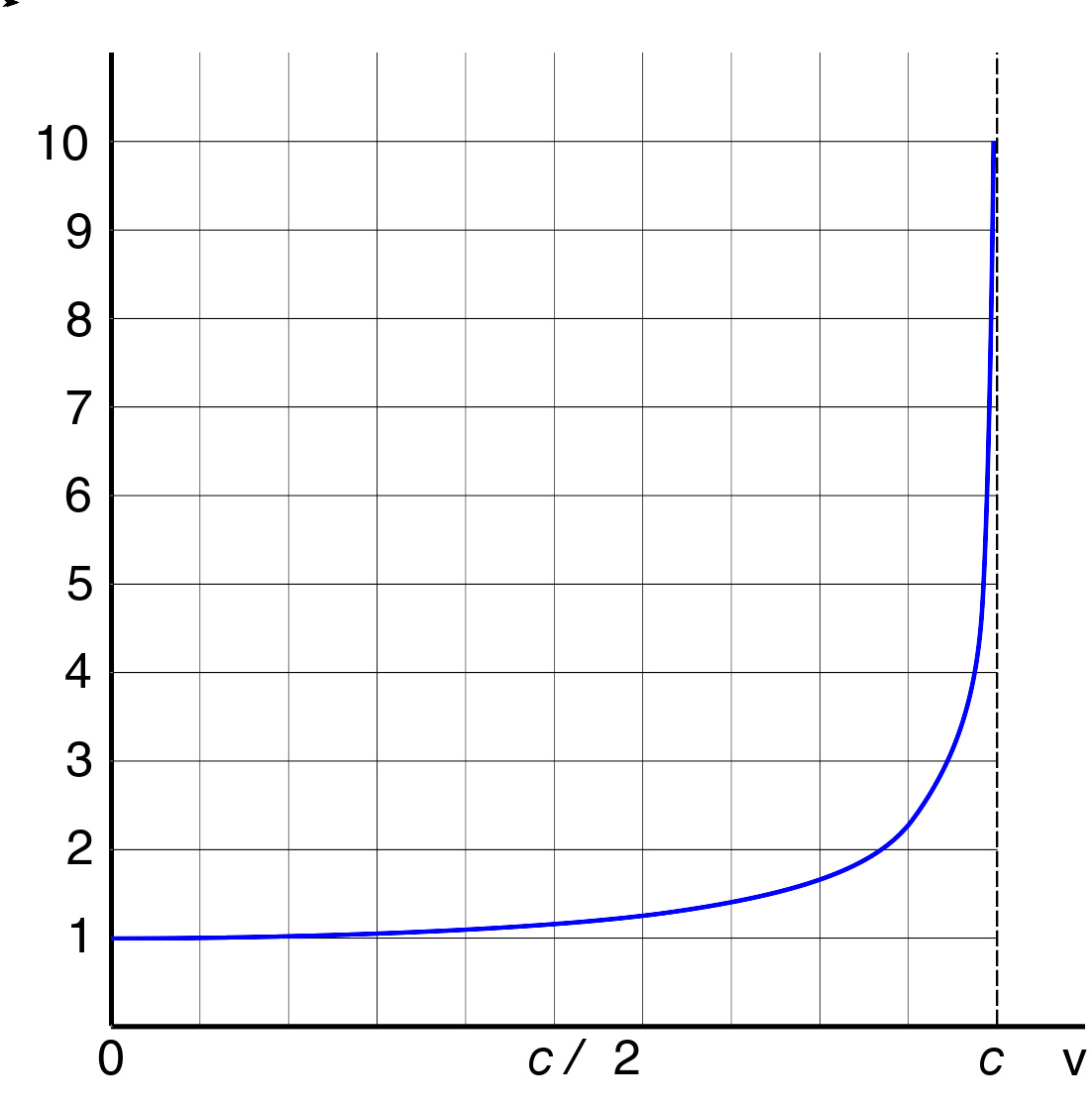
  电子的相对论质量与速度的函数关系。低速时， m r e l {\displaystyle m_{rel}} 与 m 0 {\displaystyle m_{0}} 近似相等， 但是 v e → → --> c {\displaystyle v_{e}\to c} 时 m r e l {\displaystyle m_{rel}} 趋向于无穷大。

相对论最重要的结论之一是电子的相对论质量随速度的增加而增大：

其中 m e , v e , c {\displaystyle \displaystyle m_{e},v_{e},c} 分别是电子的静止质量、速度以及光速。右图说明了相对论效应对电子质量的影响。

这对玻尔半径( a 0 {\displaystyle \displaystyle a_{0}} )有直接影响，因为它的表达式包含质量：

其中 ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数而 α α --> {\displaystyle \alpha } 是精细结构常数（相对论对玻尔模型的修正）。

阿诺·索末菲计算了氢原子的电子（轨道半径为0.0529nm）的精细结构常数 α α --> ≈ ≈ --> 1 / 137 {\displaystyle \alpha \approx 1/137} 。也就是说，精细结构常数说明氢的电子速度大约为光速的1/137。对该式进行扩展，可近似得出更重原子的电子运动速度 v ≈ ≈ --> Z / 137 ∗ ∗ --> c {\displaystyle v\approx Z/137*c} （其中v是它的径向速度）。下面以金（ Z = 79 {\displaystyle Z=79} ）为例子，它的电子的速度将是光速的58%（ α α --> = 0.58 ∗ ∗ --> c {\displaystyle \alpha =0.58*c} ）。将该数据代入并算出 v / c {\displaystyle v/c} ，可得该电子的相对论质量 m r e l = 1.22 m e {\displaystyle m_{rel}=1.22m_{e}} ，反过来将它代入玻尔半径的表达式又可算出轨道半径收缩了22%。

将相对论质量的表达式代入可得经修正的玻尔半径计算公式：

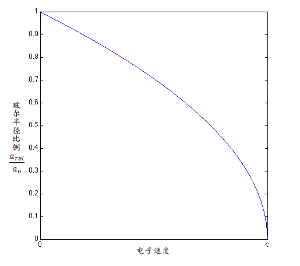
  相对论与非相对论玻尔半径之比和电子速度的函数关系

因此可以认为：

在右图中画出了考虑相对论与非相对论玻尔半径之比关于电子运动速度的函数。请注意重元素相对论模型中的玻尔半径下降越来越快。

将相对论的尺缩效应运用到6s轨道时可得出相同的结果。长度收缩可以用下式来表示：

因此6s轨道的半径收缩到

当引入量子化概念的玻尔理论扩展到类氢原子时，玻尔半径如下所示：

其中 n {\displaystyle n} 是主量子数，Z则是原子序数。根据量子力学理论给出的角动量： m v e r = n ℏ ℏ --> {\displaystyle mv_{e}r=n\hbar } 。将此代入上面的方程可以求解出 v {\displaystyle v} 。

因此原子单位制可简化成下面的表达式：

将上式代入相对论与非相对论玻尔半径之比的计算公式可得：

由上述推导可知主量子数较小而原子序数较大时， a r e l a 0 < 1 {\displaystyle {\frac {a_{rel}}{a_{0}}}<1} 。这符合直觉，即主量子数较小的电子在靠近原子核的空间中概率密度更高。核电荷数较大的原子核外电子运动速度较快。电子的高速运动意味着相对论质量的增加，因此电子概率原子核的概率将更大，从而导致了轨道收缩，引起一系列物理性质和化学性质的变化。

DCB哈密顿算符

狄拉克-库仑-布雷电子哈密顿算符（英语：Dirac-Coulomb-Breit Electronic Hamiltonian，简称DCB哈密顿算符）是量子化处理的基础。对于核势为Vn的电子，它可以表示为：

单粒子的狄拉克哈密顿算符为：

双粒子的哈密顿算符为：

hB存在其他的与频率相关的表示形式。在库仑规范中，磁矢势为 A {\displaystyle \mathbf {A} } ，令 ∇ ∇ --> ⋅ ⋅ --> A = 0 {\displaystyle \nabla \cdot \mathbf {A} =0} 。然后电子间的相互作用就可以视作瞬时的。在除了单斯莱特行列式和自洽场的相关计算中，应当加入类电子投影算符 P {\displaystyle P} ：

但是这样的描述并完整，例如此篇同行评审中讨论了荒木（Araki）概念和量子电动力学概念。然而，对于Z>50的重元素，这两种方法都不如DCB哈密顿算符准确。

分类

其影响分成三种：自旋-轨道作用、直接相对论效应和间接相对论效应。

施瓦茨等人将相对论效应对电子的直接影响视作离原子核距离的函数，他们发现绝大部分的相对论效应都直接来自最内层半波（相对于ns价轨道的就是轨道）。而德默等人之前对自旋-轨道作用的研究表明，对于np价轨道，自旋-轨道作用主要来自最内层的类2p轨道。

由于原子轨道的正交性，轨道收缩必然引起其他s轨道的收缩。原子轨道的正交性是指同一原子两个原子轨道的重叠积分的数值为0：

通过上式进行数学推导并绘制原子轨道等值线图可证明，由于空间分布不同，p、d、f轨道不一定相应收缩，也就是间接相对论效应。

计算

相对论量子化学的计算方法很多，在精确性和计算效率方面各有利弊。除了上文所述的哈密顿方法，还有狄拉克-哈特里-福克方法、矩阵表示法等等。

狄拉克-哈特里-福克方法（简称DHF方法）需要使用极大极小变分原理。这是因为狄拉克方程存在负能连续态，导致狄拉克算符没有下界。因此，需要引入二次量子化的形式，即使用满足下列关系的反对易关系的产生（ a p + = a p {\displaystyle a_{p}^{+}=a^{p}} ）与湮灭（ a p {\displaystyle a_{p}} ）算符和场算符：

场算符 Ψ Ψ --> ( 1 ) = ψ ψ --> ( r 1 ) a p , 〈 〈 --> ψ ψ --> p | ψ ψ --> q 〉 〉 --> = δ δ --> p q {\displaystyle \Psi (1)=\psi (\mathbf {r} _{1})a_{p},\quad \langle \psi _{p}|\psi _{q}\rangle =\delta _{pq}}

通过这样，可以将一次量子化的哈密顿算符改写为二次量子化的哈密顿算符：

而矩阵表示则是使用有限基组将算符离散化。相对论效应起源自原子核附近的高电势处，所以选择的旋量基底必须能够较好地描述中心场狄拉克函数在原子核周围的运动。而这是由原子核电荷分布的模型和旋量函数的变换所决定的。中心场能量本征函数的形式如下所示（其中 P n κ κ --> ( r ) {\displaystyle P_{n\kappa }(r)} 和 Q n κ κ --> ( r ) {\displaystyle Q_{n\kappa }(r)} 为实函数，n为主量子数）：

关于计算方法的细节，请阅读相关文献和专著。

原子内的变化

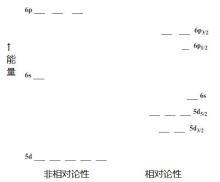
  电子亚层分裂

轨道能量

考虑相对论效应时，s轨道的能量显著下降，p轨道的能量也有所下降。这增强了屏蔽效应，导致d轨道和f轨道的能量的上升。这样的变化结果就是轨道之间的能量差明显增大。

电子亚层分裂

由于自旋-轨道作用，角量子数l>0的电子亚层将分裂成两个亚组，l分别为+1/2和-1/2，其中前者的能量下降。

径向变化

根据狭义相对论，电子高速运动时质量会增大，而电子与原子核之间的库仑力不变，因此它运行的轨道半径会减小。s轨道的这种轨道收缩最为明显，这会导致键长的缩短和诸多化学性质的变化。

性质的变化

物理性质和化学性质最终都取决于电子的能量和分布。对于重元素，必须考虑相对论效应才能对其性质作出准确描述。元素周期表是科学家们以当时已发现的元素的周期性规律为基础建立的。实际上，以此建立的化学模型给它带来了生命力。然而，第6周期元素（Cs-Rn）与第5周期元素（Rb-Xe）与上一周期元素的物理性质和化学性质有许多差别，显示出明显的相对论效应。金以及电子排布类似的铂和汞的相对论效应特别显著。由于电子排布接近4f和5d全充满电子，这三种元素是除超铀元素以外相对论效应最大的元素。

电子排布

对比第5周期元素和第6周期元素的电子排布，可以发现由于第6周期元素相对论效应明显，价层电子排布由第5周期的4d5s或4d5s变为第6周期的5d6s或5d6s。

第6周期元素基态原子倾向于先填充6s轨道，因为6s轨道因相对论效应而收缩，能级下降。铂更是不顾5d轨道全满的稳定性而选择5d6s填充方式。锝是唯一的例外，因为相对论效应不太明显，而且4d是半满的稳定状态。

物理性质

受相对论效应影响，第6周期过渡金属元素熔点变化更大。其中钨是熔点最高的金属，而汞是熔点最低的金属。因为6s轨道收缩，能量下降，使得本周期元素有6个价轨道，这些轨道中的电子都能参与形成金属键。由于这些价轨道和配位环境的对称性很高，每个轨道都能有效成键，不会形成非键轨道。平均每个原子形成3个成键轨道和3个反键轨道。

从铯到钨，电子全部填入成键轨道组合成的能带，能量降低，金属键增强，熔点升高。而从钨到汞，电子填入反键轨道，能量升高，金属键减弱，熔点下降。汞的成键轨道和反键轨道全部填满，金属键很弱，因此在常温下就呈液态。

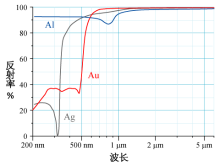
  铝(Al)、银(Ag)和金(Au)镜面的光谱反射率曲线

金、银和铝的反射率已经在右图中给出。人眼会看到波长大约为600纳米的电磁波，即黄光。从金的光谱反射率曲线中可得出，金呈黄色的原因显然是它吸收除黄光以外的其他色光，并将黄光反射到观察者眼中。

电子从5d能级到6s能级的跃迁导致了这种现象。银的电子也能发生类似的跃迁，但是银的相对论效应比金小得多，尽管4d轨道略微扩张、5s轨道略微收缩，4d-5s的能量差仍然远大于金原子中5d-6s的能量差。因此，如果不考虑相对论效应，金应当是白色的，这显然与事实矛盾。相对论效应使得5d轨道能量上升，而6s轨道能量降低，减小了能隙。近期才完成的金的介电常数理论计算也表明，不考虑相对论效应的话金的吸收带将移动至紫外区，呈现与银类似的白色。金属铯作为能获得可观察量的最重碱金属，也显现出相对论效应的影响。其他碱金属都是银白色，而金属铯呈现出独特的银金色。

除了过渡元素以外，相对论效应对主族元素也有一定影响。例如Bi(C6H5)5的紫色和PbCl6的黄色就是相对论效应引起的LUMO稳定化造成的，因为类似的锑和锡化合物是无色的。亚硝酸铅则不同，它的颜色是亚硝酸根的单线态-三线态转化与铅离子的自旋-轨道作用共同作用的结果。

第6周期元素

汞

汞（Hg）在常温下（凝固点-39 °C）是一种液体，也是惟一一种常温下呈液态的金属。汞的金属键与附近的元素（镉的熔点为321 °C，金更高达1064 °C）相比特别弱。镧系收缩效应可以部分解释该问题，但它不能完整地说明这种反常现象。在气相中的汞也与其他金属不同，它大部分以单原子形式Hg(g)存在，Hg2(g)也存在，因为键长的相对缩短使它变得稳定。

Hg2(g)不存在，因为6s轨道由于相对论效应而收缩。因此它对任何化学键的形成只有微弱作用。实际上Hg-Hg键的主要成分是范德华力，这也解释了Hg-Hg键如此之弱的原因，这导致了它在室温呈液态。Au2(g)和Hg(g)是类似的，至少与H2(g)和He(g)具有类似的外层电子。因为相对论效应引起的轨道收缩，具有6s结构的气态汞可被称作伪惰性气体。

相对论效应也使汞表现出比同族元素更高的氧化态，能形成四氟化汞等化合物。三氟化汞本身是不稳定的，但它的二聚体Hg2F6和配合物HgF4可能是稳定的。理论研究表明，高价汞烷（HgH4和HgH6）有可能存在，因为等电子体PtD4和AuH4已有报道。

金

金能形成Au2分子和Au离子。同族的银在液氨中能形成Ag，在气相中也能形成Ag2，但都明显没有“元素态”金属金的稳定。虽然碱金属也能形成类似的物质，但碱金属负离子只有在大环配体穴醚中才能稳定存在。CsAu可以溶解在液氨中，缓慢除去溶剂得到非常活泼的蓝色固体CsAu·NH3。金负离子的存在已经被包括穆斯堡尔谱学在内的多种方式证明。相对论效应对导电性也有影响，现在已知金化铯是半导体，而如果不考虑相对论效应，它会是一种导体。

金负离子被认为是一种拟卤素离子：

金在碱作用发生歧化反应：

金能与氢原子形成共价键：

金有+5氧化态，这是同族元素没有的。最近甚至合成一种化学式为AuF7的化合物，光谱学研究表明它是一种双氟配合物。如果能证实，这将是第一个氟分子作路易斯碱的例子。

此外金还能与稀有气体氙形成特殊的AuXe42+、顺式AuXe2（结构类似于二氧化氙）、XeAuFAuXe、(F3As)AuXeC等多种离子 ，其中两种惰性的元素之间形成了化学键。研究表明，可以检测到氙的电子云向金部分偏移，这可以解释为相对论效应的影响。金能形成大量的原子簇化合物，例如Au55和Au2Te12，它们的对称性较差就是相对性效应的结果。

铂

铂能形成Pt离子，该离子存在于下文介绍的Cs2Pt中。Pt2是Hg2和Au2的等电子体。BaPt中不含有这种离子，而是通过Pt-Pt键形成了链状化合物。电荷迁移研究表明，每个钡原子只向铂原子提供了一个电子，这种物质被认为是第一种含有过渡金属津特耳（Zintl）离子的化合物。固态Ba3Pt2中哑铃形的p电子云重叠形成Pt-Pt键，而Ba2Pt采用氯化镉型结构，该化合物的结构可以写成(Ba)2Pt·2e。电化学和X射线光谱学研究证明其中铂的氧化态确实为负值。

相对论效应增加了Pt(VI)化合物的稳定性，尽管它们依然是强氧化剂。六氟化铂的电子亲和能为7电子伏特，能够得电子形成PtF6和PtF6。到现在为止，尽管理论计算表明六氟化钯是稳定的，但还没有任何关于Pd(VI)化合物的报道，这可能与4d电子的相对论效应较弱有关。

理论计算表明，八氟化铂是不稳定的，因为在很低的温度它还能自发地分解产生氟。在10K下，使用激光消融技术在氩和氧的混合物中处理铂原子，产生具有D3h对称性的三氧化铂。在气相中或使用基质隔离技术，铂还能结合稀有气体原子形成依靠范德华力结合的超分子Ng-Pt-Ng（Ng代表稀有气体原子）。

其他过渡元素

铱能形成反常的+8氧化态化合物四氧化铱，理论计算甚至表明+9氧化态的[IrO4]可能存在。

关于更多元素的氧化态，可参阅这篇综述。

p区元素

第6周期p区元素受到相对论效应影响，6s电子对难以电离，被称作惰性电子对效应。这使得铊、铅和铋的稳定氧化态分别为+1、+2和+3，比主族数低了2（放射性元素研究较少）。不仅如此，p区元素在一些特殊的化合物能呈现出更低的氧化态，这是较轻同族元素所罕见的。

铊能与碱金属形成金属互化物M6Tl6（M=K、Rb、Cs），其中Tl6由于四方畸变而具有D4h对称性。而BaTl3中有明显的Tl-Tl相互作用。其他更加复杂的铊原子簇阴离子也有报道（例如：K6Tl17）。

铅能形成多种原子簇阴离子，其中最常见的就是Na4Pb9中的Pb9。铅与碱金属形成的最稳定的合金中原子个数比均在1：4左右。惰性电子对效应导致铅的四氟化物很不稳定，只有四氟化铅在室温下稳定，四氯化铅在此温度下缓慢分解。四溴化铅和四碘化铅只有在超低温下才能通过基质隔离技术制得，虽然有其他制法的报道但都未被确认。

铋也能形成多种金属互化物，而且能形成单原子的Bi离子，例如符合化合价的Na3Bi。在M11Bi10（M=Sr、Ba）还含有较复杂的Bi2和Bi4。虽然理论上存在，但是目前没有发现真正的-1氧化态铋化合物。铋的+1氧化态存在于溶液和Bi10Hf3Cl18中，但是一卤化铋中含有铋原子簇，因此不是严格意义上的+1氧化态。含有Bi2分子的化合物也已制得。

s区元素

铯是一种典型的碱金属，相对论效应对它的影响很小。它与钠、钾、铷一样都能形成碱金属负离子Cs。有报道称在铯化物中可能存在三原子阴离子Cs3。铯能与铂形成金属间化合物Cs2Pt，其中含有Pt离子。这种深红色的固体采用Ni2In型结构，每个铂原子周围有九个铯原子，形成三冠三棱柱形的配位多面体。

钡能与铂形成特殊的金属间化合物Ba2Pt。每个钡原子都只向铂提供一个电子，说明6s轨道的稳定性有所上升。实验发现，Ba和Ba2的极化率都与考虑相对论效应的计算符合得很好。

第7与第8周期元素

s区元素

第7与第8周期元素都是放射性元素，许多种元素还没有获得。这使得对它们的研究十分困难，但理论计算已经证明它们受相对论效应的影响比第6周期元素更显著。事实上，只有钫、氡、鎶三种元素的相对论效应有过较多的研究。

理论计算表明，钫和镭的电负性甚至比上一周期的铯和钡大，这与元素周期律的推测恰好相反。这造成了CsFr分子中电子云偏向钫，以及钫的氧化物比铯具有更大的共价性。镭的性质也因电负性的反常变化而变化。

过渡元素

通常认为铀的最高氧化态为+6，然而计算表明六氧化铀可能存在，但氧化态并不是+12。其中具有D2h对称性的D2h-UO2(η-O2)2能量最低，氧化态为+8。

对超重元素相对论效应的研究较少，其中主要的信息如下。对于超重元素，由于受相对论效应的强烈影响，它们的化学性质和元素周期律推断的结果有一定差别。

?（Db）元素的7s电子轨道相对收缩了25%。?（Sg）元素和同族的铬、钼、钨相比，它的7s轨道与6d轨道的能级顺序发生了反转，其结果是7s轨道能量比6d轨道能量还低。将鎶吸附在金表面，与其他放射性同位素进行比较，发现它的沸点在汞和氡之间。鎶与卤素形成的共价键比汞更弱，也说明了它的相对论效应比汞更明显。

p区元素

p区重元素受相对论效应影响同样明显。例如第118号元素Og可能不是惰性气体，而且是一种固体。甚至有计算表明它的电子亲和能为+0.064eV，也就是说，它可能形成前7周期元素中最大的单原子阴离子Og。

扩展阅读

（英文）Christiansen, P A; Ermler, W C; Pitzer, K S. Relativistic Effects in Chemical Systems. Annual Review of Physical Chemistry. 1985-10-01, 36 (1): 407–432. doi:10.1146/annurev.pc.36.100185.002203. 

（英文）Pyykko, Pekka. Relativistic effects in structural chemistry. Chemical Reviews. 1988-05-01, 88 (3): 563–594. doi:10.1021/cr00085a006. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。