历史

自17世纪发现牛顿万有引力定律以来，从拉普拉斯开始，就有许多数学家全神贯注太阳系的稳定性。二体问题近似解的稳定轨道忽略其它天体的影响。在太阳系中添加其它天体的相互作用对稳定性造成的影响很小，但是首先不知道在很长的周期中添加会造成何种轨道参数的改变和不同的配置，或是其它一些稳定的影响是否能维持行星轨道的配置。

拉普拉斯是最先找到解释伽利略卫星奇异舞蹈（见下文）答案的人。持平而论，自当时迄今以来，在这个领域的研究是非常活跃的，但是仍有许多待解决的问题（例如，在巨大行星的环，环中的小卫星和微粒的相互作用如何维系环）。

共振的类型

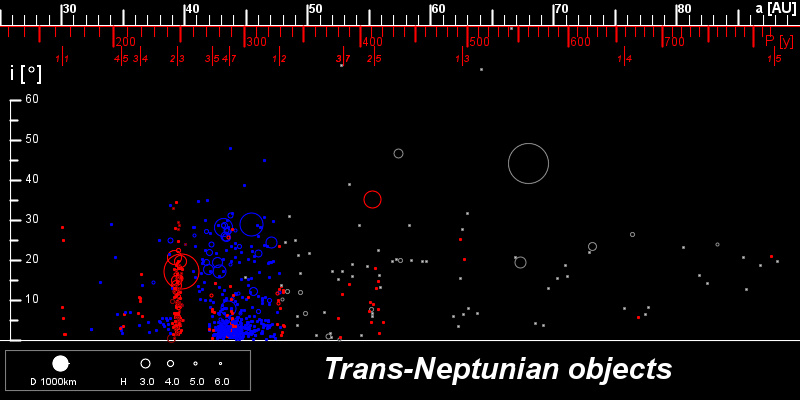
  对照于那些QB1（蓝色）和非共振（或不知道是否共振）的离散盘天体（灰色），共振海王星外天体（红色）的半长轴聚集在与海王星的低整数共振（接近顶端的垂直红色条）。

通常，轨道共振可能

涉及一个或任何组合的轨道参数（例如，离心率相对于半长轴，或轨道倾角）。

从短期的任何时间尺度来看，在10至10年的长期测量都有其通约性。

导致即使长期稳定运行的轨道，也有可能造成不稳定性。

平均运动轨道共振发生在两个天体的公转周期，其中一个的周期是对方的简单整数比。依据详细的的资料，这可以使轨道稳定，也可以使轨道被摧毁。当这两个天体在这种同步的运动中没有密切接触时，可能会出现稳定。例如：

无论与海王星多么接近，冥王星和冥族小天体的轨道都是稳定的，因为它们与海王星是3:2的共振。共振可以确保当它们接近近日点和海王星的轨道时，海王星是在相当远的距离之外（平均有它的轨道距离的四分之一）。其它没有共振的近海王星天体（数量更多）会被海王星强大的摄动从这个区域逐出。还有规模较小，但是很明确有着1:1共振的共振海王星外天体（海王星特洛伊）、3:5（周期约275年）、4:7（周期约290年）、1:2（周期约330年）、和2:5（周期约410年），除此之外，在海王星之外还有其它的。

在距离太阳3.5AU以内的小行星带，有与木星有着3:2、4:3、和1:1的族群分布着（特别是希尔达族、（279）图勒、和特洛伊天体）。

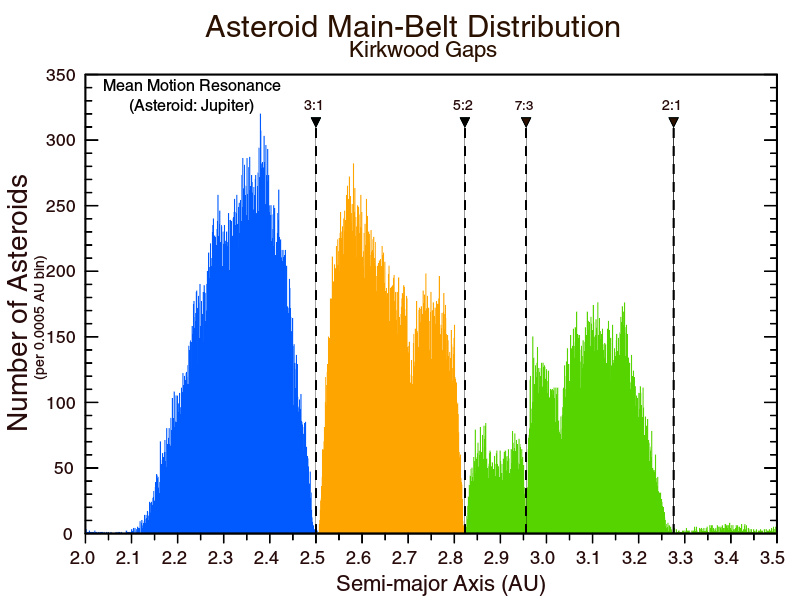
 小行星轨道半长轴的分布图，显示出因为与木星共振造成不稳定的柯克伍德空隙。

  在土星环的螺旋密度波是环内的卫星所激起的共振。这些波从土星（左上方）向外传播，位于中心正下方最大的波与土卫十有着6:5的共振。

轨道共振也可以摧毁一个稳定的轨道。对小天体而言，不稳定实际上是更有可能的。例如：

在距离太阳3.5AU以内的小行星带，与木星的主要平均运动轨道共振落在小行星位置分布的空隙，柯克伍德空隙（最显著的是在3:1、5:2、7:3、和2:1的共振）。在这些位置上的小行星因为反复的受到木星的摄动，几乎已经完全被抛空了。然而，还是有少数的小行星目前暂时在或接近这些共振的位置。例如，艾琳达族就为位于或接近3:1共振，而它们的轨道离心率在与木星的相互作用下持续的在增加，直到最终它们会与内侧的行星密切接触，然后将它们从共振轨道弹射出去。

在土星环内，卡西尼缝是 B环和外侧的 A环之间的空隙，与米玛斯有着2:1的共振（更特别的是卡西尼缝内侧边缘惠更斯缝的位置。）。

在土星环，恩克环缝和基勒环缝是与置身在A环内的潘和达佛涅斯1:1共振清空微粒形成的。A环的外侧是由土卫十有着7:6的不稳定共振维系着。

大多数天体中的共振轨道都有着相同的方向，然而有少数是逆行的，达摩克型小行星是被土星或木星捕获，并被发现暂时处在平均运动轨道共振上的小行星。这种轨道的相互作用比轨道在同一方向的机制的相互作用为弱。

拉普拉斯共振发生在三个或更多天体的轨道周期之间有着简单整数比的系统上。例如，木星的佳利美德、欧罗巴、和埃欧轨道的1:2:4轨道共振。系外行星格利泽876e、b、和c，也有1:2:4的轨道共振。

林达博共振导出螺旋密度波不仅适用在星系（恒星是受螺旋臂本身的力支配的），也适用于土星环（环中的微粒是受到土星卫星的力支配）。

长期共振发生于两个轨道的进动同步时（通常是近日点或升交点）。一颗小天体在与大许多的天体（例如行星）长期共振下，将有与大天体相同的速率。长时间（100万年或更长）的长期共振会改变小天体的轨道离心率和轨道倾角。

几个明显的长期共振例子，包括土星都是。土星自转轴的进动和海王星自转轴的进动之间有着共振（两者的周期都长达187万年），已经确定与土星巨大的转轴倾角（26.7°）可能有着相同的来源。最初，土星的倾角大概是比角接近木星（3.1°）。古柏带逐渐的枯竭使海王星的进动减少；最终，两著的频率匹配，而土星的轴向进动进入到自旋－轨道共振，导致土星的倾角增加（海王星轨道的角动量是土星自转的10倍，因此主导著互动的关系。）。

小行星和土星之间的拱点长期共振（ν6 = g -g6）协助塑造出了小行星带。接近它的小行星，离心率会缓慢的增加，直到它们成为接近火星的小行星。此时，它们会因为与火星遭遇而从小行星带弹出。这种共振形成小行星带内部和侧面边界的距离大约是2AU和约20°的轨道倾角。

数值模拟认为水星和木星（g1=g5）之间的拱点长期共振，最终有可能增加水星的离心率，并且可能在今后的数亿年破坏内太阳系。

在土星环C环内的泰坦小环代表着另一种形式的共振，在其中的一个轨道的拱点进动率完全符合另一个的公转速度。这个偏心小环外侧的末端永远朝向土星最大的卫星泰坦。

古在共振发生在对轨道倾角和离心率摄动的同步振荡（增加离心率而同时渐少倾角，反之亦然）。这种共振仅适用于高轨道倾角的天体；因此，这种轨道往往是不稳定的，因为越来越大的离心率会导致近心点变小，因而造成碰撞或被潮汐力破坏（对于大卫星）。

涉及轨道离心率另一种类型的例子是木卫三和木卫四的离心率，即使有着相对的相位，依然有181年的共通变化周期。

在太阳系的平均运动共振

  描绘在旋转框架中，被推测与海王星有着7:12共振的妊神星，图中的海王星（右下方的蓝色小点）被固定不动。妊神星变化著的轨道，对正于海王星会定期的反转（天秤动），保持着共振。

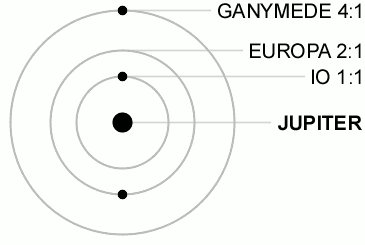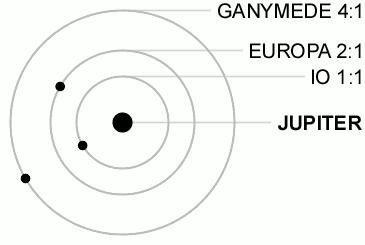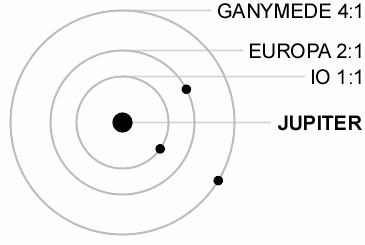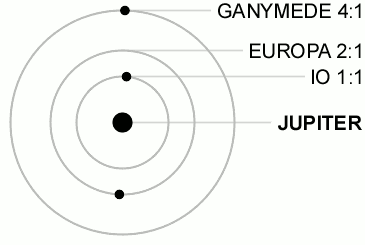
  由三颗伽利略卫星展示的拉普拉斯共振。图中的比率是公转的周期比。

在太阳系内只有少数的平均运动共振，包括行星、矮行星或大的天然卫星是已经知道的（在小行星、行星环、小卫星和更小的古柏带天体，和许多可能的矮行星还会有更多）：

2:4忒堤斯–米玛斯（土星的卫星）

2:3冥王星–海王星

1:2狄俄涅–恩克拉多斯（土星的卫星）

3:4许珀里翁–泰坦（土星的卫星）

1:2:4佳利美德–欧罗巴–埃欧（木星的卫星）

此外，妊神星被认为是与海王星有着7:12的共振，阋神星和鸟神星与海王星分别有5:17和6:11的共振。

周期之间简单的整数比之后，很方便和简化的隐藏了许多更复杂的关系：

合的点可以定义在附近振荡的共振均衡点（天秤动）。

在非零离心率的场合，交点或近日点可以漂移（共振的关联，短周期，不是长期进动）。giv

参考稍后的插图，考虑埃欧-欧罗巴著名的1:2共振。如果轨道周期在这种的关系，平均运动 n {\displaystyle n\,\!} (周期的倒数，通常表示为度/每天）将满足下式：

代入资料（来自维基百科）将可以得到−0.7395° /日，于零有着极大不同的值！

实际上，共振是完美的，但它也涉及近木点（轨道上最接近木星的点）的进动， ω ω --> ˙ ˙ --> {\displaystyle {\dot {\omega }}} 。正确的方程（拉普拉斯方程的一部分）是：

换言之，在考虑到近木点的进动，埃欧的平均运动确实是欧罗巴的两倍。一位者设定在漂移的近木点上的观测者，将看见卫星距角在同一个地点伸展。除了忒堤斯–米玛斯，列在上面的其它对都满足相同类型的方程。在这种情况下，共振满足方程

天秤动的会合点将会围绕在这两颗卫星交点的中间点上。

拉普拉斯共振

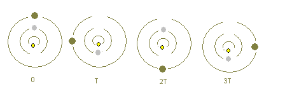
  埃欧、欧罗巴、佳利美德共振的图解。从中心向外依序为埃欧（黄色）、欧罗巴（灰色）和佳利美德（黑色）。

最著名的共振涉及埃欧－欧罗巴－佳利美德，包括下面锁定卫星轨道相位的关系：

此处 λ λ --> {\displaystyle \lambda } 是卫星的平均经度。这种关系使得三重的合是不可能的。图解说明了卫星埃欧在1、2、和3个周期后的位置。（在格利泽876的系统，相较之下，是最外层行星的运行轨道和每一颗行星合的三重关系。）

冥族小天体的共振

矮行星冥王星被困在与海王星有着共振轨道的圈套中，他的共振包括：

平均运动2:3的共振

近日点的共振（大约90°的天秤动），维持近日点在黄道的上方。

近日点共振的经度与海王星相关联

这些共振的一个结果是当冥王星越过海王星的轨道时，两者之间的距离至少在30天文单位以上，而两者之间最小的距离大约是17天文单位，而冥王星和天王星之间的距离最小距离只有11天文单位。（详细的解释和图说请参见冥王星的轨道。)

同样和海王星有着2:3共振的天体，称为冥族小天体，是可能成为矮行星的亡神星。亡神星的轨道离心率和倾角都与冥王星相似，然而与海王星有着相同的共振使它很不自然的总在与冥王星相对的相位上；所以亡神星有时会被描述为反冥王星。

系外行星的平均运动共振

虽然大多数以经被发现的系外行星系统还没有被发现有平均运动共振，但已有一些明显的例子被揭漏：

如前述题道的格利泽876e、b和c，有着1:2:4的轨道共振，周期分别为124.3、61.1和30天。

KOI-730d、b、c和e出现3:4:6:8的共振，轨道周期为19.72、14.79、9.85和7.38天。

KOI-500c、b、e、d和f，出现接近20:27:41:62:193的共振，周期分别为9.522、7.053、4.645、3.072和0.9868天。

KOI-738和KOI-787出现一对7:9共振的行星（比率各自为1/1.285871和1/1.284008）

开普勒37d、c和b出现误差在1%内的5:8:15共振，周期分别为39.792187、21.301886和13.367308天。

系外行星中呈现接近1:2共振平均运动的现象非常普遍。凌日法发现的系统有16%的报告中有这样的事例（周期比例的范围在1.83-2.18）。以多普勒光谱特征发现的系外行星系统也有六分之一的比例（在这种情况下周期比率的范围更窄）。由于对系统的知识还不完整，实际的比例可能会更高。整体而言，约三分之一径向速度系统的特征有一对行星接近通约性。更常见的视一对行星的轨道周期有着接近平均运动共振的比率，不是高了几个百分点就是低了几个百分点（特别是在第一阶的共振，整数上的比率只有一个有不同）。在与恒星有潮汐作用的情况下，这样的预测是很接近真实的。

符合"接近"比率的平均运动

  描绘的是在旋转框架中（2）智神星与木星之间接近18:7的共振（点击观看动画）。木星（在左上角的粉红色椭圆环）平稳的类似固定不动。智神星轨道的漂移与木星对正的方随着时间改变；它没有反转的路径（也就是说没有天秤动）。

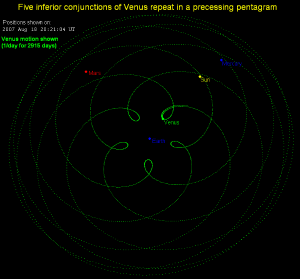
  描绘的是地球：金星接近8:13的共振。地球被固定在非旋转框架图的中心，连续追踪金星的内合超过8个地球年，反映出五角星的模式（数值的比率不同反射出的模式也就不同）。

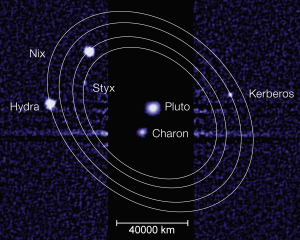
  描绘出冥王星较外面4颗小卫星的轨道，它们遵循着3:4:5:6的序列，相对于最大的卫星卡戎的周期有着近共振。

在行星或主要卫星之间的轨道频率有时会指出有接近整数数值的比率关系（见下面的清单）。然而，这并没有任何动力学上的意义，因为没有适当的近日点进动或其它振动使共振更为完美（详细的讨论参见前节的叙述）。即使这种不匹配相当的小（不同于真正的共振)，这种接近共振的动态还是无意义的，因为在每个周期后，这些天体的相对位置还是会偏移。在天文学的短时间尺度平均值，它们相对的位置是随机的，就像完全不靠近共振状态的机构。例如，考虑地球和金星的轨道，它们在金星公转13周和地球公转8周之后，又配置在轨道上几乎相同的对位置上。正确的比率是0.61518624，和精确的8：13只有0.032%的偏差。在8年后，金星在轨道位置上的偏移只有的1.5°。不过，这依然可以让金星和地球经过120个循环后，也就是960年后，发现彼此在对面的位置上。因此，在数千年或更长时间尺度上（以天文学的标准仍然很小），它们的相对位置实质上依然是随机的。

近共振的存在可能会反映出在过去存在着一个完美的共振，或是系统正朝向完美的共振来演进。

一些轨道频率的巧合包括：

在清单中最值得关注（最不可能）的是木卫一（Io）和木卫十六（Metis）的轨道关系，其次是天卫十三（罗莎琳德，Rosalind）和天卫六（Cordelia，科迪）、智神星和谷神星、木卫四（Callisto）和木卫三（Ganymede）、以及冥卫三（Hydra）和冥卫一（Charon）。

过去的平均运动共振可能

相关条目

（1685）托罗：一颗与地球有着5:8共振的小行星。

（3753）克鲁特尼：与地球1:1共振的小行星。

通约性

德莫特定律

马蹄形轨道：以另一种1:1共振型态跟随着的天体

古在共振

拉格朗日点

水星：3:2的自旋轨道共振

音乐宇宙（"music of the spheres"）

共振海王星外天体

潮汐锁定

潮汐共振

提丢斯-波德定律

特洛伊天体：1:1共振型态的天体

参考文献

书目

C. D. Murray, S. F. Dermott (1999). Solar System Dynamics, Cambridge University Press, ISBN 978-0-521-57597-3.

Renu Malhotra Orbital Resonances and Chaos in the Solar System. In Solar System Formation and Evolution, ASP Conference Series, 149（1998）preprint.

Renu Malhotra, The Origin of Pluto"s Orbit: Implications for the Solar System Beyond Neptune, The Astronomical Journal, 110（1995）, p. 420Preprint.

Lemaître, A. Resonances: Models and Captures. (编) Souchay, J.; Dvorak, R. Dynamics of Small Solar System Bodies and Exoplanets. Lecture Notes in Physics 790. Springer. 2010: 1–62. ISBN 978-3-642-04457-1. doi:10.1007/978-3-642-04458-8. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。