实数的平方根

x的平方根亦可用指数表示，如：

x {\displaystyle x} 的绝对值可用 x 2 {\displaystyle x^{2}} 的算数平方根表示：

正数的平方根

若正整数x是平方数，则其平方根是整数。若正整数x不是平方数，则其平方根是无理数。

对于正数x、y，以下式成立：

负数的平方根

负数的平方根在复数范围内同样有定义。

负数有两个平方根，它们为一对共轭的纯虚数。

以虚数单位 i = − − --> 1 {\displaystyle i={\sqrt {-1}}} 可将负数x的平方根表示为

例如-5的平方根有两个，它们分别为 5 i {\displaystyle {\sqrt {5}}i} 和 − − --> 5 i {\displaystyle -{\sqrt {5}}i} 。

对于负数x、y，以下式成立：

平方根函数

复数的平方根

对于任何一个非零的复数 z {\displaystyle z} 都存在两个复数 w {\displaystyle w} 使得 w 2 = z {\displaystyle w^{2}=z} 。

z {\displaystyle {\sqrt {z}}} 通常定义如下：如果 z = r exp ⁡ ⁡ --> ( i φ φ --> ) {\displaystyle z=r\exp(i\varphi )} （其中 − − --> π π --> ≤ ≤ --> π π --> {\displaystyle -\pi ），则 z = r exp ⁡ ⁡ --> ( i φ φ --> / 2 ) {\displaystyle {\sqrt {z}}={\sqrt {r}}\exp(i\varphi /2)} 。 因此，平方根函数除了在非正实数轴上以外是处处全纯的。 1 + x {泰勒isplaystyle {\sqrt {1+x}}} 的泰勒级数也适用于复数x（|x| < 1）。

如果一个复数是 x + i y {\displaystyle x+iy} 的形式，则可以使用以下公式计算平方根：

因为在虚数里，平方根函数的值不是连续的， z w = z w {\displaystyle {\sqrt {zw}}={\sqrt {z}}{\sqrt {w}}} 这条定律不成立。如果这条定律仍可用，就会出现一些错误的证明，例如：

注意 c 2 = ± ± --> c {\displaystyle {\sqrt {c^{2}}}=\pm c} ，因此 a 2 b 2 = ± ± --> a b {\displaystyle {\sqrt {a^{2}b^{2}}}=\pm ab} ， 所以 z w = ± ± --> z w {\displaystyle {\sqrt {zw}}=\pm {\sqrt {z}}{\sqrt {w}}} ，使用 a = z {\displaystyle a={\sqrt {z}}} 和 b = w {\displaystyle b={\sqrt {w}}} 。

多项式的平方根

例：若 x ∈ ∈ --> R {\displaystyle x\in \mathbb {R} } ， x 4 + 2 x 2 + 1 = ( x 2 + 1 ) 2 = | x 2 + 1 | = x 2 + 1 {\displaystyle {\sqrt {x^{4}+2x^{2}+1}}={\sqrt {(x^{2}+1)^{2}}}=|x^{2}+1|=x^{2}+1\,\!}

符号的演变

古代未有划一的平方根符号时，人们通常使用他们语言内开方这个字的首个字母的变型作为开方号。

拉丁语中的latus（正方形边）的首个字母“L”亦受不少中世纪的欧洲人采用；亨利·布里格斯在其著作Arithmetica Logarithmica则用横线当成latus的简写，在要被开方的数下画一线。

最有影响的是拉丁语的radix（平方根），1220年Leconardo在Practica geometriae使用R（R右下角的有一斜划，像P和x的合体）； {\displaystyle {\sqrt {}}} （没有上面的横划）是由克里斯多福·鲁登道夫在1525年的书Coss首次使用，据说是小楷r的变型；后来数学家笛卡尔给其加上线括号，但与前面的方根符号是分开的（即“√ ￣”），因此在复杂的式子中它显得很乱。直至18世纪中叶，数学家卢贝将前面的方根符号与线括号一笔写成，并将根指数写在根号的左上角，以表示高次方根（当根指数为2时，省略不写。）。从而形成了现在人们熟知的开方运算符号 n {\displaystyle {\sqrt[{n}]{\,\,}}} 。

2的算术平方根

数学史中，最重要的平方根可以说是 2 {\displaystyle {\sqrt {2}}} ，它代表边长为1的正方形的对角线长，是第一个公认的无理数，也叫毕达哥拉斯常数。

2 {\displaystyle {\sqrt {2}}} 是无理数，可由归谬法证明：

设 2 {\displaystyle {\sqrt {2}}} 为有理数，可表示为 p q {\displaystyle {\frac {p}{q}}} ，其中p、q为互质之正整数。

因为 ( 2 ) 2 = p 2 q 2 = 2 {\displaystyle \left({\sqrt {2}}\right)^{2}={\frac {p^{2}}{q^{2}}}=2} ，故 p 2 {\displaystyle p^{2}} 是2的倍数，p也是2的倍数，记为2k，其中k为正整数。

但是 2 q 2 = p 2 = 4 k 2 {\displaystyle 2q^{2}=p^{2}=4k^{2}} ，故 q 2 = 2 k 2 {\displaystyle q^{2}=2k^{2}} ， q 2 {\displaystyle q^{2}} 是2的倍数，q也是2的倍数。

依上两式，p、q都是2的倍数，和p、q为互质之正整数的前题矛盾。依归谬法，得证 2 {\displaystyle {\sqrt {2}}} 不是有理数，即 2 {\displaystyle {\sqrt {2}}} 是无理数。

计算方法

中算开方

  北宋贾宪增乘开平方法

《九章算术》和《孙子算经》都有筹算的开方法。宋代数学家贾宪发明释锁开平方法、增乘开平方法；明代数学家王素文，程大位发明珠算开平方法，而朱载堉《算学新说》首创用81位算盘开方，精确到25位数字。

长除式算法

长除式算平方根的方式也称为直式开方法，原理是 ( a + b ) 2 = a 2 + 2 a b + b 2 = a 2 + ( 2 a + b ) b {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}=a^{2}+(2a+b)b} 。

首先将要开平方根的数从小数点分别向右及向左每两个位一组分开，如98765.432内小数点前的65是一组，87是一组，9是一组，小数点后的43是一组，之后是单独一个2，要补一个0而得20是一组。如1 04.85 73得四组，顺序为1" 04. 85" 73"。

将最左的一组的数减去最接近又少于它的平方数，并将该平方数的开方（应该是个位数）记下。

将上一步所得之差乘100，和下一组数加起来。

将记下的数乘20，然后将它加上某个个位数，再乘以该个个位数，令这个积不大于又最接近上一步所得之差，并将该个个位数记下，且将上一步所得之差减去所得之积。

记下的数一次隔两位记下。

重复第3步，直到找到答案。

可以在数字的最右补上多组的00"以求得理想的精确度为止。

下面以 200 {\displaystyle {\sqrt {200}}} 为例子：

1     4 .     1     4     2 2 | 00.00 | 00 | 00 1   _ _ --> 1 × × --> 1 ≤ ≤ --> 2 1   00 a = 1 0 , b = 4     96   _ _ --> ⇒ ⇒ --> ( 2 a + b ) b = 2 4 × × --> 4 = 96 ≤ ≤ --> 100   4   00 a = 1 4 0 , b = 1   2   81   _ _ --> ⇒ ⇒ --> ( 2 a + b ) b = 28 1 × × --> 1 = 281 ≤ ≤ --> 400   1   19   00 a = 1 4 1 0 , b = 4   1   12   96   _ _ --> ⇒ ⇒ --> ( 2 a + b ) b = 282 4 × × --> 4 = 11296 ≤ ≤ --> 11900     6   04   00 a = 1 4 1 4 0 , b = 2     5   65   64 _ _ --> ⇒ ⇒ --> ( 2 a + b ) b = 2828 2 × × --> 2 = 56564 ≤ ≤ --> 60400   38   36 {\displaystyle {\begin{array}{ll}\quad {\color {Red}1}~~{\color {Green}4}.~~{\color {Blue}1}~~{\color {Purple}4}~~{\color {Orange}2}\\{\sqrt {2|00.00|00|00}}\\\quad {\underline {1\quad ~}}&\quad {\color {Red}1}\times {\color {Red}1}\leq 2\\\quad 1~00&a={\color {Red}1}0,b={\color {Green}4}\\\quad {\underline {~~\,96\quad ~}}&\quad \Rightarrow (2a+b)b=2{\color {Green}4}\times {\color {Green}4}=96\leq 100\\\qquad ~4~00&a={\color {Red}1}{\color {Green}4}0,b={\color {Blue}1}\\\qquad ~{\underline {2~81\quad ~}}&\quad \Rightarrow (2a+b)b=28{\color {Blue}1}\times {\color {Blue}1}=281\leq 400\\\qquad ~1~19~00&a={\color {Red}1}{\color {Green}4}{\color {Blue}1}0,b={\color {Purple}4}\\\qquad ~{\underline {1~12~96\quad ~}}&\quad \Rightarrow (2a+b)b=282{\color {Purple}4}\times {\color {Purple}4}=11296\leq 11900\\\qquad \quad ~~6~04~00&a={\color {Red}1}{\color {Green}4}{\color {Blue}1}{\color {Purple}4}0,b={\color {Orange}2}\\\qquad \quad ~~{\underline {5~65~64}}&\quad \Rightarrow (2a+b)b=2828{\color {Orange}2}\times {\color {Orange}2}=56564\leq 60400\\\qquad \quad \quad ~\,38~36\\\end{array}}}

200 ≈ ≈ --> 14.14213562373095048801668872421 {\displaystyle {\sqrt {200}}\approx 14.14213562373095048801668872421}

四舍五入得答案为14.14。

事实上，将算法稍作改动，可以开任何次方的根，详见""n""次方算法。

利用高精度长式除法可以计算出1至20的平方根如下：

牛顿法

如果要求 S ( S > 1 ) {\displaystyle S\,(S>1)} 的平方根，选取 1 < x 0 < S {\displaystyle 1\,

例子：求 125348 {\displaystyle {\sqrt {125348}}} 至6位有效数字。

因此 125348 ≈ ≈ --> 354.045 {\displaystyle {\sqrt {125348}}\approx 354.045} .

连分数

平方根可以简便地用连分数的形式表示，关于连分数请见连分数，其中1至20的算术平方根分别可用连分数表示为：1 = 1 {\displaystyle {\sqrt {1}}=1} 2 {\displaystyle {\sqrt {2}}} =[1;2,2,2,2…]3 {\displaystyle {\sqrt {3}}} =[1;1,2,1,2…]4 {\displaystyle {\sqrt {4}}} =25 {\displaystyle {\sqrt {5}}} =[2;4,4,4,4…]6 {\displaystyle {\sqrt {6}}} =[2;2,4,2,4…]7 {\displaystyle {\sqrt {7}}} =[2;1,1,1,4,1,1,1,4…]8 {\displaystyle {\sqrt {8}}} =[2;1,4,1,4…]9 {\displaystyle {\sqrt {9}}} =31 0 {\displaystyle {\sqrt {1}}0} =[3;6,6,6,6…]1 1 {\displaystyle {\sqrt {1}}1} =[3;3,6,3,6…]1 2 {\displaystyle {\sqrt {1}}2} =[3;2,6,2,6…]1 3 {\displaystyle {\sqrt {1}}3} =[3;1,1,1,1,6,1,1,1,1,6…]1 4 {\displaystyle {\sqrt {1}}4} =[3;1,2,1,6,1,2,1,6…]1 5 {\displaystyle {\sqrt {1}}5} =[3;1,6,1,6…]1 6 {\displaystyle {\sqrt {1}}6} =41 7 {\displaystyle {\sqrt {1}}7} =[4;8,8,8,8…]1 8 {\displaystyle {\sqrt {1}}8} =[4;4,8,4,8…]1 9 {\displaystyle {\sqrt {1}}9} =[4;2,1,3,1,2,8,2,1,3,1,2,8…]2 0 {\displaystyle {\sqrt {2}}0} =[4;2,8,2,8…]

连分数部分均循环，省略号前为2或4个循环节。

巴比伦方法

重复的算术运算

这个方法是从佩尔方程演变过来的，它通过不断减去奇数来求得答案。

尺规作图

问题

给定线段AB和1，求一条长为√AB的线段。

解法

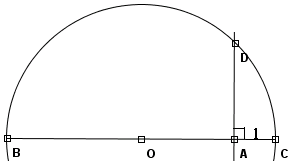
画线AB，延长BA至C使AC=1

以BC的中点为圆心，OC为半径画圆

过A画BC的垂直线，垂直线和圆弧交于D，AD即为所求之长度

证明

将整个过程搬到直角座标上，已知AC=1，设

O=（0,0）

AB=n

直径为BC的圆就是 x 2 + y 2 = ( n + 1 2 ) 2 {\displaystyle x^{2}+y^{2}=\left({\frac {n+1}{2}}\right)^{2}} （圆的方程式： x 2 + y 2 = {\displaystyle x^{2}+y^{2}=} r）（其中,r表示半径。）

将 ( n + 1 2 − − --> 1 ) {\displaystyle \left({\frac {n+1}{2}}-1\right)} （A,D所在的x座标）代入上面的方程式

( n + 1 2 − − --> 1 ) 2 + y 2 = ( n + 1 2 ) 2 {\displaystyle \left({\frac {n+1}{2}}-1\right)^{2}+y^{2}=\left({\frac {n+1}{2}}\right)^{2}}

解方程，得y=√n。

参见

方根

增乘开平方法

二项式定理

牛顿法

参考资料

^劳汉生《珠算与实用算术》ISBN 7-5375-1891-2/O

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。