采样定理-族谱新闻-族谱网

采样定理

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:1162次

转发:0次

评论:0

简介采样是将一个信号（例如时间或空间上连续的函数）转换为数字序列（时间或空间上离散的函数）的过程。这个定理的香农版本陈述为：如果函数x(t)不包含高于Bcps（次/秒）的频率，它完全取决于一系列相隔1/(2B)秒的点的纵坐标。因此2B样本/秒或更高的采样频率就足够了。相反，对于一个给定的采样频率fs，完全重构的频带限制为B≤fs/2。在频带限制过高（或根本没有频带限制）的情形下，重构表现出的缺陷称为混叠。现在对于此定义的陈述有时会很小心的指出x(t)必须不包括频率恰好为B的正弦曲线，或是B必须小于½的采样频率。这二个门槛，2B及fs/2会称为奈奎斯特速率（英语：Nyquistrate）及奈奎斯特频率。这些是x(t)及采样设备的属性。上述的不等式会称为奈奎斯特准则，有时会称为拉贝准则（Raabecondition）。此定理也可以用在其他定义域（例如离散系统）的函数下，唯一的不同是量测t,fs...

简介

采样是将一个信号（例如时间或空间上连续的函数）转换为数字序列（时间或空间上离散的函数）的过程。这个定理的香农版本陈述为：

如果函数 x(t) 不包含高于 B cps（次/秒）的频率，它完全取决于一系列相隔 1/(2 B ) 秒的点的纵坐标。

因此 2 B 样本/秒或更高的采样频率就足够了。相反，对于一个给定的采样频率 f s ，完全重构的频带限制为 B ≤ f s /2。

在频带限制过高（或根本没有频带限制）的情形下，重构表现出的缺陷称为混叠。现在对于此定义的陈述有时会很小心的指出 x ( t )必须不包括频率恰好为 B 的正弦曲线，或是 B 必须小于½的采样频率。这二个门槛，2 B 及 f s /2会称为奈奎斯特速率（英语： Nyquist rate ）及奈奎斯特频率。这些是 x ( t )及采样设备的属性。上述的不等式会称为奈奎斯特准则，有时会称为拉贝准则（Raabe condition）。此定理也可以用在其他定义域（例如离散系统）的函数下，唯一的不同是量测 t , f s 和 B 的单位。

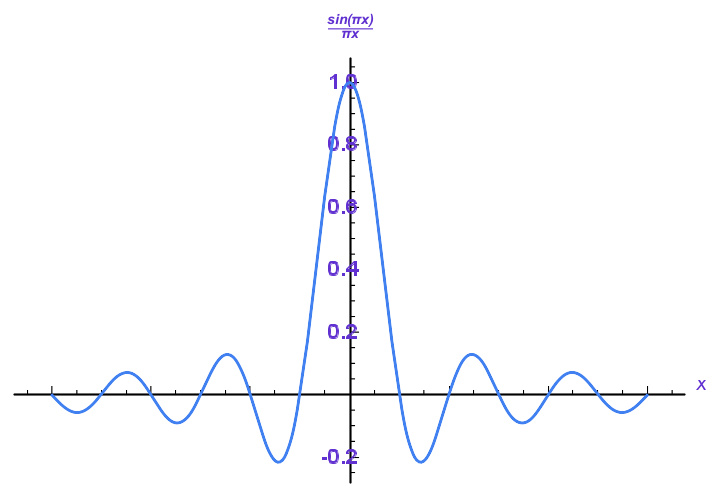
正规化的Sinc函数：sin(π x ) / (π x ) ...其中央峰值在 x = 0，其他整数值的 x 时为零交越点

符号 T = 1/ f s 常用来表示二次采样之间的时间间隔，称为采样周期或是采样区间。函数 x ( t )的采样常用 x [ n ] = x ( nT )表示（较早期的文献会用 x n ），其中 n 为正整数。在数学上理想的采样还原（插值）和Sinc函数有关，每次的采样都用中心点在采样时间 nT ，幅度是采样值 x [ n ]的Sinc函数代替。最后将Sinc函数加总，得到连续的函数。数学上等效的方式是将Sinc函数和一连串的狄拉克δ函数卷积，再依采样到的值来加权。不过这些方式在数学上都是不实际的。不过有些有限长度的函数可以近似Sinc函数，这种因为近似的不完美造成的误差称为插值误差（interpolation error）。

实际的数字模拟变换器既不会产生加权而有延迟的Sinc函数，也不会产生理想的狄拉克δ函数，若是其模拟重建是用零阶保持（英语： Zero-order hold ），其输出的是由不同幅度及有延迟的矩形函数组成的阶跃函数，一般后面会有抗镜像滤波器（anti-imaging filter）来清除假的高频成分。

混叠

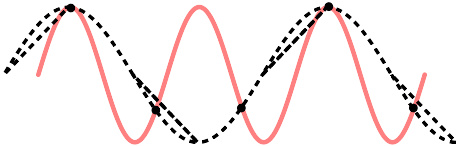
二个正弦波的频率不同，但其采样值相关，其中至少有一个的频率超过采样频率的一半

如果不能满足上述采样条件，采样后信号的频率就会重叠，即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号。这种频谱的重叠导致的失真称为混叠，而重建出来的信号称为原信号的混叠替身，因为这两个信号有同样的样本值。

若 x ( t )为一函数，其傅里叶变换 X ( f )为:

泊松求和公式（英语： Poisson summation formula ）指出 x ( t )的采样 x ( nT )已以产生 X ( f )的周期和（英语： periodic summation ），结果为：

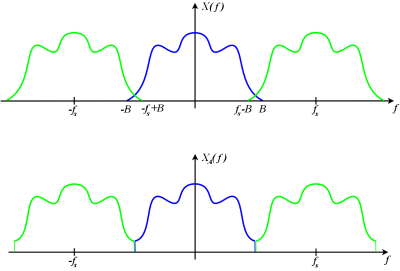
图4： X ( f )（上图蓝色部分）及 X A ( f )（下图蓝色部分）是二个不同函数 x ( t )及 x A ( t )（原函数省略不列出）的连续傅里叶变换。当二个函数以 f s 的速率采样时，且确认信号的离散傅里叶变换（DTFT）时，其镜相（image，绿色部分）会和变换后信号（蓝色部分）叠加。在这个假设的例子中，二函数的离散傅里叶变换相同，表示采样到的信号也相同，可是在采样前的原函数是不同的。若这是声音频号， x ( t )和 x A ( t )听起来是不一样的，可是其以 f s 速率的采样是一样的，因此最后重制的声音是相同的， x A ( t )是 x ( t )在此采样频率下的混叠（alias）

是一个周期函数，等效为傅里叶级数，系数为 T • x ( nT )。此函数也称为数列 T • x ( nT )的离散时间傅里叶变换(DTFT)，n为整数。

如图4所示， X ( f ) 的拷贝被平移了 f s 的倍数，并相加合并。对于一个带限函数（对所有 | f | ≥ B ， X ( f ) = 0 ），在 f s 足够大的时候，这些拷贝之间仍然分得清楚。但如果奈奎斯特准则并不满足，相邻部分就会重叠，一般就不能明确辨别出 X ( f )。任何超过 f s /2 的频率分量都会与较低的频率分量难以区分，称作与其中一个拷贝发生“混叠”。在这种情况下，通常的插值法就会产生混叠，而不是原始的分量了。

以下两种措施可避免混叠的发生：

提高采样频率，使之达到最高信号频率的两倍以上；

引入低通滤波器或提高低通滤波器的参数；该低通滤波器通常称为抗混叠滤波器

当采样率预先由其他因素（如行业标准）确定的时候， x ( t ) 通常要先滤波以将高频分量减少到可以接受的水平，再进行采样。所需的滤波器的种类为低通滤波器，而在这种应用中叫做抗混叠滤波器。抗混叠滤波器可限制信号的带宽，使之满足采样定理的条件。这在理论上是可行的，但是在实际情况中不可能做到。因为滤波器不可能完全滤除奈奎斯特频率之上的信号，所以，采样定理要求的带宽之外总有一些“小的”能量。不过抗混叠滤波器可使这些能量足够小，以至可忽略不计。

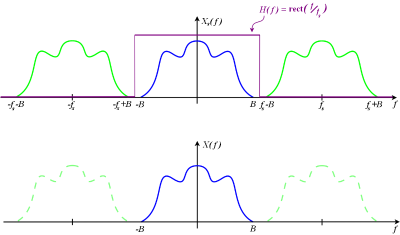
图5： X s ( f )是由适当带宽滤波器滤波后的信号，其频谱（蓝色）和其相邻的DTFT镜像（绿色）不会重叠。brick-wall低通滤波器 H ( f )可以移除镜像，留下原始的频谱 X ( f )，由采样后的信号还原为（滤波后）的原始信号

由泊松求和的特例来推导

从图5中可以看到，若 X ( f )的复本（也称为镜像）之间没有和 k = 0的项重叠，可以由 X s ( f )用以下的乘积来还原：

此时证明了采样定理，因此 X ( f )可以确定 x ( t )，而且只有唯一解。

剩下的就只有推导重构的公式。 H ( f )不需在 [ B , f s − B ] 的区域有准确的定义，因为 X s ( f )在此区域为零。不过最坏的情形是 B = f s /2，奈奎斯特频率。一个在此情形及其他较轻微的条件下都适用的函数为：

其中rect(•)为矩形函数，因此：

等式二侧反变换，可以得到惠特克-香农插值公式（英语： Whittaker–Shannon interpolation formula ）

上式就是用采样值 x ( nT )来重构 x ( t )的方式。

若 f s 大于所需值，也就是 T 较小，称为过采样（oversampling），由图5可以看出过采样对重构信号没有任何效果，但可以提供一块“转态区”，此区域内的 H ( f )可以是一些非零的值。相反的，欠采样（英语： Undersampling ）会造成混叠，一般而言无法重构原始信号。

理论上，插值公式可以用低通滤波器来实现，其冲激响应为sinc( t / T )，输入为 ∑ ∑ --> n = − − --> ∞ ∞ --> ∞ ∞ --> x ( n T ) ⋅ ⋅ --> δ δ --> ( t − − --> n T ) , {\displaystyle \textstyle \sum _{n=-\infty }^{\infty }x(nT)\cdot \delta (t-nT),} ，即为一个被采样信号调制过的脉冲序列（英语： Dirac comb ）函数。实际的数字模拟变换器（DAC）会用零阶保持器（英语： zero-order hold ）来近似，此时过采样可以减少近似的误差。

香农的原始证明

泊松证明了 Eq.1 中的傅里叶级数会产生 X ( f ) 的周期求和，不管 f s 和 B 是什么值。然而香农只推导了 f s = 2B 情形下级数的系数。几乎引用了香农原始的论文：

香农对于此定理的证明已经完成了，不过香农进一步探讨用Sinc函数重构原函数，也就是今日的惠特克–香农内插公式（英语： Whittaker–Shannon interpolation formula ），他没有推导或是证明sinc函数的性质，但这些对于当时阅读其作品的工程师不会觉得陌生，因为当时已经知道矩形函数和Sinc函数的傅里叶对关系。

和其他证明类似，此处假设原函数的傅里叶变换存在，因此证明中没有说明采样定理是否可以延伸到有限带宽的固定随机过程。

脚注

在多变数信号及图形上的应用

图6：采样不足的图，会出现莫列波纹

图7

采样定理常表示为单一变数的函数，因此定理可以直接应用到和时间相关的一维信号。不过采样定理可以直接延伸到任意数量变数的函数。例如像灰阶影像常表示为二维的实数阵列（或是矩阵），其中的实数表示在对应行及列的采样位置下，像素的相对强度。因此图案会需要二个独立的变数来表示其位置，一个表示对应的行，一个表示对应的列。

彩色影像一般会包括三个独立的灰阶值，分别表示红色、绿色及蓝色等三原色（三原色光模式，简称RGB）的强度。其他用三个元素的向量表示一个点的颜色空间有HSL和HSV色彩空间、CIELAB及XYZ等。而像CMYK则是用浅蓝色、紫红色、黄色及黑色的强度来表示。这些色彩空间都是二维空间上的向量值函数（英语： vector-valued function ）。

和一维离散信号的情形类似，若图形的采様清晰度（或是像素密度）不适当，可能会有混叠的情形。例如密条纹衬衫若是用的数值若是用数码相机的图像传感器采样时，可能会造成混叠，这种二维的混叠会形成莫列波纹，改善方式是提高空间的采样率，例如拍照时更靠近衬衫，用高清晰度的感测器，或是在采样前先进行光学模糊处理。

另一个例子是右边的方格条纹，上方的图是不满足采样定理下的信号。下方则是先经过低通滤波器再降采样，得到一个较小，但没有莫列波纹。上图则是直接降采样，没有先经过低通处理后的图。

采样定理在影像上的应用需小心的进行。例如相机中标准影像感测器（CCD或CMOS）的采样程序和理想的采样程序有相当的差距，理想的采样程序会在一个点量测其影像强度，但影像感测器中为了获得足够的光量，其感测影像的区域较。换句话说，感测器是一个有限宽度的点扩散函数。一般而言这类感测器采样到的模拟光学信息不是有限带宽的，而不理想的采样本身即为低通滤波器，不过不一定可以移除会造成混叠的高频噪声。若采样区域（感测器大小）没有大到可以有反锯齿效果时，一般会需要独立的反锯齿滤镜（光学低通滤镜）来使影像模糊。虽然影像有这些和采样定理有关的问题，不过采样定理可以描述提升采样及减采样的基础。

图8：一组在临界频率的弦波，采様时都是反复出现的+1和–1，他们都是彼此的混叠信号，甚至其频率还没超过采样频率的一半

临界频率

为了描述 f s > 2 B 的必要性，考虑右图（图8）中的一组弦波，公式如下，但θ值各有不同：

其中 f s = 2 B 或是可以写为 T = 1/(2 B )，采样值为：

和θ值无关。上述的歧义是采样定理中使用严格的不等式，不允许等式的原因。

对于非基带信号的采样

香农曾提到：

因此这是一个针对没有基带成分信号（其频带有一部分的信号非零，但此宽度又和最大频率无关）进行采样的充份条件。

带通条件为 X ( f ) = 0，针对在所有在开区域范围以外的非负 f ：

针对某非负整数 N 。此公式包括一般的基带条件， N =0。

对应的内插函数为理想Sinc带通滤波器的冲激响应，（而不是之前用的理想Sinc低通滤波器），会切掉频带的上方及下方，这也是一组低通滤波器冲激响应的差：

其他的推广，例如信号在数个不连续的频带，也是可行的。甚至是最广义的采样定理也不一定有一个可能正确的反例。也就是说无法确定是否只要不满足采样定理，就一定会有信号的丧失。不过以工程的角度来看，比较保守的作法是假设若不满足采样定理，就很可能会有信号的丧失。

非均匀采样

香农的采样定理可以延伸到非均匀采样（英语： nonuniform sampling ），也就是采样的时间间隔非一定值。非均匀采样的采样定理指出针对band-limited的信号，只要平均采样频率满足奈奎斯特条件，就可以从采样信号完整重建原始信号。因此虽然均匀采样在信号重建的算法上比较简单，但这不是完整重建的必要条件。

非基带及非均匀采样的泛用理论是在1967年由亨利·蓝道提出。简单的说，蓝道证明了平均采样率至少需要是信号占据带宽的二倍，但前提是已知信号的频谱及其占据的带宽。在1990年代末期，此研究已延伸到信号占据带宽的数量已知，但实际在频谱上位置未知的情形。在2000年代已利用压缩感知发展了一个完整的理论。此理论用信号处理的语言写成，在2009年的论文中发表。论文中证明，若频率的位置未知，则采样频率需至少为奈奎斯特准则的二倍。换句话说，因为不知道光学频谱的位置，需要将采样频率乘二为代价。注意此最小采样频率的要求不一定保证其数值稳定性。

欠采样

当一个信号被欠采样（英语： Undersampling ）时，必须满足采样定理以避免混叠。为了满足采样定理的要求，信号在进行减采样操作前，必须通过一个具有适当截止频率的低通滤波器。这个用于避免混叠的低通滤波器，称为抗混叠滤波器。

在奈奎斯特速率以下，有额外限制条件的采样

奈奎斯特–香农采样定理是对于带限函数采样及重建的充分条件。若是用惠特克–香农内插公式（英语： Whittaker–Shannon interpolation formula ）重建原信号，奈奎斯特准则也是避免混叠的必要条件，因为若采様速率小于信号频带限制的二倍，可能有些信号无法正确重建。不过若信号有其他的限制，则奈奎斯特准则就不是混叠的必要条件了。

像近来在进行研究的压缩感知就是一个利用对信号额外假设来进行压缩的例子，压缩感知可以用奈奎斯特速率要慢的速率采样，然后可以完整的重建原信号。这特别用在信号在一些层面较稀疏（或可压缩）的情形。像压缩感知可以处理有效带宽（EB)）很低，但不确定其频率分布位置的信号（此时采样定理就不适用了）。换句话说，其频谱较稀疏。若用采样定理，最小的采样速率是2 B ，若是用压缩感知，采样速率若略低于2EB，仍可以完整的重建。不过此作法的重建已不再是用公式处理，而是要求解凸优化，需要有良好研究，而可能是非线性的方式处理。