单散射和多重散射

假若辐射只被一个局部性散射体散射，则称此为单散射。假若许多散射体集中在一起，辐射可能会被散射很多次，称此为多重散射。单散射可以被视为一个随机现象；而多重散射通常是比较命定性的。这是两种散射的主要不同点。

由于单独的散射体的位置，相对于辐射路径，通常不会明确的知道。所以，散射结果强烈地依赖于入射轨道参数。对于观测者，散射结果显得相当的随机。移动电子朝着原子核碰撞是一个标准案例。由于不确定性原理，相对于电子的入射路径，原子的确定位置是个未知数，无法准确地测量出来，碰撞后，电子的散射行为是随机的。所以，单散射时常用概率分布来描述

在多重散射过程里，经过众多的散射事件，散射作用的随机性很容易会因为平均化而被凐灭不见，辐射的最终路径会显示为强度的命定性（deterministic）分布。光束穿过浓厚大雾是一个标准案例。多重散射可以与扩散类比。在许多状况，两个术语可以替代使用。用来制造多重散射的光学器材，称为扩散器。

不是每一种单散射都是随机地。一个完美控制的激光束能够准确地散射于一个微粒，产生出命定性的结果。这样的状况也会发生于雷达散射，目标大多数是宏观物体，像飞机或火箭。

类似地，多重散射有时也会产生很随机的结果，特别是相干辐射。当相干辐射被多重散射的时候，强度会发生随机涨落，称此现象为散斑（speckle）。假若，一个相干辐射的不同部分散射于不同的散射体，则也会产生散斑。在某些罕见的状况，多重散射的散射次数并不多，随机性并没有被平均化凐灭。学术界公认，这类系统很不容易精确地模型化。

散射的主要研究问题，时常涉及到预测各种系统怎样散射辐射。给予足够的计算资源和系统信息，这些问题大都可以解析。一个广泛研究，更加困难的挑战是逆散射问题（inverse scattering problem）。这问题主要研究的是，从观测到的散射行为，来决定入射辐射或散射体的性质。一般而言，解答不是唯一的；不同的散射体可以给予同样的散射样式。幸运地，科学家找到一些方法，来萃取许多关于散射体的资料。虽然这些资料并不完全，但还是相当有用。这些方法广泛的用于感测和计量学（metrology）。

许多科技领域显著地应用到散射和散射理论。例如，雷达感测、超声波检查、半导体芯片检验、聚合过程监视、电脑成像等等。

电磁散射

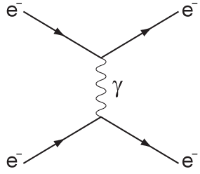
两个电子，经由一个虚光子的发射，而产生的散射，可以由费曼图展示出来。

电磁波是一种最为人熟知，最常碰到的辐射形式。其中，光波散射是不可避免的日常现象。无线电波散射则乃雷达科技的核心物理机制。因为某些方面的不同，电磁波散射可以清楚地分支为不同的领域，各自有各自的取名。弹性散射（涉及极微小的能量转移）主要有瑞利散射和米氏散射。非弹性散射包括布里渊散射（Brillouin scattering）、拉曼散射、非弹性X-光散射、康普顿散射等等。

大多数物体都可以被看见，主要是因为两个物理过程：光波散射和光波吸收。有些物体几乎散射了所有入射光波，这造成了物体的白色外表。光波散射也可以给予物体颜色。例如，不同色调的蓝色，像天空的天蓝、眼睛的虹膜、鸟的羽毛等等。奈米粒子的共振光波散射会产生不同的高度饱和的，生动的色相，特别是当涉及表面等离子体共振（surface plasmon resonance）。

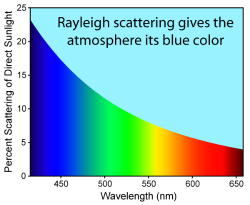
在瑞利散射里，电磁辐射（包括光波）被一个小圆球散射。圆球可能是一个粒子、泡沫、水珠、或甚至于密度涨落。物理学家瑞利勋爵最先发现这散射效应的正确模型，因此称为瑞利散射。为了要符合瑞利模型的要求，圆球的直径必须超小于入射波的波长，通常上界大约是波长的1/10。在这个尺寸范围内，散射体的形状细节并不重要，通常可以视为一个同体积的圆球。当阳光入射于大气层时，气体分子对于阳光的瑞利散射，使得天空呈现蓝色。这是根据瑞利著名的方程：

其中，I{\displaystyle I\,\!}是强度，λ λ -->{\displaystyle \lambda \,\!}是波长。

阳光的蓝色光波部分波长比较短，散射强度比较大；而红色光波部分波长比较长，散射强度比较小。外太空的辐射通过地球大气层时，衰减的主要原因是辐射吸收和瑞利散射。散射的程度变化是粒子直径与波长比例的函数，连同许多其它因子，像极化、角度、以及相干性等等。

瑞利散射不适用于直径较大的散射体。德国物理学家古斯塔夫·米最先找到这问题的解答。因此，大于瑞利尺寸的圆球的散射被称为米氏散射。在米氏区域内，散射体的形状变的很重要。这理论只能用在类球体。

瑞利散射和米氏散射都可以被视为弹性散射，光波的能量并没有大幅度地改变。可是，移动的散射体所散射的电磁波会产生多普勒效应，能量会稍微改变。这效应可以被用来侦测和测量散射体的速度，可以应用于光达（LIDAR）和雷达这一类科技仪器。

当粒子直径与波长比例大于10的时候，几何光学的定律可以用来描述光波与粒子的相互作用。在这里，通常不称这相互作用为散射。

对于一些瑞利模型和米式模型不适用的案例，像不规则形状粒子，有很多种不同的数值计算方法可以让我们选择使用，求算散射的解答。最常见的方法是有限元方法。此法解析麦克斯韦方程组，寻求散射的电磁场的分布。程式工程师特别设计出复杂的软件，专门计算这类问题。只需要使用者给出散射体的折射率或折射率函数，电脑就可以计算出电磁场结构的二维或三维模型。假若结构比较庞大复杂，则可能需要高功能电脑大量的运算时间，才能得到结果。

另外一种特别的电磁散射是相干回散射（backscatter）。这是一个相当不为人知的现象。当相干辐射（像激光光束）传播通过一个拥有很多散射体的介质时，电磁波会被散射很多次。一个代表性的多重散射介质例子是浓厚云块。朝着原本入射方向的反方向，相干回散射效应会产生一个非常大的峰值强度。实际上，一般的电磁波很大部分都会散射回去。对于非相干辐射，散射通常会在反方向产生一个局部最大值。可是，相干辐射的峰值强度是非相干辐射的两倍。测量这些数值是很困难的。原因有两个。第一个原因是，直接地测量回散射同时也会阻挡入射电磁波。但是，科学家已经想出精巧的方法来克服这问题。第二个原因是，强度峰通常会是非常的尖锐。侦测器必须拥有非常高的角分辨率，才能够看到峰值，不会将强度峰值与邻近的低强度值平均起来。

参阅

廷得耳效应

X射线晶体学

布拉格散射

卢瑟福散射

汤姆孙散射

中子散射（neutron scattering）

小角散射（small-angle scattering）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。