历史

奥里斯姆

ζ函数最早出现于1350年左右，当时的尼克尔·奥里斯姆发现了调和级数发散，即ζ ζ -->(1)=1+12+13+14+...→ → -->∞ ∞ -->{\displaystyle \zeta (1)=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+...\to \infty }

欧拉

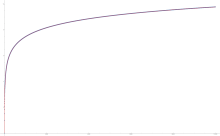
第n个调和数（蓝点）与Log(n)+γ(红线)的图像

之后的一次进展来自莱昂哈德·欧拉，他给出了调和级数呈对数发散。

除此之外，他还在1735年给出了巴塞尔问题的解答，得到ζ ζ -->(2)=π π -->26{\displaystyle \zeta (2)={\frac {\pi ^{2}}{6}}} 的结果。欧拉最初的证明可以在巴塞尔问题中看到，然而那是他的第一个证明，因而广为人知。 事实上，那个证明虽有不严谨之处，但是欧拉仍然有自己的严格证明。

欧拉在1737年还发现了欧拉乘积公式：∑ ∑ -->n=1∞ ∞ -->1ns=∏ ∏ -->p(1− − -->1ps)− − -->1{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p}(1-{\frac {1}{p^{s}}})^{-1}} 这是ζ函数与素数的联黎曼朦胧征兆，其证明可以在证明黎曼ζ函数的欧拉乘积公式中看到。 通过这条公式，容易证明当 Re⁡ ⁡ -->(s)>1{\displaystyle {\begin{smallmatrix}\operatorname {Re} (s)>1\end{smallmatrix}}} 时，ζ ζ -->(s)>0{\displaystyle {\begin{smallmatrix}\zeta (s)>0\end{smallmatrix}}} 1749年，欧拉通过大胆的计算发现了ζ ζ -->(− − -->1)=1+2+3+4+5+...=− − -->112{\displaystyle \zeta (-1)=1+2+3+4+5+...=-{\frac {1}{12}}}ζ ζ -->(− − -->2)=12+22+32+42+52+...=0{\displaystyle \zeta (-2)=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+...=0}ζ ζ -->(− − -->3)=13+23+33+43+53+...=1120{\displaystyle \zeta (-3)=1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+...={\frac {1}{120}}} 发现ζ(s)与ζ(1-s)之间存在某些关系。

黎曼

波恩哈德·黎曼对ζ解析延拓，用于素数的分布理论

将欧拉所做的一切牢牢地置于坚石之上的是黎曼，他在1859年的论文论小于给定数值的素数个数（英语：On_the_Number_of_Primes_Less_Than_a_Given_Magnitude）以及未发表的手稿中做出了多项进展：

第一积分表示： ζ ζ -->(s)=1Γ Γ -->(s)∫ ∫ -->0∞ ∞ -->xs− − -->1ex− − -->1dx{\displaystyle \zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} x}

完备化的ζ，即黎曼ξ函数： ξ ξ -->(s)=π π -->− − -->s2Γ Γ -->(s2)ζ ζ -->(s){\displaystyle \xi (s)=\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)} ，满足函数方程 ξ ξ -->(s)=ξ ξ -->(1− − -->s){\displaystyle \xi (s)=\xi (1-s)}

第二积分表示： φ φ -->(x)=∑ ∑ -->n=1∞ ∞ -->e− − -->π π -->n2x{\displaystyle \varphi (x)=\sum _{n=1}^{\infty }e^{-\pi n^{2}x}} ，则 ξ ξ -->(s)=∫ ∫ -->0∞ ∞ -->φ φ -->(x)xs2− − -->1dx{\displaystyle \xi (s)=\int _{0}^{\infty }\varphi (x)x^{{\frac {s}{2}}-1}\,\mathrm {d} x}

黎曼 - 冯·曼戈尔特公式（英语：Riemann–von Mangoldt formula）：以0(T){\displaystyle {\begin{smallmatrix}0 表示虚部介于0与T之间的非平凡零点数量，则 N(T)=T2π π -->log⁡ ⁡ -->T2π π -->− − -->T2π π -->+O(log⁡ ⁡ -->T){\displaystyle N(T)={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+\mathrm {O} (\log T)}

黎曼猜想：ζ函数的所有非平凡零点的实部非常有可能均为12{\displaystyle {\begin{smallmatrix}{\frac {1}{2}}\end{smallmatrix}}}

第三积分表示： ζ ζ -->(s)=12π π -->iΓ Γ -->(1− − -->s)∮γ γ -->zs− − -->1ez1− − -->ezdz{\displaystyle \zeta (s)={\frac {1}{2\pi i}}\Gamma (1-s)\oint _{\gamma }{\frac {{z^{s-1}}{e^{z}}}{1-{e^{z}}}}\,\mathrm {d} z} ，其中围道γ逆时针环绕负实轴

第三积分表示的围道γ

黎曼-西格尔公式（英语：Riemann–Siegel formula）：给出计算ξ函数的数值的方法

零点的计算：计算了虚部介于0与100的所有零点的数值

素数的分布公式：引入黎曼素数计数函数，给出了它与ζ函数的关系

阿达马与普森

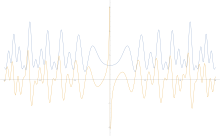
ζ(1+it)的图像，蓝色为实部，黄色为虚部

1896年，雅克·阿达马与普森几乎同时地证明了ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}的所有非平凡零点的实部均小于1，即Re⁡ ⁡ -->(s)=1{\displaystyle {\begin{smallmatrix}\operatorname {Re} (s)=1\end{smallmatrix}}}上无非平凡零点，从而完成了素数定理的证明。

希尔伯特

1900年，希尔伯特在巴黎的第二届国际数学家大会上作了题为《数学问题》的演讲，提出了23道最重要的数学问题，黎曼假设在其中作为第8题出现。 之后，希尔伯特提出了希尔伯特－波利亚猜想，具体时间及场合未知。

玻尔与兰道

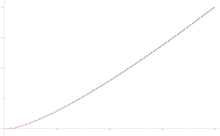
虚部介于0与T的零点数量（蓝点）与黎曼-冯·曼格尔特公式（红线）的图像

1914年，哈那德·玻尔和爱德蒙·兰道证明了玻尔-兰道定理：含有临界线的任意带状区域都几乎包含了ζ的所有非平凡零点，表明了临界线为零点汇聚的“中心位置”。

哈代与李特尔伍德

1921年，哈代和李特尔伍德证明了存在常数T，使临界线上虚部位于0与T之间的非平凡零点的数量至少为KT{\displaystyle {\begin{smallmatrix}KT\end{smallmatrix}}}。

塞尔伯格

1942年，阿特勒·塞尔伯格更进一步，证明了存在常数T，使临界线上虚部位于0与T之间的非平凡零点的数量至少为KTlog⁡ ⁡ -->T{\displaystyle {\begin{smallmatrix}KT\log T\end{smallmatrix}}}，这意味着ζ函数在临界线上的非平凡零点在所有零点中占有一个正密度，而临界线Re⁡ ⁡ -->(s)=12{\displaystyle {\begin{smallmatrix}\operatorname {Re} (s)={\frac {1}{2}}\end{smallmatrix}}}对于临界带0(s)<1{\displaystyle {\begin{smallmatrix}0 的测度为0。

解析延拓

对ζ函数解析延拓时使用的围道

ζ函数原本定义在右半平面Re⁡ ⁡ -->s>1{\displaystyle {\begin{smallmatrix}\operatorname {Re} s>1\end{smallmatrix}}}上，并且在此区域内为全纯函数

解析延拓后在全局具有积分表达式

满足函数方程

特别地，如果考虑正规化的ζ，即黎曼ξ函数

那么它满足函数方程

和数论函数的关系

黎曼ζ函数可看做是具有如下形式的级数的一个特例：

这种类型的级数被称作狄利克雷级数。当f为狄利克雷特征时，又称作狄利克雷L函数，也有与黎曼猜想相应的广义黎曼猜想

为了方便对数论函数作讨论，此处引入狄利克雷卷积f∗ ∗ -->g{\displaystyle {\begin{smallmatrix}f*g\end{smallmatrix}}}：(f∗ ∗ -->g)(n)=∑ ∑ -->pq=nf(p)g(q){\displaystyle (f*g)(n)=\sum _{{\text{pq}}=n}f(p)g(q)}

设 F⁡ ⁡ -->(s)=∑ ∑ -->n=1∞ ∞ -->f(n)ns{\displaystyle \operatorname {F} (s)=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}} ， G⁡ ⁡ -->(s)=∑ ∑ -->n=1∞ ∞ -->g(n)ns{\displaystyle \operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}} 于是显然 F⁡ ⁡ -->(s)G⁡ ⁡ -->(s)=∑ ∑ -->n=1∞ ∞ -->(f∗ ∗ -->g)(n)ns{\displaystyle \operatorname {F} (s)\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {(f*g)(n)}{n^{s}}}}

于是，如果数论函数h=1∗ ∗ -->g{\displaystyle {\begin{smallmatrix}h=1*g\end{smallmatrix}}}，亦即 h(n)=∑ ∑ -->d∥ ∥ -->ng(d){\displaystyle h(n)=\sum _{d\|n}g(d)} (此时，h(n){\displaystyle {\begin{smallmatrix}h(n)\end{smallmatrix}}}与g(d){\displaystyle {\begin{smallmatrix}g(d)\end{smallmatrix}}}可通过默比乌斯反演公式相互转换) 那么 H⁡ ⁡ -->(s)=∑ ∑ -->n=1∞ ∞ -->h(n)ns=ζ ζ -->(s)∑ ∑ -->n=1∞ ∞ -->g(n)ns{\displaystyle \operatorname {H} (s)=\sum _{n=1}^{\infty }{\frac {h(n)}{n^{s}}}=\zeta (s)\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}} 通常两侧的求和有一个是相对简单的函数，或是和ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}直接相关的函数 如果对g(n){\displaystyle {\begin{smallmatrix}g(n)\end{smallmatrix}}}的求和较简单，可以将h(n){\displaystyle {\begin{smallmatrix}h(n)\end{smallmatrix}}}与ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}相联系，反之可以将g(n){\displaystyle {\begin{smallmatrix}g(n)\end{smallmatrix}}}与ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}相联系 即 ∑ ∑ -->n=1∞ ∞ -->g(n)ns=H⁡ ⁡ -->(s)ζ ζ -->(s){\displaystyle \sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}={\frac {\operatorname {H} (s)}{\zeta (s)}}} ， 如下表所示：

佩龙公式

ζ函数与数论函数存在的联系可以通过佩龙公式转化为它和数论函数的求和的关系：设

则由佩龙公式，

其中右上角的"表示如果x是整数，那么求和的最后一项要乘以12{\displaystyle {\begin{smallmatrix}{\frac {1}{2}}\end{smallmatrix}}}。 这样做的其中一个结果就是ζ函数和素数分布的关系。

和素数的关系

欧拉乘积

此函数和素数的关系已由欧拉所揭示：

这是一个延展到所有的素数p的无穷乘积，被称为欧拉乘积。这是几何级数的公式和算术基本定理的一个结果。 如果对上式取对数，则可得到

更进一步的联系

黎曼阶梯素数计数函数

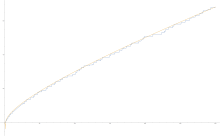
黎曼素数计数函数（蓝色）J(x)与对数积分（金色）Li(x)的图像，x<300

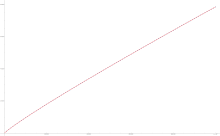
黎曼素数计数函数（蓝点）J(x)与对数积分（红线）Li(x)的图像，x<1 000 000

可以使用黎曼素数计数函数J⁡ ⁡ -->(x){\displaystyle {\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}}建立ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}与素数分布的进一步联系，这也是黎曼在他的论文论小于给定数值的素数个数（英语：On_the_Number_of_Primes_Less_Than_a_Given_Magnitude）中使用的函数，定义如下：

其中κ κ -->(n)={1kn=pk0otherwise{\displaystyle \kappa (n)={\begin{cases}{\frac {1}{k}}&n=p^{k}\\0&\mathrm {otherwise} \end{cases}}} 那么可以建立J⁡ ⁡ -->(x){\displaystyle {\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}}与ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}的零点ρ的联系，称为黎曼显式公式（英语：Explicit formulae (L-function)）

而J⁡ ⁡ -->(x){\displaystyle {\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}}与π π -->(x){\displaystyle {\begin{smallmatrix}\pi (x)\end{smallmatrix}}}的联系可以通过莫比乌斯反演公式完成。π π -->(x)=∑ ∑ -->n=1∞ ∞ -->μ μ -->(n)nJ⁡ ⁡ -->(x)=J⁡ ⁡ -->(x)+O(xlog⁡ ⁡ -->log⁡ ⁡ -->x){\displaystyle \pi (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {J} (x)=\operatorname {J} (x)+\mathrm {O} ({\sqrt {x}}\log \log x)} 然而J⁡ ⁡ -->(x){\displaystyle {\begin{smallmatrix}\operatorname {J} (切比雪夫nd{smallmatrix}}}的表达式过于复杂，如下的切比雪夫函数（英语：Chebyshev function）更为常用。

切比雪夫函数

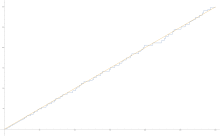
第二切比雪夫函数（蓝线）ψ(x)与y=x（金线）的图像,x<300

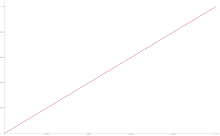
第二切比雪夫函数（蓝点）ψ(x)与y=x（红线）的图像,x<1 000 000

第一切比雪夫函数ϑ ϑ -->(x){\displaystyle {\begin{smallmatrix}\vartheta (x)\end{smallmatrix}}}定义为

而更常用的第二切比雪夫函数ψ ψ -->(x){\displaystyle {\begin{smallmatrix}\psi (x)\end{smallmatrix}}}定义为

其中，如前文定义的 Λ Λ -->(n)={log⁡ ⁡ -->(p)n=pk0otherwise{\displaystyle \Lambda (n)={\begin{cases}\log(p)&n=p^{k}\\0&\mathrm {otherwise} \end{cases}}} 第二切比雪夫函数与第一切比雪夫函数的关系，可看做“等同于”黎曼素数计数函数与素数计数函数的关系。 第二切比雪夫函数ψ ψ -->(x){\displaystyle {\begin{smallmatrix}\psi (x)\end{smallmatrix}}}与ζ ζ -->(s){\displaystyle {\begin{smallmatrix}\zeta (s)\end{smallmatrix}}}的零点ρ有如下的联系

而ψ ψ -->(x){\displaystyle {\begin{smallmatrix}\psi (x)\end{smallmatrix}}}与J⁡ ⁡ -->(x){\displaystyle {\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}}的联系可以通过阿贝尔求和公式（英语：Abel"s_summation_formula）：

其中κ如前文所定义，则由阿贝尔求和公式

零点

解析延拓之后的ζ函数具有零点，他们分别是分布有序的平凡零点（所有负偶数），以及临界带0s(T){\displaystyle {\begin{smallmatrix}\operatorname {N} (T)\end{smallmatrix}}}表示虚部介于0与T之间的非平凡零点数量，则0(T){\displaystyle {\begin{smallmatrix}0 遵循黎曼 - 冯·曼戈尔特公式（英语：Riemann–von Mangoldt formula）：N(T)=T2π π -->log⁡ ⁡ -->T2π π -->− − -->T2π π -->+O(log⁡ ⁡ -->T){\displaystyle N(T)={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+\mathrm {O} (\log T)}。

函数值

黎曼函数在s > 1的情况

ζ函数满足如下函数方程：

对于所有C\{0,1}中的s成立。这里，Γ表示Γ函数。这个公式原来用来构造解析连续性。在s = 1，ζ函数有一个简单极点其留数为1。上述方程中有sin函数，sin⁡ ⁡ -->(π π -->s2){\displaystyle \sin \left({\frac {\pi s}{2}}\right)}的零点为偶数s = 2n，这些位置是可能的零点，但s为正偶数时，sin⁡ ⁡ -->(π π -->s2)Γ Γ -->(1− − -->s){\displaystyle \sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)}为不为零的规则函数（英语：Regular function），只有s为负偶数时，ζ函数才有零点，称为平凡零点。

当s为正整数

欧拉计算出ζ（2k），对于偶整数2k，使用公式

其中B2k是伯努利数。从这个，我们可以看到ζ(2)= π/6, ζ(4) = π/90, ζ(6) = π/945等等。（OEIS中的序列A046988/A002432）。这些给出了著名的π的无穷级数。奇整数的情况没有这么简单。拉马努金在这上面做了很多了不起的工作。 s{\displaystyle s\,}为正偶数时的函数值公式已经由欧拉计算出。但当s{\displaystyle s\,}为正奇数时，尚未找到封闭式。

s趋近于1

其中γ是欧拉-马歇罗尼常数=0.577215...{\displaystyle 0.577215...}

负整数

同样由欧拉发现，ζ函数在负整数点的值是有理数，这在模形式中发挥着重要作用，而且ζ函数在负偶整数点的值为零。

事实上

Bn是白努利数。

因为 B2n+1 =0，故ζ函数在负偶整数点的值为零。

复数值

幅角

函数值表

临界线上的数值计算

临界线上的数值计算可以通过黎曼-西格尔公式（英语：Riemann–Siegel formula）完成。 与之相关的，林德勒夫猜想（英语：Lindelöf hypothesis）：对于任意给定的实数ϵ ϵ -->>0{\displaystyle {\begin{smallmatrix}\epsilon >0\end{smallmatrix}}}，

相关条目

黎曼猜想

狄利克雷级数

狄利克雷卷积

黎曼ξ函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。