历史

第一次提到常数e{\displaystyle e}，是约翰·纳皮尔于1618年出版的对数著作附录中的一张表。但它没有记录这常数，只有由它为底计算出的一张自然对数列表，通常认为是由威廉·奥特雷德制作。第一次把e看为常数的是雅各布·伯努利，他尝试计算下式的值：

已知的第一次用到常数e{\displaystyle e}，是莱布尼茨于1690年和1691年给惠更斯的通信，以b表示。1727年欧拉开始用e{\displaystyle e}来表示这常数；而e{\displaystyle e}第一次在出版物用到，是1736年欧拉的《力学》（Mechanica）。虽然往后年日有研究者用字母c表示，但e{\displaystyle e}较常用，终于成为标准。

用e表示的确实原因不明，但可能因为e{\displaystyle e}是“指数”（exponential）一字的首字母。另一看法则称a，b，c和d有其他经常用途，而e{\displaystyle e}是第一个可用字母。

定义

就像圆周率 π π --> {\displaystyle {\begin{smallmatrix}\pi \end{smallmatrix}}}和虚数单位 i，e{\displaystyle {\begin{smallmatrix}e\end{smallmatrix}}} 是数学中最重要的常数之一。它有几种等价定义，下面列出一部分。

最常见的四种 e 的定义如下：

这些定义可证明是等价的，请参见文章指数函数的特征描述（英语：Characterizations of the exponential function）。

性质

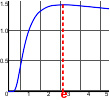
xx{\displaystyle {\sqrt[{x}]{x}}} 的极大值在x=e.

很多增长或衰减过程都可以用指数函数模拟。指数函数ex{\displaystyle e^{x}} 的重要性，在于它是唯一的函数（零多项式函数除外）与自身导数相等（乘以常数，最一般的函数形式为 kex{\displaystyle ke^{x}} ，k 为任意常数）。即:

x为复数时依然成立，因此根据sin⁡ ⁡ -->x{\displaystyle \sin x}及cos⁡ ⁡ -->x{\displaystyle \c泰勒 x}的泰勒级数，得出在数学中一条称为欧拉公式的重要等式：

当x=π π -->{\displaystyle x=\pi }的欧拉恒等式恒等式：

此式被理查德·费曼称为“欧拉的宝石”。

(cos⁡ ⁡ -->x+isin⁡ ⁡ -->x)n=(eix)n=einx=cos⁡ ⁡ -->(nx)+isin⁡ ⁡ -->(nx){\displaystyle (\cos x+i\sin x)^{n}=\left(e^{ix}\right)^{n}=e^{inx}=\cos(nx)+i\sin(nx)}

即棣莫弗公式。

e 是无理数和超越数（见林德曼－魏尔斯特拉斯定理）。这是第一个获证为超越数的数，而非故意构造的（比较刘维尔数）；由夏尔·埃尔米特（Charles Hermite）于1873年证明。有猜想它为正规数。

当x=e{\displaystyle x=e}时函数f(x)=xx{\displaystyle f(x)={\sqrt[{x}]{x}}}有最大值。

e 的无穷连分数展开式有个有趣的模式，可以表示如下（A003417）：

就像以下的展开式：

无理数证明

反证法

证明 e 是无理数可以用反证法。假设 e 是有理数，则可以表示成ab{\displaystyle {\tfrac {a}{b}}} ，其中 a,b 为正整数。以 e 的无穷级数展开式可以得出矛盾。

考虑数字

以下将推导出x{\displaystyle x}是小于1的正整数；由于不存在这样的正整数，得出矛盾，所以得证e{\displaystyle e}是无理数。

x{\displaystyle x}是整数，因为

x{\displaystyle x}是小于1的正数，因为

但是0与1之间（不含0与1）不存在有整数，故原先假设矛盾，得出e{\displaystyle e}为无理数。

二项式定理

视n{\displaystyle n}为存在的数值，所以用二项式定理可证出：

已知位数

高精度计算e程序(C++)

#includeusingnamespacestd;intmain(void){longN,a,b,i,j=0,k=0;cout<>N,N+=5;long*e=newlong[N],*c=newlong[N];while(++j<N)e[j]=c[j]=0;for(*c=i=1;k<N;i++){while(!c[k])k++;for(b=0,j=k-1;++j<N;b=a%i)e[j]+=(c[j]=(a=b*10+c[j])/i);}for(;--j;e[j]%=10)e[j-1]+=e[j]/10;for(cout<<"2.";++j<N-5;)cout<<e[j];delete[]e,delete[]c;return0;}

谐取

在Google2004年的首次公开募股，集资额不是通常的整头数，而是$2,718,281,828，这当然是取最接近整数的e{\displaystyle e}十亿美元。（顺便一提，Google2005年的一次公开募股中，集资额是$14,159,265，与圆周率有关）

Google也是首先在硅谷心脏地带，接着在马萨诸塞州剑桥出现的神秘广告版的幕后黑手，它写着{first 10-digit prime found in consecutive digits of e}.com（在e的连续数字中第一个发现的十位质数.com）。解决了这问题（第一个e{\displaystyle e}中的十位质数是7427466391，出奇地到很后才出现，由第100个数字开始），进入网站后还有个更难的题目要解决，最后会到达Google的招聘页。但这个挑战已结束，上述网站都已关闭。

著名计算机科学家高德纳的软件Metafont的版本号码趋向e{\displaystyle e}（就是说版本号码是2，2.7，2.71，2.718等），与之相对的有TeX的版本号是趋向于圆周率的。

参见

无理数

超越数

欧拉数

圆周率

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。