重要的恒等式

运算法则

同底数幂相乘，底数不变，指数相加：

同底数幂相除，底数不变，指数相减：

幂的乘方，底数不变，指数相乘：

同指数幂相乘，指数不变，底数相乘：

同指数幂相除，指数不变，底数相除：

其他等式

a m n = a m n {\displaystyle a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}}

x − − --> m = 1 x m ( x ≠ ≠ --> 0 ) {\displaystyle x^{-m}={\frac {1}{x^{m}}}\qquad (x\neq 0)}

x 0 = 1 ( x ≠ ≠ --> 0 ) {\displaystyle x^{0}=1\qquad (x\neq 0)}

x 1 = x {\displaystyle x^{1}=x\,\!}

x − − --> 1 = 1 x ( x ≠ ≠ --> 0 ) {\displaystyle x^{-1}={\frac {1}{x}}\qquad (x\neq 0)}

( x m ) n = x m n {\displaystyle (x^{m})^{n}=x^{mn}}

x i = e i ln ⁡ ⁡ --> x = cos ⁡ ⁡ --> ( ln ⁡ ⁡ --> x ) + i sin ⁡ ⁡ --> ( ln ⁡ ⁡ --> x ) , i 2 = − − --> 1 {\displaystyle x^{i}=e^{i\ln x}=\cos(\ln x)+i\sin(\ln x),\quad i^{2}=-1}

运算律

加法和乘法遵守交换律，比如：2+3 = 5 = 3+2，2×3 = 6 = 3×2，但是幂的运算不遵守交换律， 2 3 = 8 {\displaystyle 2^{3}=8} ，但是 3 2 = 9 {\displaystyle 3^{2}=9} 。

同样，加法和乘法遵守结合律，比如：(2+3)+4 = 9 = 2+(3+4)，(2×3)×4 = 24 = 2×(3×4)，幂同样不遵守： ( 2 3 ) 4 = 8 4 = 4096 {\displaystyle (2^{3})^{4}=8^{4}=4096} ，但是 2 ( 3 4 ) = 2 81 = 2 , 417 , 851 , 639 , 229 , 258 , 349 , 412 , 352 {\displaystyle 2^{(3^{4})}=2^{81}=2,417,851,639,229,258,349,412,352} 。

幂的运算顺序通常由上到下：

整数指数幂

整数指数幂的运算只需要初等代数的知识。

正整数指数幂

表达式 a 2 = a ⋅ ⋅ --> a {\displaystyle a^{2}=a\cdot a} 被称作a的平方，因为边长为a的正方形面积是 a 2 {\displaystyle a^{2}} 。

表达式 a 3 = a ⋅ ⋅ --> a ⋅ ⋅ --> a {\displaystyle a^{3}=a\cdot a\cdot a} 被称作a的立方，因为边长为a的正方体体积是 a 3 {\displaystyle a^{3}} 。

所以 3 2 {\displaystyle 3^{2}} 读作3的平方， 2 3 {\displaystyle 2^{3}} 读作2的立方。

指数表示的是底数反复相乘多少次。比如 3 5 = 3 × × --> 3 × × --> 3 × × --> 3 × × --> 3 = 243 {\displaystyle 3^{5}=3\times 3\times 3\times 3\times 3=243} ，指数是5，底数是3，表示3反复相乘5次。

或者，整数指数幂可以递归地定义成：

指数是1或者0

注意 3 1 {\displaystyle 3^{1}} 表示仅仅1个3的乘积，就等于3。

注意 3 5 = 3 × × --> 3 4 {\displaystyle 3^{5}=3\times 3^{4}} ， 3 4 = 3 × × --> 3 3 {\displaystyle 3^{4}=3\times 3^{3}} ， 3 3 = 3 × × --> 3 2 {\displaystyle 3^{3}=3\times 3^{2}} ， 3 2 = 3 × × --> 3 1 {\displaystyle 3^{2}=3\times 3^{1}} ，

继续，得到 3 1 = 3 × × --> 3 0 = 3 {\displaystyle 3^{1}=3\times 3^{0}=3} ，所以 3 0 = 1 {\displaystyle 3^{0}=1}

另一个得到此结论的方法是：通过运算法则 x n x m = x n − − --> m {\displaystyle {\frac {x^{n}}{x^{m}}}=x^{n-m}}

当 m = n {\displaystyle m=n} 时， 1 = x n x n = x n − − --> n = x 0 {\displaystyle 1={\frac {x^{n}}{x^{n}}}=x^{n-n}=x^{0}}

任何数的1次方是它本身。

负数指数

我们定义任何不为0的数的-1次方等于它的倒数。

对于非零a定义 a − − --> n = 1 a n {\displaystyle a^{-n}={\frac {1}{a^{n}}}} 。因为当 a = 0 {\displaystyle a=0} 时分母是0而没有意义。

这个定义是因为 a m ⋅ ⋅ --> a n = a m + n {\displaystyle a^{m}\cdot a^{n}=a^{m+n}} ，当m=-n时

因为 a 0 {\displaystyle a^{0}} 已经定义了，所以 a − − --> n = 1 a n {\displaystyle a^{-n}={\frac {1}{a^{n}}}} 。

或者还可以像定义a的0次方一样定义：

通过运算法则 x m x n = x m − − --> n {\displaystyle {\frac {x^{m}}{x^{n}}}=x^{m-n}}

当 m = 0 {\displaystyle m=0} 时，可以约去分子得 x − − --> n = x 0 − − --> n = x 0 x n {\displaystyle x^{-n}=x^{0-n}={\frac {x^{0}}{x^{n}}}}

负数指数 a − − --> n {\displaystyle a^{-n}} 还可以表示成1连续除以n个a。比如：

特殊数的幂

10的幂

在十进制的计数系统中，10的幂写成1后面跟着很多个0。例如： 10 3 = 1000 ,   10 − − --> 3 = 0.001 {\displaystyle 10^{3}=1000,\ 10^{-3}=0.001}

因此10的幂用来表示非常大或者非常小的数字。如：299,792,458（真空中光速，单位是米每秒），可以写成 2.99792458 × × --> 10 8 {\displaystyle 2.99792458\times 10^{8}} ，近似值 2.998 × × --> 10 8 {\displaystyle 2.998\times 10^{8}} .

国际单位制词头也使用10的幂来描述特别大或者特别小的数字，比如：词头“千”就是 10 3 {\displaystyle 10^{3}} ，词头“毫”就是 10 − − --> 3 {\displaystyle 10^{-3}}

2的幂

1的幂

1的任何次幂都为1

0的幂

0的正数幂都等于0。

0的负数幂没有定义。

任何非0之数的0次方都是1；而0的0次方是悬而未决的，某些领域下常用的惯例是约定为1。 

负1的幂

-1的奇数幂等于-1

-1的偶数幂等于1

指数非常大时的幂

一个大于1的数的幂趋于无穷大，一个小于-1的数的幂趋于负无穷大

一个绝对值小于1的数的幂趋于0

1的幂永远都是1

如果数a趋于1而它的幂趋于无穷，那么极限并不一定是上面几个。一个很重要的例子是：

参见e的幂

其他指数的极限参见幂的极限

正实数的实数幂

一个正实数的实数幂可以通过两种方法实现。

有理数幂可以通过N次方根定义，任何非0实数次幂都可以这样定义

自然对数可以被用来通过指数函数定义实数幂

N次方根

  从上到下： x 1 8 ,   x 1 4 ,   x 1 2 ,   x 1 ,   x 2 ,   x 4 ,   x 8 {\displaystyle x^{\frac {1}{8}},\ x^{\frac {1}{4}},\ x^{\frac {1}{2}},\ x^{1},\ x^{2},\ x^{4},\ x^{8}}

一个数a的n次方根是x，x使 x n = a {\displaystyle x^{n}=a} 。

如果a是一个正实数，n是正整数，那么方程 x n = a {\displaystyle x^{n}=a} 只有一个正实数根。 这个根被称为a的n次方根，记作： a n {\displaystyle {\sqrt[{n}]{a}}} ，其中   {\displaystyle {\sqrt {\ }}} 叫做根号。或者，a的n次方根也可以写成 a 1 n {\displaystyle a^{\frac {1}{n}}} . 例如 4 1 2 = 2 ,   8 1 3 = 2 {\displaystyle 4^{\frac {1}{2}}=2,\ 8^{\frac {1}{3}}=2}

当指数是 1 2 {\displaystyle {\frac {1}{2}}} 时根号上的2可以省略，如： 4 = 4 2 = 2 {\displaystyle {\sqrt {4}}={\sqrt[{2}]{4}}=2}

有理数幂

有理数指数通常可以理解成

e的幂

这个重要的数学常数e，有时叫做欧拉数，近似2.718，是自然对数的底。它提供了定义非整数指数幂的一个方法。 它是从以下极限定义的：

指数函数的定义是：

可以很简单地证明e的正整数k次方 e k {\displaystyle e^{k}} 是：

实数指数幂

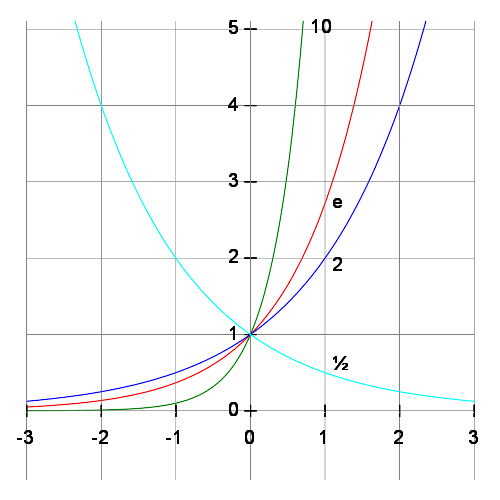
 y = b对各种底数b的图像，分别为绿色的10、红色的e、蓝色的2和青色的1/2。

因为所有实数可以近似地表示为有理数，任意实数指数x可以定义成：

例如：

于是

实数指数幂通常使用对数来定义，而不是近似有理数。

自然对数 ln ⁡ ⁡ --> x {\displaystyle \ln {x}} 是指数函数 e x {\displaystyle e^{x}} 的反函数。 它的定义是：对于任意 b > 0 {\displaystyle b>0} ，满足

根据对数和指数运算的规则：

这就是实数指数幂的定义：

实数指数幂 b x {\displaystyle b^{x}} 的这个定义和上面使用有理数指数和连续性的定义相吻合。对于复数，这种定义更加常用。

负实数的实数幂

如果a是负数且n是偶数，那么 x n = a {\displaystyle x^{n}=a} 无实数解。 如果a是负数且n是奇数，那么 x n = a {\displaystyle x^{n}=a} 有一个负数解。

使用对数和有理数指数都不能将 a k {\displaystyle a^{k}} （其中a是负实数，k实数）定义成实数。在一些特殊情况下，给出一个定义是可行的：负指数的整数指数幂是实数，有理数指数幂对于 a m n {\displaystyle a^{\frac {m}{n}}} （n是奇数）可以使用n次方根来计算，但是因为没有实数x使 x 2 = − − --> 1 {\displaystyle x^{2}=-1} ，对于 a m n {\displaystyle a^{\frac {m}{n}}} （n是偶数）时必虚数单位数单位i。

使用对数的方法不能定义a ≤ 0时的 a k {\displaystyle a^{k}} 为实数。实际上， e x {\displaystyle e^{x}} 对于任何实数x都是正的，所以 ln ⁡ ⁡ --> ( a ) {\displaystyle \ln(a)} 对于负数没有意义。

使用有理数指数幂来逼近的方法也不能用于负数a因为它依赖于连续性。函数 f ( r ) = a r {\displaystyle f(r)=a^{r}} 对于任何正的有理数a是连续的，但是对于负数a，函数f在有些有理数r上甚至不是连续的。

例如：当a = -1，它的奇数次根等于-1。所以如果n是正奇数整数， − − --> 1 m n = − − --> 1 {\displaystyle -1^{\frac {m}{n}}=-1} 当m是奇数， − − --> 1 m n = 1 {\displaystyle -1^{\frac {m}{n}}=1} 当m是偶数。虽然有理数q使 − − --> 1 q = 1 {\displaystyle -1^{q}=1} 的集合是稠密集，但是有理数q使 − − --> 1 q = − − --> 1 {\displaystyle -1^{q}=-1} 的集合也是。所以函数 − − --> 1 q {\displaystyle -1^{q}} 在有理数域不是连续的。

正实数的复数幂

e的虚数次幂

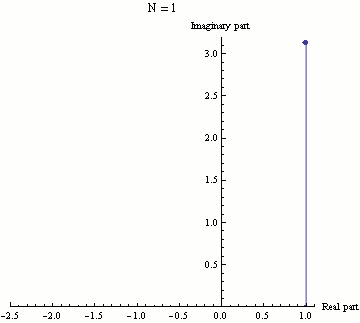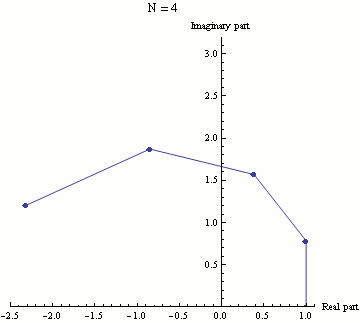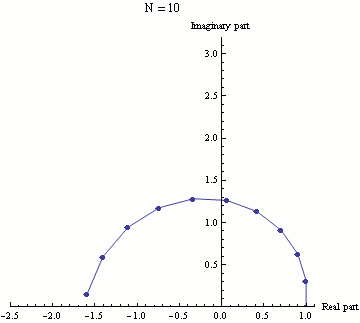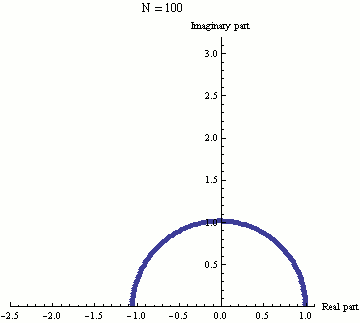
 指数函数e可以通过(1 + z/N)当N趋于无穷大时的极限来定义，那么e就是(1 + iπ/N)的极限。在这个动画中n从1取到100。(1 + iπ/N)的值通过N重复增加在复数平面上展示，最终结果就是(1 + iπ/N)的准确值。可以看出，随着N的增大，(1 + iπ/N)逐渐逼近极限-1。这就是欧拉公式。

复数运算的几何意义和e的幂可以帮助我们理解 e i x {\displaystyle e^{ix}} （x是实数）。想象一个直角三角形(0, 1, 1 + ix/n)（括号内是复数平面内三角形的三个顶点），对于足够大的n，这个三角形可以看作一个扇形，这个扇形的中心角就等于x/n弧度。对于所有k，三角形(0, (1 + ix/n), (1 + ix/n))互为相似三角形。所以当n足够大时(1 + ix/n)的极限是复数平面上的单位圆上x弧度的点。这个点的极坐标是(r, θ) = (1, x),，直角坐标是（cos x, sin x）。所以 e i x = cos ⁡ ⁡ --> x + i sin ⁡ ⁡ --> x {\displaystyle e^{ix}=\cos x+i\sin x} 。这就是欧拉公式，它通过复数的意三角学数学和三角系起来了。

等式 e z = 1 {\displaystyle e^{z}=1} 的解是一个整数乘以2iπ：

更一般地，如果 e b = a {\displaystyle e^{b}=a} ，那么 e z = a {\displaystyle e^{z}=a} 的每一个解都可以通过将2iπ的整数倍加上b得到：

这个复指数函数是一个有周期2iπ的周期函数。

更简单的： e i π π --> = − − --> 1 ;   e x + i y = e x ( cos ⁡ ⁡ --> y + i sin ⁡ ⁡ --> y ) {\displaystyle e^{i\pi }=-1;\ e^{x+iy}=e^{x}(\cos y+i\sin y)} 。

三角函数

根据欧拉公式，三角函数余弦和正弦是：

历史上，在复数发明之前，余弦和正弦是用几何的方法定义的。上面的公式将复杂的三角函数的求和公式转换成了简单的指数方程

使用了复数指数幂之后，很多三角学问题都能够使用代数方法解决。

e的复数指数幂

e x + i y {\displaystyle e^{x+iy}} 可以分解成 e x ⋅ ⋅ --> e i y {\displaystyle e^{x}\cdot e^{iy}} 。其中 e x {\displaystyle e^{x}} 是 e x + i y {\displaystyle e^{x+iy}} 的模， e i y {\displaystyle e^{iy}} 决定了 e x + i y {\displaystyle e^{x+iy}} 的方向

正实数的复数幂

如果a是一个正实数，z是任何复数， a z {\displaystyle a^{z}} 定义成 e z ⋅ ⋅ --> ln ⁡ ⁡ --> ( a ) {\displaystyle e^{z\cdot \ln(a)}} ，其中x = ln(a)是方程 e x = a {\displaystyle e^{x}=a} 的唯一解。所以处理实数的方法同样可以用来处理复数。

例如：

在函数中

当函数名后有上标的数（即函数的指数），一般指要重复它的运算。例如 f 3 ( x ) {\displaystyle f^{3}(x)} 即 f ( f ( f ( x ) ) ) {\displaystyle f(f(f(x)))} 。特别地， f − − --> 1 ( x ) {\displaystyle f^{-1}(x)} 指 f ( x ) {\displaystyle f(x)} 的反函数。

但三角函数的情况有所不同，一个正指数应用于函数的名字时，指答案要进行乘方运算，而指数为-1时则表示其反函数。例如： ( sin ⁡ ⁡ --> x ) − − --> 1 {\displaystyle (\sin x)^{-1}} 表示 csc ⁡ ⁡ --> x {\displaystyle \csc x} 。因此在三角函数时，使用 sin − − --> 1 ⁡ ⁡ --> x {\displaystyle \sin ^{-1}x} 来表示 sin ⁡ ⁡ --> x {\displaystyle \sin x} 的反函数 arcsin ⁡ ⁡ --> x {\displaystyle \arcsin x} 。

在抽象代数中

计算自然数（正整数）n的a的算法

最快的方式计算 a n {\displaystyle a^{n}} ，当n是正整数的时候。它利用了测试一个数是奇数在计算机上是非常容易的，和通过简单的移所有位向右来除以2的事实。

伪代码：

1. 1 → y, n → k, a → f 2.若k不為0,執行3至6 3.若k為奇數, y * f → y 4. k [[位操作#移位|右移]]1位（即k / 2 → k ,小數點無條件捨去） 5. f * f → f 6.回到2 7.傳回y

在C/C++语言中，你可以写如下算法：

doublepower(doublea,unsignedintn){doubley=1;doublef=a;unsignedintk=n;while(k!=0){if(k%2==1)y*=f;k>>=1;f*=f;}returny;}

此算法的时间复杂度为 O ( log ⁡ ⁡ --> n ) {\displaystyle \mathrm {O} (\log n)\!} ，比普通算法快（a自乘100次，时间复杂度为 O ( n ) {\displaystyle \mathrm {O} (n)\!} ），在n较大的时候更为显著。

例如计算 a 100 {\displaystyle a^{100}} ，普通算法需要算100次，上述算法则只需要算7次。若要计算 a n ( n < 0 ) {\displaystyle a^{n}(n<0)} 可先以上述算法计算 a | n | {\displaystyle a^{|n|}} ，再作倒数。

另见

迭代幂次

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。