函数图形
样例单变量函数一次函数三个线性函数的图形都是直线。红色与蓝色直线的斜率相同。红色与绿色直线的y-截距相同。形如的图像为:在平面直角坐标系中,该图像为一条直线。这是因为,该函数的导数为常数k{displaystylek}。非线性函数函数f(x)=x3−−-->9x{displaystylef(x)
样例
单变量函数
一次函数
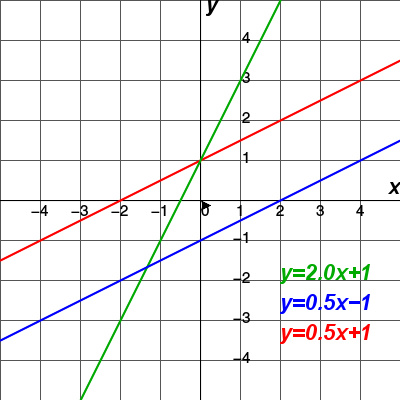
三个线性函数的图形都是直线。红色与蓝色直线的斜率相同。 红色与绿色直线的 y-截距相同。
形如
的图像为:
在平面直角坐标系中,该图像为一条直线。这是因为,该函数的导数为常数k{\displaystyle k}。
非线性函数
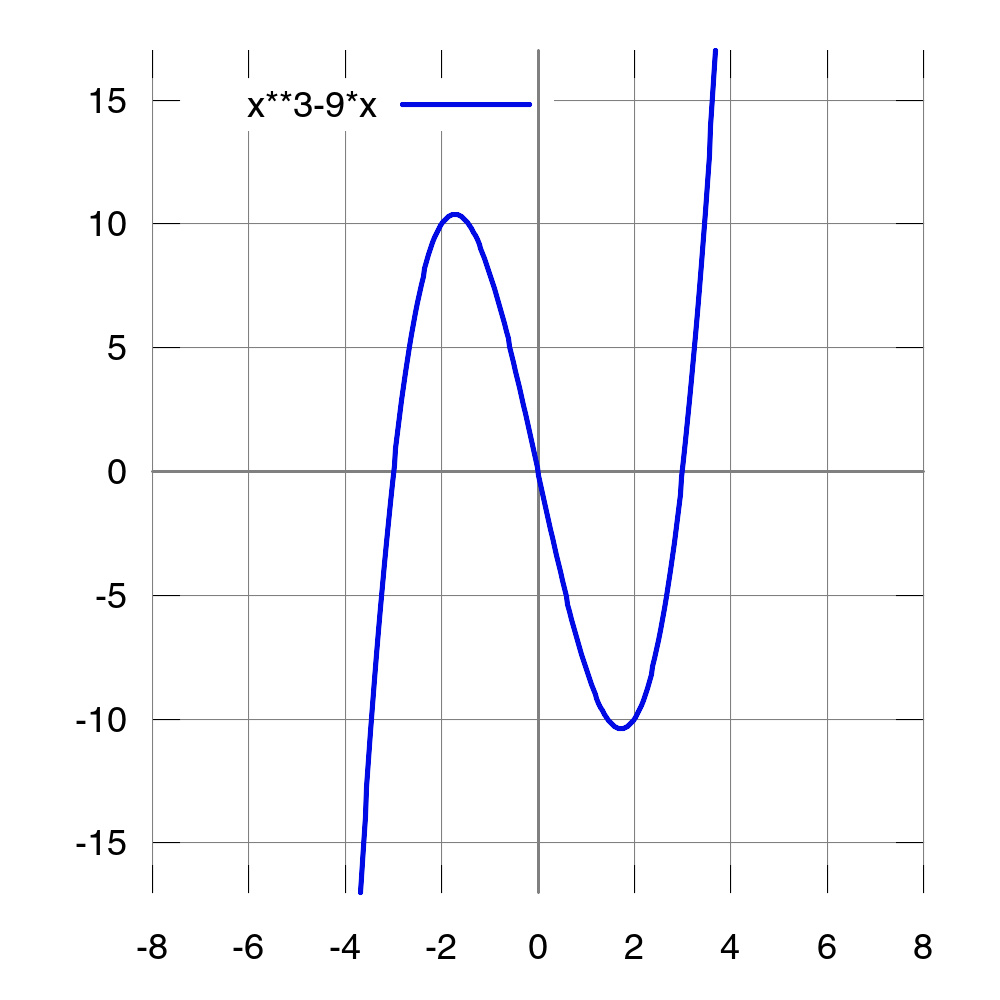
函数 f(x)=x3− − -->9x{\displaystyle f(x)=x^{3}-9x} 的图像。
对于二次或更高次的多项式函数,或者其他的非线性函数,其图像则会呈现为一条曲线。这是因为其导函数不是常数函数。
例如,三次函数
的图像为
如果将这个图像绘制在平面直角坐标系中,则会得到一条三次曲线(见右图)。
双变量函数
函数f(x,y)=sin -->(x2)× × -->cos -->(y2){\displaystyle {\begin{smallmatrix}f(x,y)=\sin(x^{2})\times \cos(y^{2})\end{smallmatrix}}} 的图像。
三角学中的函数
的图像为
如果这个图像绘制在了三维坐标系中,则会得到一个曲面(见图)。
函数图像绘制工具
硬件

TI-83绘图计算器。
图形计算器
示波器
软件
更多资料:动态几何软件
参考文献
Weisstein, Eric W. "Function Graph - MathWorld."
相关条目
函数
导数
驻点
斜率
截距
方程
坐标系
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
文章来源:内容词条
——— 没有了 ———
编辑:阿族小谱

相关资料
展开
文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~



打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 正图形
分类和描述正图形最基础的分类是按其维度。它们能够按照对称性进一步分类。例如,正方体和正八面体有着相同的对称性,同样,正十二面体和正二十面体也是。事实上,对称群大多依照正图形命名,例如正四面体对称群和正二十面体对称群。3种特殊类型的正图形存在于所有维度:单纯形(正单形)超方形(正测形)正轴形(交叉形)在二维,这里有无穷多个正多边形。在三维和四维这里有许多上述三种之外的正多面体和正多胞体。在五维及以上维,只存在这三种类型的正图形。另见正图形列表。正图形的概念有时被扩展,使其包括了另外一些相关的几何对象。其中一些有正的例子,下面“历史发现”一章将会详细说明。施莱夫利符号施莱夫利符号是一个简洁有力的多面体表示法,是19世纪由路德维希·施莱夫利所发明的,一个改进了的版本随后成为了标准。这种记号可通过维度依次增加一获得最好的解释。一个有n条边的凸正多边形可以标记为{n}。所以一个等边三角形是{3},一
· 硅谷图形公司

SGI产品线当前的SGI产品MIPS-basedsystemsFuelentry-levelworkstationTezrohigh-endworkstationOrigin350mid-rangeserverOrigin3000high-endserverIntelXeon-basedsystemsAltixXE-seriesserversItanium-basedsystemsPrismhigh-endworkstationAltix330mid-rangeserverAltix350mid-rangeserverAltix3000high-endserverAltix4000high-endserver过去的SGI产品Motorola68k-basedsystemsSGIIRIS1000系列SGIIRIS2000系列SGIIRIS3000系列MIPS-basedsystemsSGII...
· Γ函数

定义ΓΓ-->{\displaystyle\Gamma\,}函数可欧拉过欧拉(Euler)第二类积分定义:对复数z{\displaystylez\,},我们要求Re(z)>0{\displaystyle\mathrm{Re}(z)>0}。ΓΓ-->{\displaystyle\Gamma}函数还可以通过对e−−-->t{\displaystyle\mathrm{e}^{-泰勒\,}做泰勒展开,解析延拓到整个复平面:ΓΓ-->(z)=∫∫-->1∞∞-->tz−−-->1etdt+∑∑-->n=0∞∞-->(−−-->1)nn!1n+z{\displaystyle\Gamma(z)=\int_{1}^{\infty}{\frac{t^{z-1}}{\mathrm{e}^{t}}}{\rm{d}}t+\sum_{n=0}^...
· 函数

定义函数f的部分图像。每个实数的x都与f(x)=x−9x相联系。从输入值集合X{\displaystyleX}到可能的输出值集合Y{\displaystyleY}的函数f{\displaystylef}(记作f:X→→-->Y{\displaystylef:X\toY})是X{\displaystyleX}与Y{\displaystyleY关系的关系,满足如下条件:f{\displaystylef}是完全的:对集合X{\displaystyleX}中任一元素x{\displaystylex}都有集合Y{\displaystyleY}中的元素y{\displaystyley}满足xfy{\displaystylexfy}(x{\displaystylex}与y{\displaystyley}是f{\displaystylef}相关的)。即,对每一个输入值,y{\displaystyle...
· 计算机图形

概况计算机图形在学术中的广义被用来描述为“在计算机里除了文字与声音以外的一切”。通常,计算机图形在学术上指以下事情:用计算机表现或处理图像数据用于创建或处理图像的各种技术经过制作的图像计算机科学分领域的数字合成和处理视觉内容的研究,参见计算机图形学现在,计算机和计算机生成图像接触到日常生活的多个层面。计算机图像出现在电视、报纸等地方,同时在天气预报、医疗调查和手术操作等产生作用。一个精心构筑的图表可以将复杂的统计以更容易理解和解释的方式呈现。在媒体中,“这样的图表可以被用于说明文件、报告、论文”,和用于其它演示材料。已经开发出许多功能强大的工具将数据可视化。计算机生成图像可以被分成几种类型:二维、三维和动画。随着技术的改进,三维计算机图形变得越来越常见,但二维计算机图形仍然被广泛使用。在过去的十年中,发展出在其它专门领域的应用,如:信息可视化和科学可视化,其中更多涉及到“三维现象的可视化(...
知识互答
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}