历史

  路易·德布罗意

  埃尔温·薛定谔

在1920年代与1930年代，理论量子物理学者大致分为两个阵营。第一个阵营的成员主要为路易·德布罗意和埃尔温·薛定谔等等，他们使用的数学工具是微积分，他们共同创建了波动力学。第二个阵营的成员主要为维尔纳·海森堡和马克斯·玻恩等等，使用线性代数，他们建立了矩阵力学。后来，薛定谔证明这两种方法完全等价。

德布罗意于1924年提出的德布罗意假说表明，每一种微观粒子都具有波粒二象性。电子也不例外，具有这种性质。电子是一种波动，是电子波。电子的能量与动量分别决定了它的物质波频率与波数。既然粒子具有波粒二象性，应该会有一种能够正确描述这种量子特性的波动方程，这点子给予埃尔温·薛定谔极大的启示，他因此开始寻找这波动方程。薛定谔参考威廉·哈密顿先前关于牛顿力学与光学之间的类比这方面的研究，在其中隐藏了一个奥妙的发现，即在零波长极限，物理光学趋向于几何光学；也就是说，光波的轨道趋向于明确的路径，而这路径遵守最小作用量原理。哈密顿认为，在零波长极限，波传播趋向于明确的运动，但他并没有给出一个具体方程来描述这波动行为，而薛定谔给出了这方程。他从哈密顿-雅可比方程成功地推导出薛定谔方程。 他又用自己设计的方程来计算氢原子的谱线，得到的答案与用玻尔模型计算出的答案相同。他将这波动方程与氢原子光谱分析结果，写为一篇论文，1926年，正式发表于物理学界 。从此，量子力学有了一个崭新的理论平台。

薛定谔给出的薛定谔方程能够正确地描述波函数的量子行为。那时，物理学者尚未能解释波函数的涵义，薛定谔尝试用波函数来代表电荷的密度，但遭到失败。1926年，玻恩提出概率幅的概念，成功地解释了波函数的物理意义 。可是，薛定谔本人不赞同这种统计或概率方法，和它所伴随的非连续性波函数坍缩，如同爱因斯坦认为量子力学只是个决定性理论的统计近似，薛定谔永远无法接受哥本哈根诠释。在他有生最后一年，他写给玻恩的一封信内，薛定谔清楚地表明了这意见。

1927年，道格拉斯·哈特里（Douglas Hartree）与弗拉基米尔·福克（Vladimir Fock）在对于多体波函数的研究踏出了第一步，他们发展出哈特里－福克方程来近似方程的解。这计算方法最先由哈特里提出，后来福克将之加以改善，能够符合泡利不相容原理的要求。

薛定谔方程不具有洛伦兹不变性，无法准确给出符合相对论的结果。薛定谔试着用相对论的能量动量关系式，来寻找一个相对论性方程，并且描述电子的相对论性量子行为。但是这方程给出的精细结构不符合阿诺·索末菲的结果，又会给出违背量子力学的负概率和怪异的负能量现象，他只好将这相对论性部分暂时搁置一旁，先行发表前面提到的非相对论性部分。

1926年，奥斯卡·克莱因（Oskar Klein）和沃尔特·戈尔登（Walter Gordon）将电磁相对作用纳入考量，独立地给出薛定谔先前推导出的相对论性部分，并且证明其具有洛伦兹不变性。这方程后来称为克莱因-戈尔登方程。

1928年，保罗·狄拉克最先成功地统一了狭义相对论与量子力学，他推导出狄拉克方程，适用于电子等等自旋为1/2的粒子。这方程的波函数是一个旋量，拥有自旋性质。

概述

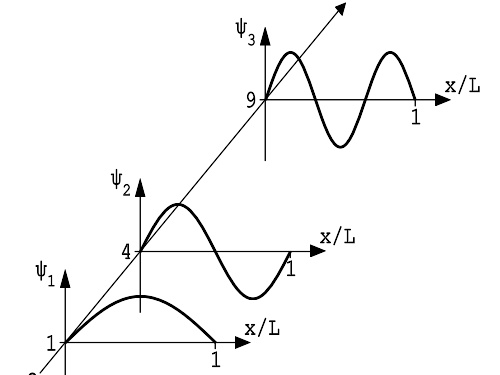
  在一维无限深方形阱内，粒子的能级与对应的波函数。

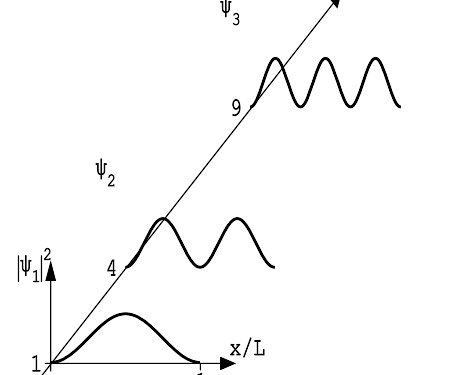
  在一维无限深方形阱内，找到能级为 n {\displaystyle n} 的粒子的概率。

位置空间波函数

假设一个自旋为零的粒子移动于一维空间。这粒子的量子态以波函数表示为 Ψ Ψ --> ( x , t ) {\displaystyle \Psi (x,t)} ；其中， x {\displaystyle x} 是位置， t {\displaystyle t} 是时间。波函数是复值函数。测量粒子位置所得到的结果不是决定性的，而是概率性的。粒子的位置 x {\displaystyle x} 在区间 [ a , b ] {\displaystyle [a,b]} （即 a ≤ ≤ --> x ≤ ≤ --> b {\displaystyle a\leq x\leq b} ）的概率 P a ≤ ≤ --> x ≤ ≤ --> b {\displaystyle P_{a\leq x\leq b}} 为

其中， t {\displaystyle t} 是对于粒子位置做测量的时间。

换句话说， | Ψ Ψ --> ( x , t ) | 2 {\displaystyle |\Psi (x,t)|^{2}} 是粒子在位置 x {\displaystyle x} 、时间 t {\displaystyle t} 的概率密度。

这导致归一化条件：在位置空间的任意位置找到粒子的概率为100%：

动量空间波函数

在动量空间，粒子的波函数表示为 Φ Φ --> ( p , t ) {\displaystyle \Phi (p,t)} ；其中， p {\displaystyle p} 是一维动量，值域从 − − --> ∞ ∞ --> {\displaystyle -\infty } 至 + ∞ ∞ --> {\displaystyle +\infty } 。测量粒子动量所得到的结果不是决定性的，而是概率性的。粒子的动量 p {\displaystyle p} 在区间 [ a , b ] {\displaystyle [a,b]} （即 a ≤ ≤ --> p ≤ ≤ --> b {\displaystyle a\leq p\leq b} ）的概率为

动量空间波函数的归一化条件也类似：

两种波函数之间的关系

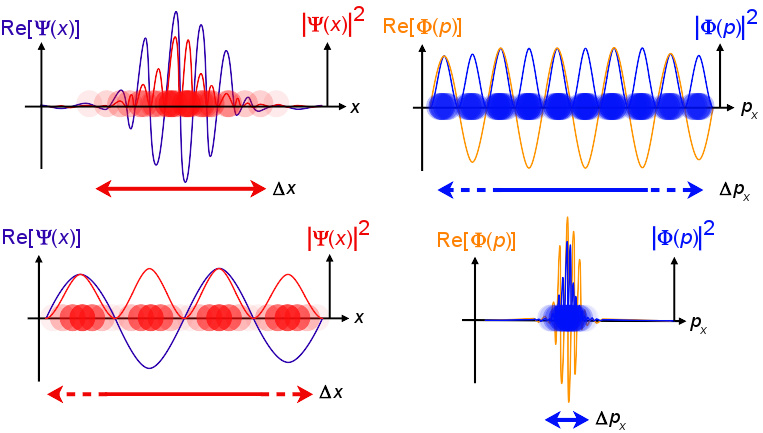
  本图展示一维零自旋自由粒子的波函数范例，左边是位置空间波函数 Ψ Ψ --> ( x ) {\displaystyle \Psi (x)} 的实部（紫色）和概率密度 | Ψ Ψ --> ( x ) | 2 {\displaystyle |\Psi (x)|^{2}} （红色），右边是动量空间波函数 Φ Φ --> ( p ) {\displaystyle \Phi (p)} 的实部（金色）和概率密度 | Φ Φ --> ( p ) | 2 {\displaystyle |\Phi (p)|^{2}} （蓝色）。在x-轴的某位置 x {\displaystyle x} 或p x -轴的某动量 p {\displaystyle p} 显示出的粒子颜色的不透明度，分别表示在那位置 x {\displaystyle x} 或动量 p {\displaystyle p} 找到粒子的概率密度（不是波函数的概率幅）。

位置空间波函数与动量空间波函数彼此是对方的傅里叶变换。他们各自拥有的信息相同，任何一种波函数都可以用来计算粒子的相关性质。两种波函数之间的关系为

薛定谔方程

在一维空间里，运动于位势 V ( x ) {\displaystyle V(x)} 的单独粒子，其波函数满足含时薛定谔方程

其中， m {\displaystyle m} 是质量， ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数。

不含时薛定谔方程与时间无关，可以用来计算粒子的本征能量与其它相关的量子性质。应用分离变数法，猜想 Ψ Ψ --> ( x , t ) {\displaystyle \Psi (x,\,t)} 的函数形式为

其中， E {\displaystyle E} 是分离常数，稍加推导可以论定 E {\displaystyle E} 就是能量， ψ ψ --> E ( x ) {\displaystyle \psi _{E}(x)} 是对应于 E {\displaystyle E} 的本征函数。

代入这猜想解，经过一番运算，可以推导出一维不含时薛定谔方程：

波函数的概率诠释

波函数 Ψ Ψ --> ( r , t ) {\displaystyle \Psi (\mathbf {r} ,t)} 是概率波。其模的平方 | Ψ Ψ --> ( r , t ) | 2 {\displaystyle \vert \Psi (\mathbf {r} ,t)\vert ^{2}\,} 代表粒子在该处出现的概率密度，并且具有归一性，全空间的积分

波函数的另一个重要特性是相干性。两个波函数叠加，概率的大小取决于两个波函数的相位差，类似光学中的杨氏双缝实验。

波函数的本征值和本征态

在量子力学中，可观察量 A {\displaystyle A} 以算符 A ^ ^ --> {\displaystyle {\hat {A}}} 的形式出现。 A ^ ^ --> {\displaystyle {\hat {A}}} 代表对于波函数的一种运算。例如，在位置空间里，动量算符 p ^ ^ --> {\displaystyle {\hat {\mathbf {p} }}} 的形式为

可观察量 A {\displaystyle A} 的本征方程为

对应的 a {\displaystyle a} 称为算符 A ^ ^ --> {\displaystyle {\hat {A}}} 的本征值， ψ ψ --> {\displaystyle \psi } 称为算符 A ^ ^ --> {\displaystyle {\hat {A}}} 的本征态。假设对于 A ^ ^ --> {\displaystyle {\hat {A}}} 的本征态 ψ ψ --> {\displaystyle \psi } 再测量可观察量 A {\displaystyle A} ，则得到的结果是本征值 a {\displaystyle a} 。

态叠加原理

假设对于某量子系统测量可观察量 A {\displaystyle A} ，而可观察量 A {\displaystyle A} 的本征态 | a 1 〉 〉 --> {\displaystyle |a_{1}\rangle } 、 | a 2 〉 〉 --> {\displaystyle |a_{2}\rangle } 分别拥有本征值 a 1 {\displaystyle a_{1}} 、 a 2 {\displaystyle a_{2}} ，则根据薛定谔方程的线性关系，叠加态 | ψ ψ --> 〉 〉 --> {\displaystyle |\psi \rangle } 也可以是这量子系统的量子态：

其中， c 1 {\displaystyle c_{1}} 、 c 2 {\displaystyle c_{2}} 分别为叠加态处于本征态 | a 1 〉 〉 --> {\displaystyle |a_{1}\rangle } 、 | a 2 〉 〉 --> {\displaystyle |a_{2}\rangle } 的概率幅。

假设对这叠加态系统测量可观察量 A {\displaystyle A} ，则测量获得数值是 a 1 {\displaystyle a_{1}} 或 a 2 {\displaystyle a_{2}} 的概率分别为 | c 1 | 2 {\displaystyle |c_{1}|^{2}} 、 | c 2 | 2 {\displaystyle |c_{2}|^{2}} ，期望值为

定态

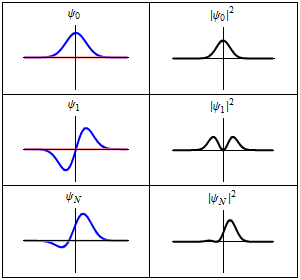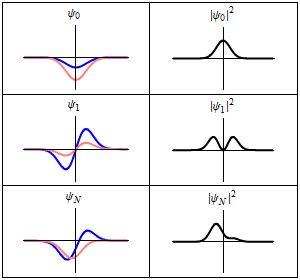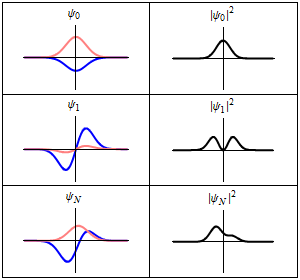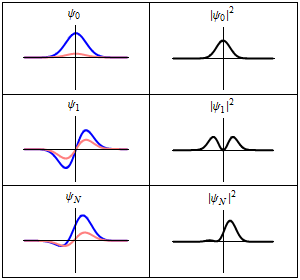
  描述谐振子的含时薛定谔方程的三个波函数解。左边：波函数概率幅的实部（蓝色）或虚部（红色）。右边：找到粒子在某位置的概率，这说明了为什么概率与时间无关的量子态被称为“定态”。上面两个横排是定态，最下面横排是叠加态 ψ ψ --> N = ( ψ ψ --> 0 + ψ ψ --> 1 ) / 2 {\displaystyle \psi _{N}=(\psi _{0}+\psi _{1})/{\sqrt {2}}}

。

在量子力学中，一类基本的问题是哈密顿算符 H ^ ^ --> {\displaystyle {\hat {H}}} 不含时间的情况。对于这问题，应用分离变数法，可以将波函数 Ψ Ψ --> ( r , t ) {\displaystyle \Psi (\mathbf {r} ,t)} 分离成一个只与位置有关的函数 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 和一个只与时间有关的函数 f ( t ) {\displaystyle f(t)} ：

将这公式代入薛定谔方程，就会得到

而 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 则满足本征能量薛定谔方程：

例子

自由粒子

3D空间中的自由粒子，其波矢为 k ，角频率为 ω ，其波函数为：

无限深方形阱

粒子被限制在 x = 0 和 x = L 之间的1D空间中，其波函数为:

其中， ℏ ℏ --> ω ω --> n = n 2 h 2 8 m L 2 {\displaystyle \hbar \omega _{n}={\frac {n^{2}h^{2}}{8mL^{2}}}} 是能量本征值， n {\displaystyle n} 是正整数， m {\displaystyle m} 是质量。

有限位势垒

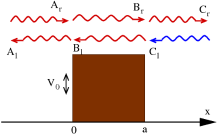
  对于一个垒高为 V_0\,\! 的位势垒的散射。往左与往右的量子波的波幅与方向都分别表示于图内。用来计算透射系数与反射系数的量子波都以红色表示

在1D情况下，粒子处于如下势垒中：

其波函数的定态解为( k , κ κ --> {\displaystyle k,\kappa } 为常数)

量子点

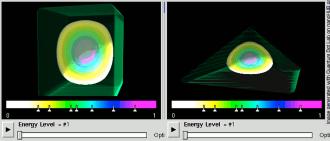
  量子点中3D受束缚的电子波函数。如图所示为方形和三角形量子点。方形量子点中的电子态更像s轨道和p轨道。然而，由于不同的几何形态导致不同的束缚，三角形量子点中的波函数则是多种轨道混合的结果。

量子点 是在把激子在三个空间方向上束缚住的半导体纳米结构。粒子在三个方向上都处在势阱中。势阱可以由于静电势（由外部的电极，掺杂，应变，杂质产生），两种不同半导体材料的界面（例如：在自组量子点中），半导体的表面（例如：半导体纳米晶体），或者以上三者的结合。量子点具有分离的量子化的能谱。所对应的波函数在空间上位于量子点中，但延伸于数个晶格周期中。其中的能级可以用类似无限深方形阱的模型来描述，能级位置取决于势阱宽度。

参阅

波包

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。