衍射与干涉的关系

美国物理学家、诺贝尔物理学奖得主理查德·费曼指出：

他还提到，如果只有少数的波源（例如两个的时候），我们称这现象为“干涉”，例如我们称杨氏双缝实验实验中双缝所产生的两束光源产生了干涉现象。而当大量波源存在时，对应的过程被称作是“衍射”。在实际情况中，衍射和干涉往往是同时出现的。有文献这样总结：干涉是有限多个波束“相加”的结果，而衍射则是无限多个波束“积分”的结果。

研究历史

 意大利物理学者弗朗西斯科·格里马第（1618-1663）。

光的衍射效应最早是由弗朗西斯科·格里马第（ Francesco Grimaldi ）于1665年发现并加以描述，他也是“衍射”一词的创始人。 这个词源于拉丁语词汇 diffringere ，意为“成为碎片”，即波原来的传播方向被“打碎”、弯散至不同的方向。格里马第观察到的现象直到1665年才被发表，这时他已经去世。他提出

英国科学家艾萨克·牛顿对这些现象进行了研究，他认为光线发生了弯曲，并认为光是由粒子构成。在19世纪以前，由于牛顿在学界的权威，光微粒说在很长一段时间占有主流位置。这样的情况直到19世纪几项理论和实验结果的发表，才得以改变。1803年，托马斯·杨进行了一项非常著名的实验，这项实验展示了两条紧密相邻的狭缝造成的干涉现象，后人称之为“双缝实验”。 在这个实验中，一束光照射到具有紧挨的两条狭缝的遮光挡板上，当光穿过狭缝并照射到挡板后面的观察屏上，可以产生明暗相间的条纹。他把这归因于光束通过两条狭缝后衍射产生的干涉现象，并进一步推测光一定具有波动的性质。奥古斯丁·菲涅耳则对衍射做了更多权威的计算研究，他的结果分别于1815年 和1818年 被发表，他提到

法国科学院曾经举办了一个关于衍射问题的有奖辩论会，菲涅耳赢得了这次辩论。作为反对光波动说的其中一位，西莫恩·德尼·泊松提出，如果菲涅耳声称的结论是正确的，那么当光射向一个球的时候，将会在球后面阴影区域的中心找到亮斑。结果，评审委员会安排了上述实验，并发现了位于阴影区域中心的亮斑（它后来被称作泊松光斑）。这个发现极大地支持了菲涅耳的理论。 他的研究为克里斯蒂安·惠更斯发展的光的波动理论提供了很大的支持。他与杨的理论共同反驳了牛顿关于光是粒子的理论。

在对衍射现象的探索过程中，人们也不断积累了对于衍射光栅的认识。17世纪，苏格兰数学家、天文学家詹姆斯·格雷戈里（ James Gregory ）在鸟的羽毛缝间观察到了阳光的衍射现象。他是第一个发衍射光栅原理的科学家。在1673年5月13日他写给约翰·科林斯（ John Colins ）的一封信中提到了此发现。 ；1786年，美国天文学家戴维·里滕豪斯用螺丝和细线第一次人工制成了衍射光栅，细线的密度达到每英寸100线，他用这个装置成功地看到了阳光的衍射。1821年，约瑟夫·夫琅禾费利用相似的装置（每厘米127线）证明了托马斯·杨关于衍射的公式（参见段落下方），并对衍射进行了许多重要研究。1867年，刘易斯·卢瑟福（ Lewis Morris Rutherfurd ）采用水轮机作为动力进行刻线、制作光栅。后来的亨利·奥古斯塔斯·罗兰改良了光栅的刻划技术，并在1882年发明了在凹形球面镜上进行刻划的凹面光栅。其后的罗伯特·伍德（ Robert William Wood ）改进了光栅的刻划形状，从而提高了光栅的衍射效率。近代的阿尔伯特·迈克耳孙提出利用干涉伺服系统控制光栅的刻划过程，于1948年实现了这一想法。20世纪下半叶，由于激光、光刻胶等新技术的出现，光栅制造技术取得很大的进步，制造成本显著降低，制造周期也得以缩短。

日常生活中的实例

  图示为温泉上方水蒸气中的光环现象。光环是一种光波被水气或尺寸不均匀的小水滴反向散射到其波源的光学现象，整个过程包含了衍射、反射和折射。

衍射效应在日常生活中并不罕见。许多有关光的衍射实例都可以用肉眼观察到。例如，在CD或DVD光盘的表面，均匀地紧密排列着一系列的光轨，这些光轨相当于衍射光栅的作用。 如果以一定的角度观察它们，会看到光在盘面表现出类似彩虹的彩色图样。将上述现象的基本原理加以利用，很多产生有意思衍射图样的衍射光栅，都可以被制备出来。衍射也是信用卡等所采用的全息摄影的技术基础之一。 地球的大气层是由微小粒子组成的，因此它也能够使空间光源（例如太阳或者月亮）的光在大气层发生衍射，从而形成光环。此外，当激光照射到粗糙的光学界面上时，也能够发生衍射现象，产生散斑。 上述所有例子都是光具有波动性的结果。

衍射是一切波的固有属性。即使是宏观的海浪，在防波堤或其他障碍物附近也能够发生衍射。此外，声波在障碍物边缘发生衍射，也是人站在障碍物（例如墙壁、树木）后面仍然能够听到声音的原因之一。 不过，衍射也为照相机、望远镜和显微镜等光学仪器的的分辨率设定了一定的限制。

物理机制

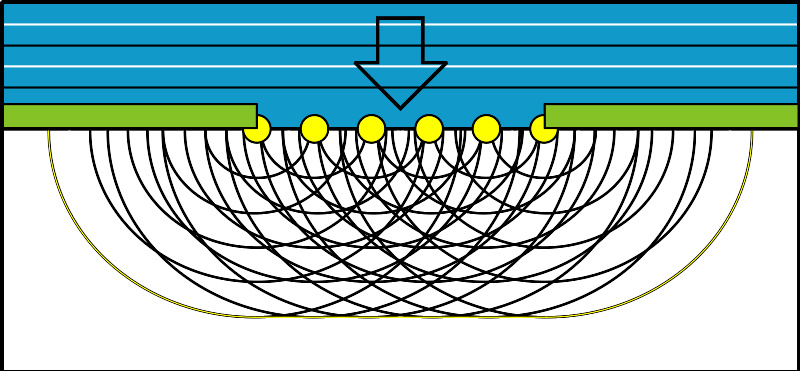
  惠更斯原理的示意图：可以看出，狭缝处诸点光源作为次生光波的光源向各个方向发出光波。

光波（或其他波）传播的路径不同，可能造成衍射现象的发生。可以用惠更斯－菲涅耳原理和波的叠加原理对现象进行描述。这个理论认为，可以把波前的每一点考虑为次波（球面波）的点波源，这些次波就是后续时刻的波面。这个原理最早由惠更斯于17世纪提出，不过他并未虑及波的时空周期性（他认为光是一种非周期性的、无规则的脉冲）。fact|1818年左右，菲涅耳在巴黎科学院关于解释衍射现象的有奖竞赛中，吸收了惠更斯“次波”的思想，并加入了他对于干涉现象的理解，使上述理论得以发展和完善。后人将这个理论称为“惠更斯－菲涅耳原理”。根据这一理论，任意后续位置的波位移等于这些次波求和。求和并非简单的代数和，而必须虑及这些波各自的相对相位以及振幅。因此，它们叠加之后的振幅范围介于0（相互完全抵消）和所有次波振幅的代数总和之间。我们可以通过光学实验，观察到光波的衍射图样。光的衍射图样通常具有一系列明暗条纹（分别对应光波振幅的最大值和最小值）。

人们为了分析波的衍射现象，构造了许多数学模型，其中包括从波动方程推导出的菲涅耳－基尔霍夫衍射公式、夫琅禾费衍射模型以及菲涅耳衍射模型。 设 a {\displaystyle a} 为圆孔半径或狭缝宽度， λ λ --> {\displaystyle \lambda } 为入射波的波长， L {\displaystyle L} 为观察屏距离圆孔、狭缝等衍射物体的距离，如果它们满足

我们就称其为菲涅耳衍射，它是衍射的近场近似；

如果它们满足

我们就称其为夫琅禾费衍射，它是衍射的远场近似。

大多数情况，获得衍射方程的严格解析解较为困难， 可以通过有限元分析和边界元分析方法来求得数值解。实际的衍射过程通常很复杂，不过，如果能够将实际情况简化到二维平面上，则对于衍射的数学描述将变得相对简单。例如，水波就可以近似地看做是分布在二维平面上的机械波。而对于光波，如果它遇到的衍射物体在某一个方向的尺度远大于光的波长，从而造成这个方向的衍射现象不显著，那么，在分析计算时可以将其忽略，这样做并不会严重影响分析结果。例如，狭缝问题就可以简化到二维的情况，这是因为其沿着缝隙方向的长度和入射光波长相差甚远，因此我们只需考虑它宽度和厚度这两个方向。然而，当我们考虑入射光穿过圆孔时，则必须完整地考虑其三维方向光的传播细节。

光的衍射

单缝衍射

  在实验中，常常利用图中的xy-可调式单缝仪来研究单缝衍射。通过四个旋钮，可以方便地对狭缝的宽度和形状进行微调，从而研究不同情况衍射的特点。

  图的右半部分为观察屏水平方向上的辐照度分布，辐照度曲线在 θ θ --> {\displaystyle \theta } -轴的第一个零点 θ θ --> m i n , 1 {\displaystyle \theta _{min,1}} 被称为“第一极小值”；图的左半部分为单缝衍射的示意图，狭缝处诸点光源发出的光波以角度 θ θ --> {\displaystyle \theta } 传播到达第一极小值。这里，我们认为这些光束与狭缝垂直平分线的夹角均为 θ θ --> {\displaystyle \theta } ，是基于 L {\displaystyle L} 远大于 d {\displaystyle d} 的前提。

假设有一个不透明挡板，用小刀在上面刻一条狭长、笔直、透光的缝，然后在挡板的后面放置一个观察屏。照射单色平行光（ collimated light ）在这个挡板上。按照几何光学，观察屏上只会有一条与狭缝轮廓相同的亮条纹。然而，精细的观察可以发现在这条亮条纹的两侧，对称地分布着一些亮条纹。发生这样现象是因为光在狭缝处发生了衍射。

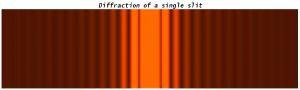
  单缝衍射强度分布图

假设狭缝宽度大于光波的波长，那么当这束光穿过狭缝后，会向挡板后的区域传播，并在那里发生干涉现象。实际上，狭缝的缝宽之间均匀分布着大量点光源，衍射图样是这些点光源的共同作用结果。为了简化对于该过程的分析，限定入射光具有单一的波长、都是单色光（频率相同），并且在波源位置具有相同的初始相位。在狭缝后面的区域中任意位置的光是上述所有点光源的“次光波”在那位置的叠加结果。 因为次光波从狭缝的每个点光源到给定点所经过的路径不同，所以它们的光程不同，因此它们在给定点的相位将会不同。对于缝间任意两个点光源，假若分别来自它们的次光波在观察屏给定点的相对相位为 2 π π --> {\displaystyle 2\pi } ，则这两个次光波会干涉相长；假若相对相位为 π π --> {\displaystyle \pi } ，则这两个次光波会干涉相消。 从这概念，可以找到衍射光强的极大值或极小值。在衍射图样中，它们分别表现为明暗条纹。

通过下面的推导， 可以找到衍射光波的第一个极小值在观察屏上的位置。将宽度为 d {\displaystyle d} 的狭缝均分为上下两段，每段长度分别为 d / 2 {\displaystyle d/2} 。考虑来自上段顶部的一束光与来自下段顶部（即狭缝中点）的一束光（波长为 λ λ --> {\displaystyle \lambda } ），这两个点光源的距离为狭缝长度的一半。当两束光传播到观察屏上距离中央极大值最近的位置（此处到狭缝中点连线垂直平分线平分线的夹角为 θ θ --> {\displaystyle \theta } ），两束光的光程差等于半个波长，即

时（在等式两边同时乘以2，可以得到 d sin ⁡ ⁡ --> θ θ --> = λ λ --> {\displaystyle d\,\sin \theta =\lambda } ），二者将发生干涉相消。现在考虑上段中点和下段中点发出的两束光，如果它们在相应位置的光程差也等于半个波长，则也能发生相似的干涉相消现象。注意，在上面的讨论中，我们已经假定狭缝与观察屏的间距远大于狭缝的宽度 L ≫ ≫ --> d {\displaystyle L\gg d} ，这样就可以近似认为狭缝间诸点光源以相同的角度 θ θ --> {\displaystyle \theta } 平行地传播到第一极小值位置。可以想象，狭缝其他位置任意两个点光源，只要满足 d sin ⁡ ⁡ --> θ θ --> m i n , 1 = λ λ --> {\displaystyle d\,\sin \theta _{min,1}=\lambda } ，那么都会在上述位置形成干涉相消，形成第一级暗纹。

回想先前的假设为狭缝宽度大于光波波长。注意到狭缝宽度越小，同时保持波长不变，则 sin ⁡ ⁡ --> θ θ --> m i n , 1 = λ λ --> / d {\displaystyle \sin \theta _{min,1}=\lambda /d} 越大， θ θ --> m i n , 1 {\displaystyle \theta _{min,1}} 也越大，因此观察屏展示的第一级暗纹离开中央越远，直到当狭缝宽度等于光波波长时， θ θ --> m i n , 1 = π π --> / 2 {\displaystyle \theta _{min,1}=\pi /2} ，在观察屏表面再也找不到第一级暗纹，整个观察屏都被明纹覆盖了。所以，只有当狭缝宽度大于光波波长时，才能够展示出衍射的干涉图样。

上面考虑了第一极小值的情况。可以仿照上面的方法，将狭缝均分为4段、6段、8段…… 2 n {\displaystyle 2n} 段，则 n {\displaystyle n} 级衍射极小值位置的衍射角满足下面的方程

这里 n {\displaystyle n} 是非零整数，表示第 n {\displaystyle n} 级暗纹（极小值）。

此外，辐照度分布可以由夫琅禾费衍射方程给出：

这里

I ( θ θ --> ) {\displaystyle I(\theta )} 为给定角度位置处的辐照度

I 0 {\displaystyle I_{0}} 初始辐照度

当 x ≠ ≠ --> 0 {\displaystyle x\neq 0} 时， sinc ⁡ ⁡ --> ( x ) = sin ⁡ ⁡ --> ( π π --> x ) / ( π π --> x ) {\displaystyle \operatorname {sinc} (x)=\sin(\pi x)/(\pi x)} ，在原点处 sinc ⁡ ⁡ --> ( 0 ) = 1 {\displaystyle \operatorname {sinc} (0)=1}

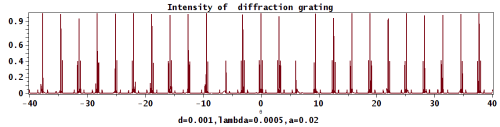
单缝衍射强度分布公式

单缝衍射的强度分布可用下列简单公式表示：

I= sin ⁡ ⁡ --> ( π π --> ∗ ∗ --> d ∗ ∗ --> sin ⁡ ⁡ --> ( ( 1 / 180 ) ∗ ∗ --> p i ∗ ∗ --> θ θ --> ) / λ λ --> ) 2 ∗ ∗ --> λ λ --> 2 ∗ ∗ --> 32400 ( π π --> 2 ∗ ∗ --> d 1 2 ∗ ∗ --> π π --> 2 ∗ ∗ --> θ θ --> 2 ) {\displaystyle {\frac {\sin(\pi *d*\sin((1/180)*pi*\theta )/\lambda )^{2}*\lambda ^{2}*32400}{(\pi ^{2}*d1^{2}*\pi ^{2}*\theta ^{2})}}}

其中 d 为缝隙的宽度，θ 为角度，λ为波长。

夫琅禾费单缝衍射与菲涅尔单缝衍射有明显不同，前者的第一极小值为0，后者不为0.

双缝衍射

当我们讨论双缝干涉时，为了简化问题，常常假设缝的宽度远小于入射光的波长。这样，在观察屏上就可以看到辐照度近似相等的干涉条纹。事实上，在真实的实验并不总能满足上述假设。呈现在观察屏上的亮条纹是中央最亮，两侧亮度逐渐衰减。因此，实际产生的图样是干涉、衍射效应的总和。简单地说，实际双缝实验的条纹，具有理想双缝干涉中条纹的位置，但是辐照度在观察屏上的分布类似单缝衍射中央强、两侧弱的情况。

考虑到衍射效应，实际的双缝干涉图样的辐照度可以用以下公式计算

其中， β β --> = π π --> d λ λ --> sin ⁡ ⁡ --> θ θ --> {\displaystyle \beta ={\frac {\pi d}{\lambda }}\sin \theta } 为干涉因子，源于缝间距为 d {\displaystyle d} 的双缝干涉效应；而 α α --> = π π --> a λ λ --> sin ⁡ ⁡ --> θ θ --> {\displaystyle \alpha ={\frac {\pi a}{\lambda }}\sin \theta } 为衍射因子，源于缝宽为 a {\displaystyle a} 的单缝衍射效应。

上述公式表明，实际的双缝干涉是干涉和衍射的共同效应。如果考虑问题时把缝宽忽略，把入射波考虑成来自少数几个具有相同相位的波源，那么就称看到的现象为“干涉”；如果把入射波考虑成来自同相位的波阵面（缝宽方向的大量点波源），那么就称看到的现象为“衍射”。这样的说法只是为了分析问题方便，事实上二者常常是同时发生的。

衍射光栅

衍射光栅是狭缝按照一定规律分布的光学装置，它能够调整入射光的相位、振幅等属性，使透过它的光发生衍射、干涉，以达到所需的实验目的。光穿过衍射光栅后形成的图样形状与光栅的结构和数量都有关系。

所有衍射光栅的 m {\displaystyle m} 级极大衍射角 θ θ --> m {\displaystyle \theta _{m}} 满足下列光栅方程

这里

θ θ --> i {\displaystyle \theta _{i}} i 为光波入射到光栅的角度，如果是垂直入射到平面光栅，则 sin ⁡ ⁡ --> θ θ --> i = 0 {\displaystyle \sin {\theta _{i}}=0}

d {\displaystyle d} 为光栅刻线的间距，也成为光栅常数

m {\displaystyle m} 为非零整数

衍射光栅后面给定位置的光波，是衍射光栅诸狭缝衍射光的叠加。用于分离白光中不同频率成分光的分光计，就利用了衍射光栅的原理。

下面位于中间的这幅图显示了具有相同缝间距的双缝光栅和五缝光栅的衍射图样。可以看出，衍射光加强点的位置是相同的，但是光斑的宽度有所不同。

红色激光通过衍射光栅所产生的衍射。

红色激光的多缝衍射图样，上方所示的是2条狭缝的情况，下方为5条狭缝的情况。

波长为633纳米的激光通过一个具有150条狭缝的网格

衍射光栅强度分布

衍射光栅的强度分布是衍射因子和干涉因子的乘积：

P = D ( θ θ --> ) ∗ ∗ --> I ( θ θ --> ) {\displaystyle P=D(\theta )*I(\theta )}

其中 D 是 衍射因子

D = sin ⁡ ⁡ --> ( π π --> ∗ ∗ --> d ∗ ∗ --> sin ⁡ ⁡ --> ( θ θ --> ) / λ λ --> ) 2 ∗ ∗ --> λ λ --> 2 ( π π --> 2 ∗ ∗ --> d 2 ∗ ∗ --> sin ⁡ ⁡ --> ( θ θ --> ) 2 ) {\displaystyle D={\frac {\sin(\pi *d*\sin(\theta )/\lambda )^{2}*\lambda ^{2}}{(\pi ^{2}*d^{2}*\sin(\theta )^{2})}}}

I 是干涉因子：

I = sin ⁡ ⁡ --> ( π π --> ∗ ∗ --> a ∗ ∗ --> sin ⁡ ⁡ --> ( θ θ --> ) ∗ ∗ --> N / λ λ --> ) 2 ( N 2 ∗ ∗ --> sin ⁡ ⁡ --> ( π π --> ∗ ∗ --> a ∗ ∗ --> sin ⁡ ⁡ --> ( θ θ --> ) / λ λ --> ) 2 ) {\displaystyle I={\frac {\sin(\pi *a*\sin(\theta )*N/\lambda )^{2}}{(N^{2}*\sin(\pi *a*\sin(\theta )/\lambda )^{2})}}}

圆孔衍射

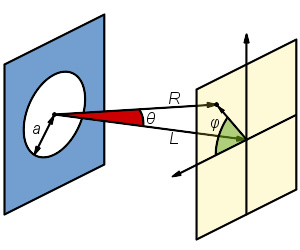
  圆孔衍射的示意图，当 R > a 2 / λ λ --> {\displaystyle R>a^{2}/\lambda } ，即满足远场近似条件时，可以在观察屏上看到衍射图样（艾里斑）。

  电脑模拟生成的圆孔衍射艾里斑图样。

当平面光波入射穿过圆孔时，会形成圆对称的衍射图样，其中心部分最亮，这表示能量主要集中在其零级衍射斑处。上述图样的中心亮斑常被称为艾里斑（ Airy disk ）。 根据远场近似，

式中， a {\displaystyle a} 为环状孔隙的半径， k {\displaystyle k} 为波矢量的大小，等于 2 π π --> / λ λ --> {\displaystyle 2\pi /\lambda } ， J 1 {\displaystyle J_{1}} 为一阶贝塞尔函数。孔隙越小，则给定位置的光斑越大，并且衍射光束偏离原来的传播方向越严重。沿着径向，艾里斑的衍射图样表现为一系列明暗相间的同心圆环，不过径向距离越大，各个明亮圆环的亮度越低。 艾里斑对光学仪器的成像品质有一定的影响。

一般孔隙的情况

从麦克斯韦方程，可以推导出在自由空间里，电场 E {\displaystyle \mathbf {E} } 、磁场 B {\displaystyle \mathbf {B} } 的波动方程：

这里， c {\displaystyle c} 是光速， ϵ ϵ --> 0 {\displaystyle \epsilon _{0}} 是电常数， μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数， ρ ρ --> {\displaystyle \rho } 是电荷密度， J {\displaystyle \mathbf {J} } 是电流密度。

这些方程都具有同样形式的波动方程：

这里， Ψ Ψ --> ( r , t ) {\displaystyle \Psi (\mathbf {r} ,t)} 是描述标量波的波函数， F ( r , t ) {\displaystyle F(\mathbf {r} ,t)} 是波源分布。

假设这波源只发射出频率为 ω ω --> {\displaystyle \omega } 的单色波，

则前述含时波动方程可以写为不含时波动方程：

这里， k = ω ω --> / c {\displaystyle k=\omega /c}波矢是波矢的数值大小， ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 是描述波的不含时波函数， Ψ Ψ --> ( r , t ) = ψ ψ --> ( r ) e − − --> i ω ω --> t {\displaystyle \Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )e^{-i\omega t}} 。

方程 （1） 乃是非齐次亥姆霍兹方程。设 r ^ ^ --> {\displaystyle {\hat {\mathbf {r} }}} 为波的源点，只要能够找到对应的格林函数 G ( r , r ′ ) {\displaystyle G(\mathbf {r} ,\mathbf {r} ")} ，就可以解析这方程。这对应的格林函数必须满足方程

这里， r ′ {\displaystyle \mathbf {r} "} 为任意位置矢量， δ δ --> ( r − − --> r ′ ) {\displaystyle \delta (\mathbf {r} -\mathbf {r} ")} 为三维狄拉克δ函数。

假若找到了对应的格林函数，那么，假若 r {\displaystyle \mathbf {r} } 在积分体积 V {\displaystyle \mathbb {V} } 内，则波函数 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 与格林函数、波源分布的关系式为

格林函数的形式与边界条件有关。对于边界曲面为无穷远的自由空间，格林函数只与 R = r − − --> r ′ {\displaystyle \mathbf {R} =\mathbf {r} -\mathbf {r} "} 有关：

这里， O {\displaystyle \mathbf {O} } 是坐标系的原点。

从这方程，可以观察到，格林函数具球对称性质。因此，采用球坐标，格林函数满足

通过代换，可以得知，形式为射出的球面波的格林函数能够满足以下方程：

注意到，这格林函数假定点波源位于坐标系的原点 O {\displaystyle \mathbf {O} } 。对于空间中任意点波源位置 r ′ {\displaystyle \mathbf {r} "} ，格林函数为

假设波源是在xy-平面的面积分布， f ( r ′ ) = f s ( ρ ρ --> ′ ) δ δ --> ( z ′ ) {\displaystyle f(\mathbf {r} ")=f_{s}({\boldsymbol {\rho }}")\delta (z")} ，那么，

这里， r ′ = ρ ρ --> ′ = ρ ρ --> ′ ρ ρ --> ^ ^ --> {\displaystyle \mathbf {r} "={\boldsymbol {\rho }}"=\rho "{\hat {\boldsymbol {\rho }}}} 为在积分曲面 S {\displaystyle \mathbb {S} } 内的波源位置，以直角坐标表示， ρ ρ --> ′ = ( x ′ , y ′ , 0 ) {\displaystyle {\boldsymbol {\rho }}"=(x",y",0)} ，又 S {\displaystyle \mathbb {S} } 是积分曲面， d σ σ --> ′ {\displaystyle \mathrm {d} \sigma "} 是微小面积分元素， δ δ --> ( z ′ ) {\displaystyle \delta (z")} 是一维狄拉克δ函数。

对于一般的面积分布波源，

根据惠更斯－菲涅耳原理，波前的每一点都是次波的点波源，这些次波共同形成了稍后时刻的叠加波。 假设有波入射于某孔隙，则可以假定这入射波的波前在孔隙内的每一点都是孔隙内的波源，并且推论孔隙内的波源与在同位置的入射波波函数 ψ ψ --> i n c {\displaystyle \psi _{inc}} 有关： f s ( r ′ ) ∝ ∝ --> ψ ψ --> i n c ( r ′ ) {\displaystyle f_{s}(\mathbf {r} ")\propto \psi _{inc}(\mathbf {r} ")} 。虽然这里并没有给出确切关系式，必定存在乘法因子 C {\displaystyle C} ，满足

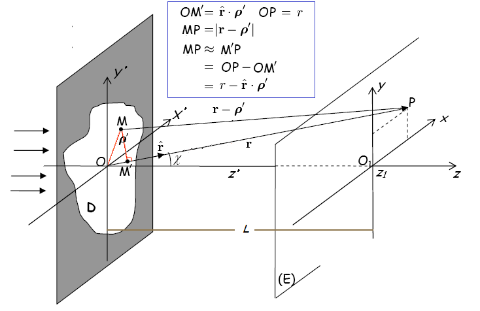
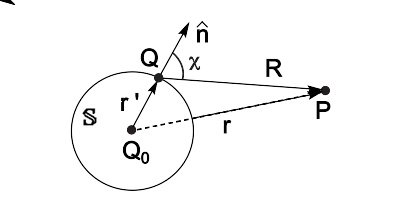
  一般空隙数学推导示意图

假设入射波为平面波， ψ ψ --> i n c ( r ′ ) = E 0 e i k z ′ {\displaystyle \psi _{inc}(\mathbf {r} ")=E_{0}e^{ikz"}} ，孔隙 S {\displaystyle \mathbb {S} } 处于xy-平面，则在孔隙 S {\displaystyle \mathbb {S} } 内，入射波为 ψ ψ --> i n c ( ρ ρ --> ′ ) = E 0 {\displaystyle \psi _{inc}({\boldsymbol {\rho }}")=E_{0}} ，估算的衍射波为

这里，波源位置 ρ ρ --> ′ = ( x ′ , y ′ , 0 ) {\displaystyle {\boldsymbol {\rho }}"=(x",y",0)} 。

假设孔隙是半径为 a {\displaystyle a} 的圆孔，孔心是xy-平面的原点，检验位置是在远场区域， r ≫ ≫ --> a {\displaystyle r\gg a} ，则 | r − − --> ρ ρ --> ′ | {\displaystyle |\mathbf {r} -{\boldsymbol {\rho }}"|} 可以近似为 r − − --> r ^ ^ --> ⋅ ⋅ --> ρ ρ --> ′ {\displaystyle r-{\hat {\mathbf {r} }}\cdot {\boldsymbol {\rho }}"} ，其中 r ^ ^ --> {\displaystyle {\hat {\mathbf {r} }}} 是 r {\displaystyle \mathbf {r} } 的单位矢量。衍射波为

这里， J i ( k a sin ⁡ ⁡ --> θ θ --> ) {\displaystyle J_{i}(ka\sin {\theta })} 是第一类 i {\displaystyle i} 阶贝索函数， r {\displaystyle \mathbf {r} } 的球坐标为 ( r , θ θ --> , ϕ ϕ --> ) {\displaystyle (r,\theta ,\phi )} 。

假射观察屏在远场区域，则照射于观察屏的干涉图样，其邻近中央位置的任意点P与原点 O {\displaystyle \mathbf {O} } 之间的距离 r {\displaystyle r} ，可以近似为观察屏与原点 O {\displaystyle \mathbf {O} } 之间的垂直距离 L {\displaystyle L} ，衍射波在观察屏的辐照度为

这里， I 0 {\displaystyle I_{0}} 是衍射波在干涉图样中央位置的辐照度。

更详细运算，应用格林第二恒等式，可以得到德国物理学者古斯塔夫·基尔霍夫提出的基尔霍夫积分定理的方程

这里， R = r − − --> r ′ {\displaystyle \mathbf {R} =\mathbf {r} -\mathbf {r} "} 是从源位置到检验位置的位移矢量。

激光的衍射

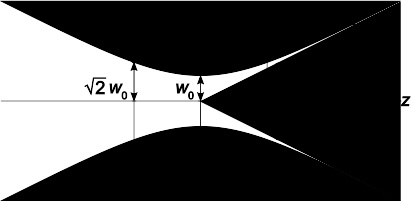
  激光是一种高斯光束（ Gaussian beam ）

激光是一种特殊的可见光，具有极高单色性、定向性、相干性和能量强度。 在理想的情况里，激光束是一种高斯光束。在右边的示意图中，如果定义辐照度在半径为 ω ω --> 0 {\displaystyle \mathbf {\omega _{0}} } 的位置减少为光轴辐照度的 1 / e {\displaystyle 1/e} ，那么距离激光光轴半径为 r {\displaystyle \mathbf {r} } 处的激光场强 E s {\displaystyle \mathbf {E_{s}} } 满足高斯光束（ Gaussian beam ）分布，即

当激光穿过发光系统的镜片后，它的高斯光束参数 ω ω --> 0 {\displaystyle \mathbf {\omega _{0}} } 将发生改变。激光源的输出镜片通常是一个孔隙，因此随后输出的光波形状是由这个孔隙决定。激光束的直径越大，其弯散程度越弱。

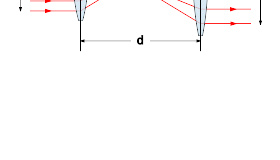
  无焦光学系统可以用来调低激光束的发散。

激光束的发散可以调低。将中央轴同线的两个凸透镜排列在一起，两个凸透镜之间的距离 d {\displaystyle d} 等于它们各自的焦距 f 1 {\displaystyle f_{1}} 、 f 2 {\displaystyle f_{2}} 的代数和：

这种复合透镜组合，前焦距与后焦距都是无穷远，是一种无焦光学系统（ afocal optical system ），由于两个凸透镜的焦点重叠在一起，是一种共焦（ confocal ）双透镜系统。这组合也是开普勒望远镜（ Keplerian telescope ）的基本构造。从前面照射进来的准直光束，通过这复合透镜组合，从后面照射出去也是准直光束，并且截面会增加。这样，可以调低激光束的发散。

另外，使用激光笔等激光器件照射物体时，常常会产生不希望得到的散斑图样（ speckle pattern ）。这是另一种衍射现象。 当激光束照射在粗糙界面上时，由于光束以不同路径传播，不同相位波彼此叠加，会产生振幅、辐照度随机分布的波。

衍射对于光学系统分辨率的制约

在天文学中，通过2.56米孔径望远镜应用幸运成像技术，可以在双星系统的图像中看到双星各自的艾里斑。

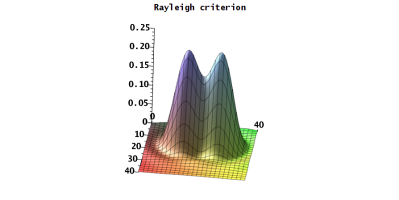
 瑞利判据

光学成像系统的成像质量或多或少都受到衍射的制约。其原因是，入射光在圆形镜片处会发生衍射，形成艾里斑，从而造成光路不能够汇聚到一个点。衍射对成像的影响，主要表现为画面细节模糊不清。在焦平面上，艾里斑的半径为

这里， λ λ --> {\displaystyle \lambda } 为光的波长， N {\displaystyle N} 为光学系统中镜头的焦比（焦距与孔径的相对比值）。对应的分辨角为

其中， D {\displaystyle D} 为光学系统物镜（例如望远镜的主镜片）的尺寸。

给定两个点波源，它们会各自产生艾里图样。当这两个点波源相互越加靠近对方时，两个艾里图样也会慢慢开始重叠，最后甚至会合并形成单一的图样，从而导致无法分辨出两个独立波源所对应的图像。使用望远镜观察太空中的一对双星就很可能遇到这样的情况。瑞利准则指出，只有当两个像之间的距离大于或等于艾里斑的半径时，也就是说，当一个圆斑的中心（中央的主极大值位置）不在另一个圆斑的边缘（第一极小值位置）之内， 才可以说这对应的两个独立波源能够被明确分辨出来。

这样，当镜片孔径越大、波长越短，则光学系统的分辨率越好。这就是望远镜具有大口径镜头的原因。这也解释了显微镜观察细节的能力受到限制的原因。

衍射波的普遍性质

  此图的上半部分显示了氦-氖激光束在一个椭圆孔隙处的衍射图样；下半部分为其二维傅里叶变换，粗略地重现了孔隙的形状。

通过总结各种不同的实验现象，可以发现波的衍射具有以下普遍性质：

衍射波的角间距与造成衍射的物体的尺寸负相关。也就是说，造成衍射的物体的尺寸越小，它所形成的衍射条纹越宽，反之亦然。例如，在单缝衍射里，根据公式 d sin ⁡ ⁡ --> θ θ --> = λ λ --> {\displaystyle d\,\sin \theta =\lambda } ，当入射波的波长 λ λ --> {\displaystyle \lambda } 一定时，狭缝宽度 d {\displaystyle d} 越小，第一极小值对应的 θ θ --> {\displaystyle \theta } 就越大，从而造成中间的亮纹宽度增加；

某一级衍射角的大小，只取决于入射波的波长与衍射物体尺寸的相对比值；

当造成衍射的物体结构具有周期性（例如衍射光栅），则衍射后的图样会变得更窄。例如，对比2条狭缝产生的衍射与5条狭缝产生的衍射，两种情况的狭缝间距相等，不过5条狭缝产生的衍射图样更细（参见衍射光栅一节的第三幅插图）。

粒子衍射

量子理论指出，所有的实物粒子都具有波动性。特别的，大质量粒子可以发生明显的干涉和衍射现象。电子和中子的衍射是量子力学的重要关注对象。根据德布罗意假设，

这里 h {\displaystyle h} 为普朗克常数， p {\displaystyle p} 是实物粒子的动量（低速情况下等于质量和速度的乘积）。

对于大多数宏观粒子来说，它们所具有的德布罗意波长非常短，不足以表现明显的波动性。 例如，以每秒30,000米移动的钠原子，其德布罗意波长大约为50皮米（ pico meter ）。德布罗意在进行论文答辩时让·佩兰曾询问他如何证明他所谓的“物质波”，德布罗意回答说：“用晶体对电子的衍射实验可以做到”。 后来，电子在镍晶体的衍射印证了他的假设。

即便是最小的宏观物体，其波长还是非常小，因此物质波的衍射现象只能在微观的粒子（例如电子、中子、原子和小分子）上体现。这些物质的短波长使得它们很适合用来研究固体和大分子（诸如蛋白质）的原子晶体结构。

一些相对较大的分子，像富勒烯，也能表现出衍射现象。

布拉格衍射

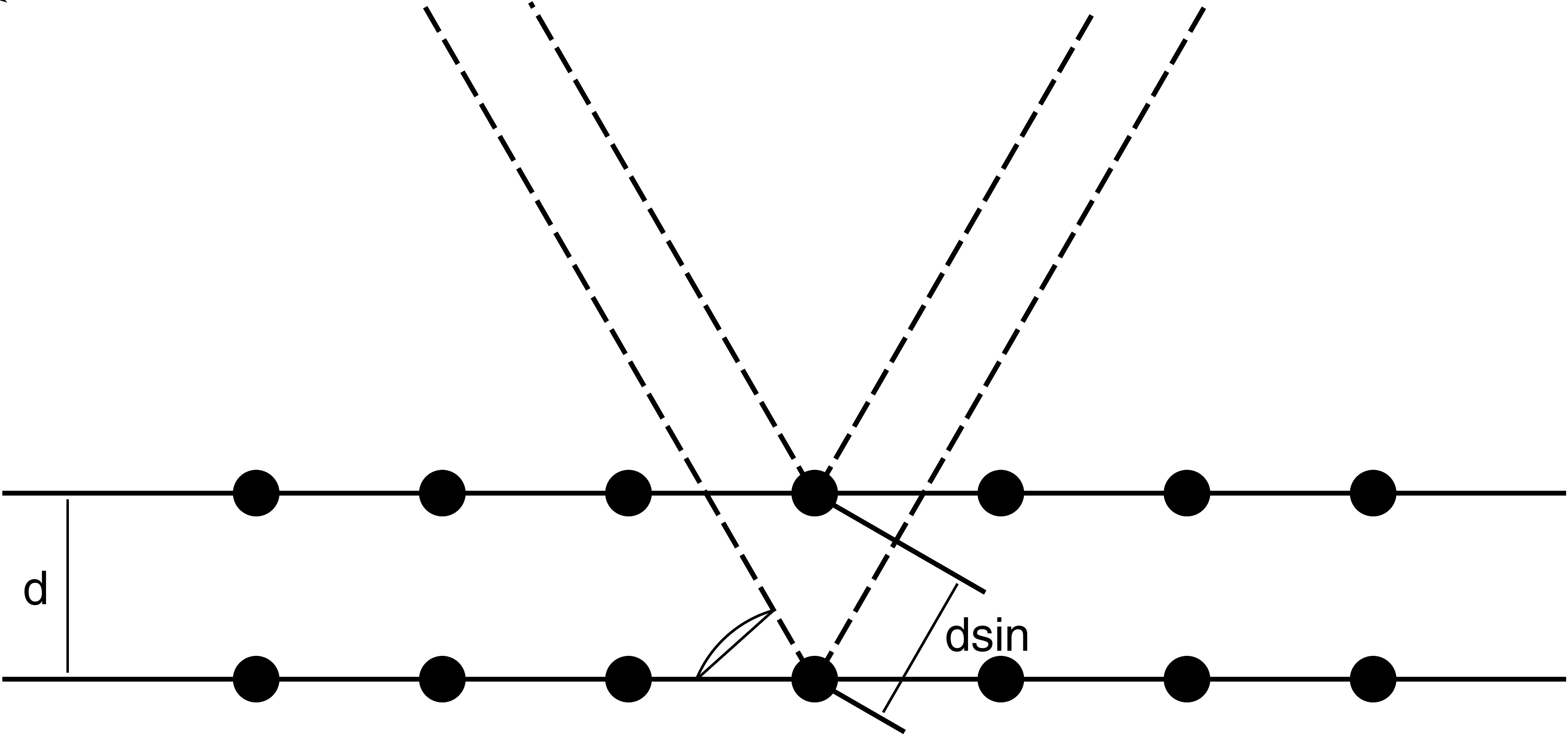
  布拉格衍射示意图：两束具有同一波长和相位的入射波，入射到晶体结构，并被图中的两个原子散射。简单计算可以看出，两束波的传播路径差为 2 d sin ⁡ ⁡ --> θ θ --> {\displaystyle 2d\sin \theta } 。当这一路径差恰好为入射波波长的整数倍时，将会干涉相长，在衍射谱上表现为布拉格尖峰。

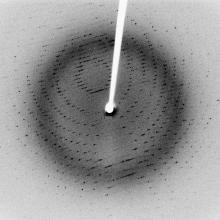
  图示为布拉格衍射的实验图样。根据布拉格定律，衍射图样中的每一点都是由穿过晶体的X射线干涉相长而形成。这项实验的数据可以用来确定材料的晶体结构。

晶体具有周期性的物质结构。由于在这种周期性结构中，原子间距为10 米数量级，因此它可以作为波的衍射光栅。 如果满足一定的条件，就能够使入射波发生衍射现象，这样的衍射被称为布拉格衍射。 它与光波在其他衍射光栅中发生的散射现象类似。同相位的入射波经过不同晶面，在晶格原子处发生衍射后，将会具有相位差，从而产生干涉相长或干涉相消，这就形成了布拉格衍射。若不考虑康普顿散射，则波束的波长在进入晶体前后不发生改变。根据布拉格定律，干涉加强位置所满足的条件为

这里

λ λ --> {\displaystyle \lambda } 为入射波（如常用的X射线等）波长

d {\displaystyle d} 为晶面间距

θ θ --> {\displaystyle \theta } 为衍射角度

m {\displaystyle m} 为衍射级数

晶体学中的布拉格衍射可以利用短波长的波作为入射波。由于X射线的波长与原子间距具有相同的数量级，因此在实验中经常被用作入射波。此外，实验中还经常用到50千伏的电子束，当用电子束进行小角度倾斜入射时，它仅能够穿透大约5纳米的垂直距离，因此主要被用于薄膜材料的观察。而中子因为具有磁矩，常被用来研究磁性材料。 由于这些入射波的波长小于或接近原子的间距，实验可以产生较明显的衍射辐照度分布谱线。 通过测量入射电磁波衍射谱上布拉格尖峰的位置，并利用上面的衍射公式，就可以求得晶面间距 d {\displaystyle d} ，并由此推测晶体的结构。传统的布拉格衍射方法包括劳厄法、旋转单晶法和粉末衍射法等。 由于发现布拉格定律的贡献，威廉·亨利·布拉格及其子威廉·劳伦斯·布拉格获得了1915年的诺贝尔物理学奖。

此外，在电子显微镜或X射线形貌器（ X-ray topography device ）中，衍射衬度（ diffraction contrast ）可以用来检验晶体中的缺陷以及局部应变场（ local strain field ），进行金属薄膜材料的相关研究。

光的相干性

同一波源发射的波，由于传播路径不同，会在观察屏上产生干涉情况。在这种描述里，经过不同路径到达给定点的波之间的相位差只与它们的有效光程有关，而与时间无关。正因为如此，观察屏上给定点的明暗情况是确定的，这样总体上会形成稳定的图样。如果采用不相干入射光，那么其中的不同波传播到给定点时的相位差将会极快地、无规则地变化，这样在观察屏上就无法形成稳定的干涉相长或干涉相消的图样，而是在这两种情况之间不断变化，以至于无法观察到明暗条纹。

一束光波的相位在某段长度上是相关的，这段长度被称作是纵向相干长度，简称为“相干长度”。为了使干涉能够发生，光程差必须小于相干长度。有时候，这被称为波谱相干性，因为它与波中存在的不同频率成分有关。在原子跃迁发射光波的情况中，相干长度与原子产生跃迁的激发态的寿命有关。

如果光波由扩展光源发射，则可能会出现横向的不相干。当观察一束光的截面时，相位在某段横向距离上是相关的，这段横向距离被称作是“横向相干长度”。在杨氏双缝实验中，这意味着如果横向相干长度比两条狭缝的间距小，那么在观察屏上形成的图样看起来就像是两个独立单缝形成的衍射图样。

在电子、中子和原子等离子的情况中，相干长度与描述粒子的波函数的空间范围有关。

参见

衍射的数学表述（ diffraction formalism ）

衍射的动力理论（ dynamical theory of diffraction ）

激光衍射分析（ Laser diffraction analysis ）

衍射仪（ diffractometer ）

大气层衍射（ atmostpheric diffraction ）

光环

彩云

X光散射技术

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。