光速-族谱新闻-族谱网

光速

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:690次

转发:0次

评论:0

数值、记法及单位真空中的光速通常以小写c表示，即英文中“constant”（恒等、常数）或拉丁文“celeritas”（迅捷）的首字母。最初，人们曾以詹姆斯·克拉克·麦克斯韦于1865年使用的符号V表示光速。1856年，威廉·爱德华·韦伯和鲁道夫·科尔劳施曾使用c代表另一个常数。该常数后来被证明为光速的√2倍。1894年，保罗·德鲁德重新将c定义为光速。阿尔伯特·爱因斯坦在1905年发表有关狭义相对论的最早德文论文中使用了V，但在1907年便转用当时已通用的符号c。在某些情况下，c表示任何媒介中波传播的速度，而c0则表示光在真空中的速度。这种使用下标的记法受SI官方出版物认可，且与其它相关常数的记法相符，包括真空磁导率μ0、真空电容率ε0（又称电常数）以及自由空间阻抗Z0。本条目以c代表真空中的光速。自1983年起，国际单位制（SI）将米定义为⁄299,792,458秒内光在真空中所运行的...

数值、记法及单位

真空中的光速通常以小写 c 表示，即英文中“ constant ”（恒等、常数）或拉丁文“ celeritas ”（迅捷）的首字母。最初，人们曾以詹姆斯·克拉克·麦克斯韦于1865年使用的符号 V 表示光速。1856年，威廉·爱德华·韦伯和鲁道夫·科尔劳施曾使用 c 代表另一个常数。该常数后来被证明为光速的 √ 2 倍。1894年，保罗·德鲁德重新将 c 定义为光速。阿尔伯特·爱因斯坦在1905年发表有关狭义相对论的最早德文论文中使用了 V ，但在1907年便转用当时已通用的符号 c 。

在某些情况下， c 表示任何媒介中波传播的速度，而 c 0 则表示光在真空中的速度。这种使用下标的记法受SI官方出版物认可，且与其它相关常数的记法相符，包括真空磁导率 μ 0 、真空电容率 ε 0 （又称电常数）以及自由空间阻抗 Z 0 。本条目以 c 代表真空中的光速。

自1983年起，国际单位制（ SI ）将米定义为 ⁄ 299,792,458 秒内光在真空中所运行的距离。因此，光速的精确值等于 299,792,458 m/s 。光速是一个具有量纲的物理常数，因此 c 的数值取决于所用的单位制。在相对论等经常用到 c 的物理学范畴中，不少文献会使用自然单位制或几何化单位制。在这些单位制中， c = 1 。这样，公式和计算当中就不会出现 c ，因为乘以或者除以1并不会对结果有任何的影响。

在物理学中的基础地位

光在真空中的传播速度独立于波源的运动及观测者的惯性参考系。在麦克斯韦电磁理论的推进下，再加上无法证明以太的存在，爱因斯坦于1905年首次提出“光速不变”这一公设。自此，这一假设已被众多实验充分地证实了。实验只能验证“双向光速”（如：从光源至一面镜子，再回到光源）是独立于参考系的，但若要测量“单向光速”（如：从光源至某个遥远的探测器），就必须先设置光源和探测器时钟之间的同步化规则。如果选用爱因斯坦同步化规则，单向光速就会按照定义等同于双向光速。狭义相对论就是基于光速不变原理所得出的理论。它的另一个公设为：所有惯性参考系都拥有相同的物理定律。其中一项结果，就是所有无质量粒子和相对应的波在真空中都以这一速度 c 运行和传播，这也包括光波。

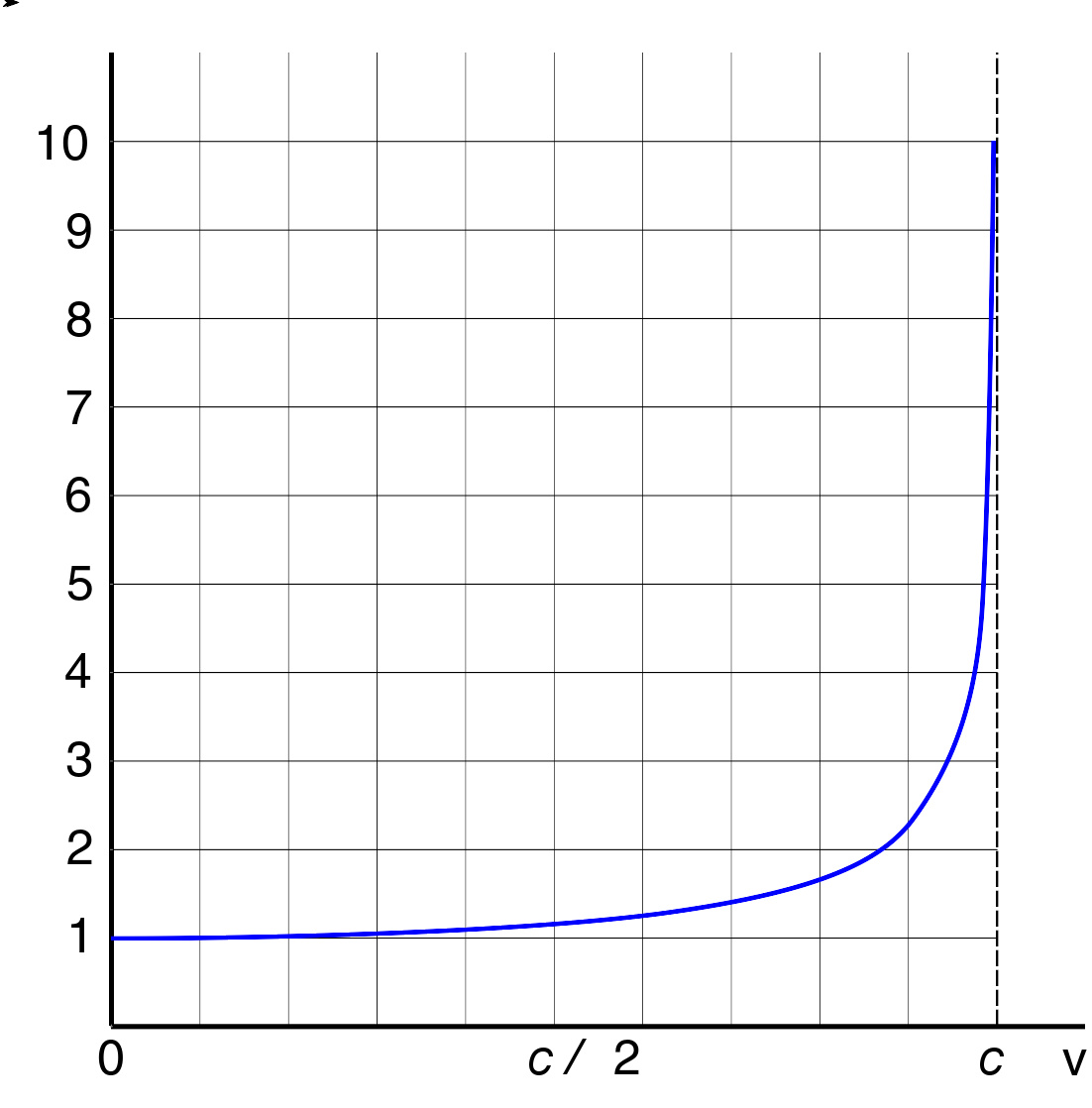
洛伦兹因子 γ 作为速率 v 的函数。因子从1开始，并随着 v 趋向 c 而趋向无限大。

狭义相对论有着不少有悖常理，却有实验证明的结果，例如质能等价（ E = mc ）、长度收缩（运动中的物体长度会缩小）和时间膨胀（运动中的时钟走得更慢）等。长度缩减及时间加长的比率 γ 称为洛伦兹因子，其定义为 γ = (1 − v / c ) ，其中 v 是物体的运动速度。在速度 v 比 c 小很多的情况下（包括大部分日常所见的慢速运动）， γ 很接近1。这时狭义相对论就可以近似为经典力学中的伽利略相对性。然而在 v 非常接近 c 时， γ 趋向无限大，相对论性现象也就会呈现出来了。

要表述狭义相对论的各项结果，可以把时间和空间视为一种综合的结构，即所谓的时空。狭义相对论还要求，所有物理理论均须遵守一种称为洛伦兹协变性的特殊对称性条件。无论是要结合时间和空间，还是要表达这种对称性，在数学公式中都需要 c 这一常数。洛伦兹协变性已几乎成了现今物理理论的必需假设，这些现代理论包括量子电动力学、量子色动力学、粒子物理学标准模型及广义相对论等。故此， c 已成为现代物理学中无处不在的常数，出现在许多与光不相关的领域中。例如，广义相对论预测， c 也是引力波的传播速度。在非惯性参考系中（如受引力扭曲的时空和加速参考系等），“局部”光速是不变的并且等于 c ，但在有限长度内光的运行速度不一定等于 c ，且要视乎该参考系中距离和时间的具体定义。

人们一般假设，诸如 c 等基础常数在整个时空中都具有相同的数值，亦即它不会随地点或时间而变动。（这种“不变性”不同于上文所述的各惯性参考系之间的光速不变性。）不过，有各种理论提倡，光速会随时间改变。目前尚未有确切证据证明光速可变，但对此的研究仍在继续发展。

人们同样假设光速具有各向同性，也就是独立于测量的方向。科学家在不同方向的磁场内对原子核的核能级发射光谱进行测量（对钟实验），又对旋转光共振器进行观测（见迈克耳孙－莫雷实验），所得结果已对光速的各向异性设下了非常严格的上限。

速度上限

根据狭义相对论，一个静止质量为 m 、速度为 v 的物体含有能量 γmc ，其中 γ 为上文定义的洛伦兹因子。当 v 为零的时候， γ 等于1，这就得出广为人知的质能等价公式 E = mc 。当 v 接近 c 时， γ 因子趋向无限大，所以需要无限大的能量才能把该物体加速到光速。光速也就是具有质量的物体的速度上限。这已经得到了众多相对论能量动量实验的证实。

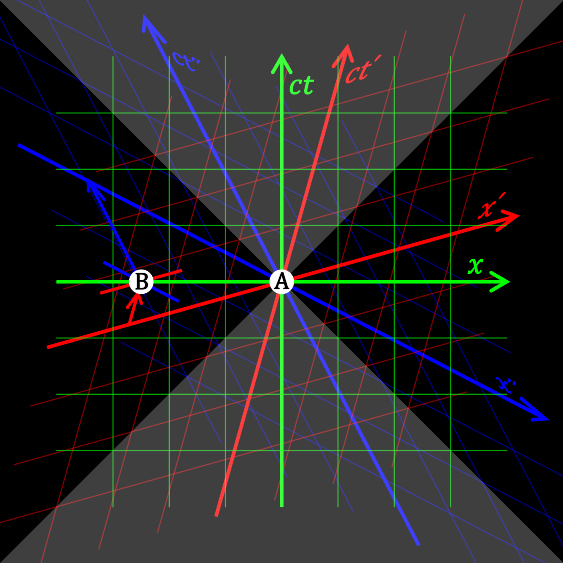
在红色参考系中，事件A发生在事件B之前；在绿色参考系中，两者同时发生；在蓝色参考系中，A发生在B之后。

在正常情况下，消息和能量的传递速度都不可能高于 c 。其中一个论证的方法来自于狭义相对论中“同时”的相对性。这一违反直觉的效应指出，如果事件甲和事件乙之间的距离大于两者的时间间隔乘以 c （即任何低于光速的消息都无法把两个事件联系起来），那么就存在着甲乙发生先后次序不同的三个参考系：一个会测得甲发生在乙之前，一个测得两者同时发生，一个则测得甲发生在乙之后。因此，一旦消息在某个惯性参考系中的传递速度超过 c ，另一个参考系便会观测到它倒著时间逆行，这将会违反因果关系。在这样的参考系里，某“作用”会在其“起因”之前发生。如此的情况从未被观察到，若发生的话则会引致类似快子电话等的佯谬。

超光速观测与实验

更多资料：超光速运动

有时候，物质、能量或消息似乎会超光速运行，但这只是一种错觉。例如，下文将会讲述一些波在媒介中的速度可超过 c 。X射线的相速度在大部分玻璃中都高于 c ，但这一速率并不是波传递消息的速率。

如果把激光束快速扫过一个遥远的物体，这一光点的移动速度可以高于 c 。然而，真正在移动的物体只有激光器和它所发出的光子，而这些光子从激光器离开后，以光速射向远处物体的各个部位。同样，落在遥远物体上的阴影也可以超光速移动。在这些情况下，物质、能量和消息都没有超光速运行。

如果有两个物体都在相对某个参考系移动，它们之间距离的改变速率可以超过 c 。但在任何参考系中，单个物体的速度并没有超过 c 。

一些量子效应显得可以超光速瞬时传递，如爱因斯坦-波多尔斯基-罗森佯谬。两个粒子的量子态可以纠缠起来。在任一个粒子被观测之前，两者的量子态都分别处于叠加的状态。如果把两个粒子分离开来，再对其中一个的量子态进行测量，就可立刻知道另一个粒子的量子态。有关第二个粒子量子态的消息似乎以超过光速的速度抵达观测者。不过，由于无法在一开始控制第一个粒子的量子态，所以还是没有办法利用这一现象来超光速传递消息。

哈特曼效应（ Hartman effect ）也是一种预测超光速运动的量子效应：在特定条件下，一个虚粒子进行量子隧穿的时间会独立于障壁厚度。这时，只要障壁的厚度足够大，虚粒子就能超光速越过这一障碍。但同样地，这一现象是无法用来传递消息的。

在天文观测上，一些天体的视运动速度会超过光速，如射电星系和类星体的相对论性喷流。不过，这类喷流的实际运动速度并没有超过光速：当天体接近光速运行，且其运动方向与视线的夹角小的时候，就会在视觉上产生超光速运动的效果。喷流一开始所发出的光需时更久才到达地球，而稍后发出的光则需时较短。因此在地球观测这两束光的时间间隔比它们实际发出的时间间隔更短，喷流的速度也就显得更高。

在描述宇宙膨胀的模型中，星系之间的距离越大，相互远离的速率亦越高。如果两个星系相隔足够远，它们远离对方的速度就可以超过光速。例如，星系退离地球的速度与它的距离成正比。在所谓的哈勃球边缘以外，天体的退离速度会比光速更高。但是，这种远离的现象并不是因为天体在相对于空间运动，而是空间自身的膨胀所致。

光的传播

在经典物理学中，光是一种电磁波。电磁场的经典物理性质由麦克斯韦方程组所描述，其中电磁波在真空中就以速度 c 传播。常数 c 与电常数 ε 0 和磁常数 μ 0 有以下的关系： c = 1/ √ ε 0 μ 0 。在现代量子物理学中，电磁场由量子电动力学（QED）描述。QED理论中的光是电磁场中的最基本激发态（量子），又称光子。光子不具质量，因此根据狭义相对论，它们在真空中必须以光速运行。

QED的一些延伸理论主张光子具有非零的质量。其运行速度取决于光的频率，而狭义相对论的常数 c 就成了光子在真空中运行的速度上限。严谨的实验从未探测出光的速度随频率的变化，这为光子的质量设下了严格的质量上限。这一上限的具体数值要视乎所用的模型：若带质量光子是由普洛卡理论（ Proca theory ）描述的，实验所得的质量上限就是10 克；若用于描述的是希格斯机制，上限就会较为宽松： m ≤ 10 eV/c 2 （约2 × 10 g）。

另一个提倡光速随频率改变的原因是，狭义相对论无法像某些量子引力理论推测的那样，能应用到任意小的尺度上。2009年，科学家在测量了GRB 090510伽马射线暴的光谱之后，并没有发现不同能量的光子有不同的速度。这意味着，洛伦兹不变性至少准确至普朗克长度（ l P = √ ħG/ c ≈ 1.6163 × 10 m ）除以1.2。

媒介

在媒介中，光的传播速度一般不等于 c ，不同类型的光波也会以不同的速度传播。平面波（充斥整个空间，并只有一个频率）的单个波峰和波谷的前进速度称为相速度 v p 。实际的有限信号（光脉冲）则会以不同的速度传播。脉冲的最大部分以群速度 v g 前进，而脉冲的最前部分则以波前速度 v f 前进。

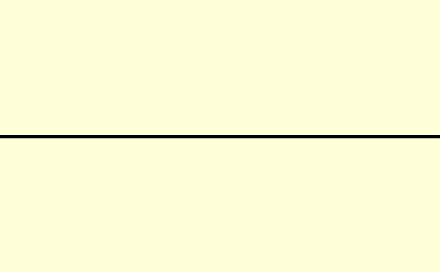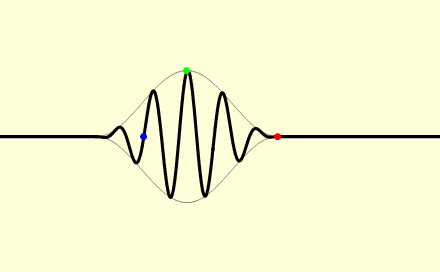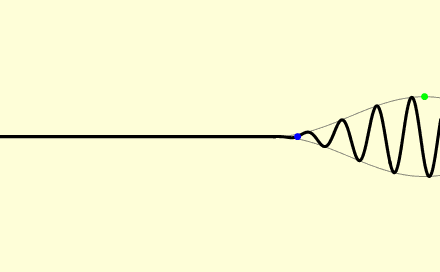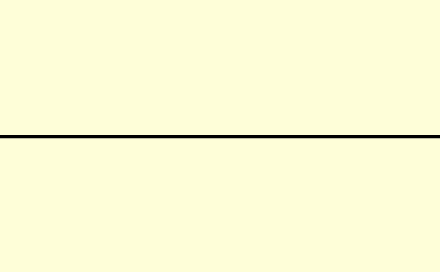
蓝点随着单个波峰和波谷移动（相速度），绿点随波的包络最大位置移动（群速度），红点则随脉冲的最前端移动（波前速度）

相速度会决定光如何穿过一个媒介，或如何从一个媒介跨越到另一个媒介中。这一速度通常以所谓的折射率来表示：一个媒介的折射率是 c 与相速度 v p 之比。折射率越高，相速度就越低。单一物质的折射率可受光的频率、强度、偏振、传播方向等的影响，不过通常可以假设折射率是一个只取决于物质属性的常数。空气的折射率约为1.0003。密度更高的介质则具有更高的折射率：液态水、玻璃和钻石的折射率分别为1.3、1.5和2.4（可见光频段）。在奇异材料中，例如接近绝对零度的玻色–爱因斯坦凝聚，光可以降速至每秒数米的速度。然而，光在媒介中的降速，纯粹是因为光在原子间被吸收后再辐射的延时效果所造成的。以下是一个更极端的“光降速”的例子。美国麻省剑桥的两个物理小组独立研究，两者都利用铷的玻色–爱因斯坦凝聚使光在其中“完全停止”。不过，在这一现象中，光只是被暂时存储在原子的激发态中，在另一激光脉冲的激发下，随时可重新发射出来。在被停顿的那一段时间内，原来的光并不处于光的状态。所有透明材料使光降速的现象，在微观尺度下的原理都和以上的例子相似。

透明材料的折射率一般高于1，代表相速度低于 c 。但某些频率的光在某些材料中的折射率可以低于1，有时甚至可低于零（负折射率）。然而正如上文所述，因果关系是不可违反的，所以任何物质的介电常数的实部和虚部──分别对应于折射率和衰减系数──必须遵守克拉莫-克若尼关系式。简单地来说，如果材料的折射率低于1，波就会在其中被迅速吸收，使得消息不可能以超过 c 的速度传递。

如果组成脉冲的各个频率有不同的相速度，那么脉冲的相速度和群速度就会不同，而且会随时间摊开变平，这一现象称为色散。一些材料的光波群速度特别低（甚至等于零），这种情况称为慢光。许多实验都能够证实这种现象的发生。另一方面，也有实验证明相反现象的存在：群速度超过 c 。理论上，群速度甚至有可能无限大，即脉冲瞬时传播；或是负数，即脉冲随时间反向行进。

这些情况都无法用来超光速传递消息，因为消息速度永远低于脉冲最前端的速度（波前速度）。可以证明，波前速度（在特定情况下）的确等于 c 。

粒子在介质中的运动速度可以超过光在其中的相速度（但仍低于 c ）。当带电粒子在介电质中的运动速度超过光的相速度，它就会发射出类似激波的切连科夫辐射。

光速有限在应用上的影响

光速有限在通信方面有重要的意义：单向及来回通信延迟时间不为零。它的影响范围小至电子学，大至天文学。另一方面，光速不变的性质可以用来测量距离。

小尺度

光速为超级电脑中处理器之间数据传输的速度设下了限制。如果处理器的时钟频率为1GHz，那么在一个时钟周期内，信号的发送距离就只有大约30 cm。必须缩减处理器之间的距离，才可避免通信延迟，但这又会使冷却更为困难。不断提升的时钟频率最终甚至会限制单个芯片的内部设计。

地球上的通信

地球赤道周长为 40,075 km ，而 c 大约等于 300,000,000 m/s ，所以信息沿着地球表面需时67毫秒才能行进半个地球的距离。光在光纤中的实际传递时间则会更长，因为光纤内的光速比 c 慢大约35%，具体数值同折射率 n 相关。更甚者，全球性通信很少用到两点之间的最短距离，而且信号在通过电开关和信号再生器时还会加入额外的延时。

航天与天文学

动画显示一束光离开地球，以有限的速度射向月球。假设地月平均距离，光束从地球表面到月球表面需时1.255秒。图中地月系统的相对大小和距离均依照实际比例绘出。

地球与航天器之间的通信无法瞬时传递。有限光速所带来的信号延时会随着距离的增大而变得更明显。当阿波罗8号成为首艘进入月球轨道的载人飞船时，它与地面任务控制中心的通信就有明显的延时：从地面发出的提问至少要等3秒才会得到回复。地球和火星之间的通信延时介乎5到20分钟，具体数字要看当时两者的相对位置。若位于火星表面的机器人遇到问题，地面的控制人员要等5到20分钟才会收到消息，接着发出的指令又要等待5到20分钟才会抵达火星。地面与木星探测器的通信延时高达数小时。一旦发生导航错误并须要人为干预，会有错过时机的危险。

来自其他遥远天体的光和信号需要长得多的时间才能到达地球。例如，哈勃超深空视频中来自极远星系的光，在被探测之前已经过了130亿（13×10 ）年的飞行时间。这些图片所捕捉到的，是这些星系130亿年前的样子，当时的宇宙年龄还不到10亿年。有限的光速使得天文学家能够观察远处天体更年轻时的样貌，从而研究恒星、星系和宇宙的演化。

天文距离有时会以光年作单位，特别是在科普作品和媒体报导之中。一光年等于光在一年的时间内所行进的距离，约等于9.461兆（万亿）千米，又等于0.3066秒差距。比邻星是除太阳以外最接近地球的恒星，其距离地球约4.2光年。

距离测量

雷达系统通过发出无线电波，并测量电波从目标反射回来后的总时间，从而计算目标的距离。目标的距离是来回飞行时间的一半，乘以光速。全球定位系统（ GPS ）接收器通过测量来自各个卫星的电波信号的抵达时间，计算它与这些卫星的距离，再推算接收器在地球上的位置。由于光在一秒内能行进30万千米，所以这些时间的测量必须非常精准。月球激光测距实验、射电天文学和深空网络利用来回飞行时间，分别量度月球、各大行星及航天器的距离。

高频交易

光速在高频交易当中有重要的意义。交易者为了在进行交易时快人一步，已开始在在各交易中心之间使用微波通信，因为光纤内的光速比 c 慢30%至40%，而微波在大气层中的速度则非常接近 c 。

测定

光速 c 的测量方法有若干种。最直接的方法是量度光波行进的实际速度，不同的天文和地面设备都可以这样测定光速。不过，还可以通过测量其他物理常数，再利用物理定律来推算出 c ，例如用ε 0和μ 0与 c 的关系。在历史上，最准确的光速测量方法是分别量度光束的频率和波长，两者相乘后得出 c 。

1983年，国际单位制将米重新定义为“ ⁄ 299,792,458 秒内光在真空中行进的距离”，从此把光速的准确数值设为 299,792,458 m/s （详见下文）。因此，更准确地测量光速将不再提高 c 数值的精度，而是会使“一米”的定义更加准确。

天文测量法

通过观察木星掩食木卫一的时间来判断光速

外太空是测定光速的理想场地，因为它空间大，又处于近乎真空的状态。一般人们会量度光走过太阳系内某个基准距离所需的时间，例如地球轨道半径。过去人们用这种方法测量的光速数值可以较为准确地表达成常用单位，但实际准确度要视乎基准距离的准确度。这样得出的的光速通常以天文单位（ AU ）每天的单位表示。

奥勒·罗默于1676年用天文方法首次对光速进行测定。从地球观测，卫星围绕行星公转的周期在地球向其靠近时会缩短，在地球远离它的时候则会加长。光从彼方到达地球所需的时间，在地球距离该行星（及其卫星）最近时，比两者相距最远时更短，此二距离只差就是地球绕日轨道的直径。光运行时间的差异，就会导致卫星公转周期在观测上的差异。罗默在木星和木卫一系统中观察到这种现象，并依此推断光横跨地球轨道直径需要22分钟的时间。

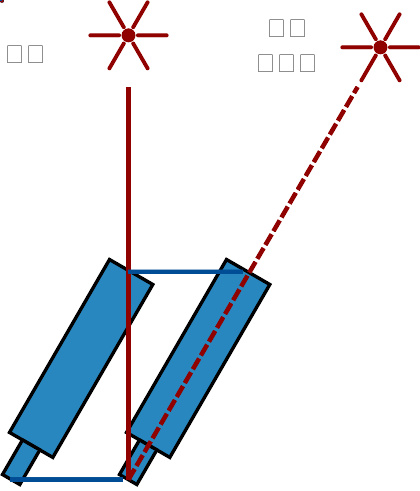
光行差：由于光速有限，来自远处的光会因望远镜的移动而产生视觉上位移。

另一个方法是测量光行差。詹姆斯·布拉德雷于18世纪发现并描述这一现象。光行差现象是来自遥远光源的光束速度与观测者速度的矢量和所致。对于移动中的观测者来说，光源的位置会偏离其实际位置。由于地球绕日公转的速度是连续变化的，所以光行差会使恒星的视位置来回移动。根据恒星在天球上位置的最大角度差（最多达20.5弧秒），可以推算出光速和地球公转速率之间的关系。利用一年的已知时长，就可以换算出光从太阳抵达地球所需时间。1729年，布拉德雷用光行差算出，光速比地球公转速率快10,210倍（实际为10,066倍）。

天文单位

一个天文单位（ AU ）约等于地日平均距离。2012年，国际单位制将天文单位定义为准确值 149,597,870,700 m 。此前，天文单位的定位基础并不是国际单位制，而是在经典力学框架下以太阳所施的引力来表示。目前的定义则用到旧定义时所测量出、以米作为单位的数值。对天文单位的重新定义，和对米的重新定义有相同的意义：从此光速就有了“天文单位每秒”的准确数值（从“米每秒”的准确数值换算出）。

在重新定义之前， c 的倒数，即“秒每天文单位”，可以通过对比无线电信号抵达太阳系各处航天器所需的时间推算而得。用多个数据点绘图，便可得出光运行单位长度所需时间的最佳拟合数值。在2009年，经国际天文联会认可的最佳估值为：

以上数值的相对不确定性为10亿分之0.02（ 2 × 10 ），相等于在地球表面使用干涉测量术测量距离的不确定性。由于米已被定义为光在特定时间内行进的距离，所以在旧定义下以天文单位来表达光速，相当于以米单位来测量天文单位（旧定义）的长度。

飞行时间法

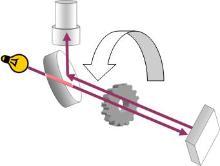
斐索-傅科仪示意图

另一种测定光速的方法是在已知距离外放下一面镜子，再量度光到达镜子反射回来的时间。这是阿曼德·斐索和莱昂·傅科发明的斐索-傅科仪的原理。

斐索把一束光射向8千米以外的一面镜子。在光束的路径上有一个旋转的嵌齿轮。在特定的转速下，光束出去时穿过齿轮的缝隙，回来时又会穿过另一个缝隙。但一旦转速稍微不同，回来的光束就会被轮齿挡住，不能通过。只要知道嵌齿轮和镜子间的距离、轮齿数目及转速，就可计算出光速。

傅科的做法则是用旋转的镜子代替嵌齿轮。由于光在两个方向运行的时候中间的镜子会继续旋转，所以光在出去时和回来时会以不同的角度被中间的镜子反射。只要知道角度之差、镜子的转速和远处镜子的距离，就可算出光速。

今天，利用时间分辨率小于1纳秒的示波器，可以直接量度激光或LED光从镜子反射回来的延时。这种方法的精确度比其他现代测量法低（误差在1%的数量级），但有时会在大学物理课上作演示之用。

电磁常数

麦克斯韦电磁理论将 c 与真空电容率 ε 0 和真空磁导率 μ 0 联系起来： c = 1/( ε 0 μ 0 )。真空电容率可以通过测量已知大小电容器的电容所得；由于安培单位的定义，真空磁导率的准确值被固定在 4π × 10 H·m 。Rosa和Dorsey在1907年用这种方法得出的光速值为 299,710 ± 22 km/h 。

谐振腔

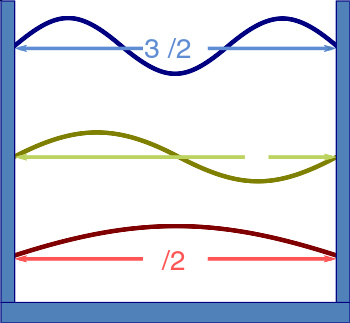
空腔内的电磁驻波

光速还可以通过分别测量光在真空中的频率 f 和波长 λ 而得。两者相乘后就可得出 c 的数值： c = fλ 。其中一种方法是测量空腔谐振器的频率。如果同时亦知道谐振腔的尺寸，就可以算出波长。1946年，路易斯·艾森（ Louis Essen ）和A·C·戈登-史密斯（ A.C. Gordon-Smith ）测量了各种微波正交模在已知尺寸的微波谐振腔内的频率。他们所用的标准尺寸是用干涉法校准的，所量得的谐振腔尺寸准确至约±0.8 μm。运用电磁学理论，可以从谐振腔的形状推算出模态的波长。这就足以算出光速的数值了。

艾森和戈登-史密斯所获取的数值 299,792 ± 9 km/h 比此前用光学方法获取的要准确得多。艾森重复进行测量，到了1950年得出的数值为 299,792.5 ± 3.0 km/h 。

这种方法可以用家居微波炉和棉花糖或牛油等食物来示范。如果把转盘拿走，食物就不会在炉内转动。这时食物在反节点（波幅最高处）的煮熟时间最短，这可以通过观察它的融化过程来判断。两个反节点之间的距离等于波长的一半。若将波长乘以微波的频率（一般在微波炉背部标示，通常是2450 MHz），就可算出光速，误差可以在5%以下。

干涉法

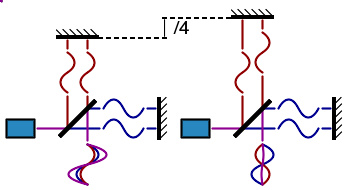
干涉测量法的原理。左：相长干涉；右：相消干涉

干涉测量法也是一种量度光波波长的方法。一束已知频率（ f ）的相干光（如激光）在被分开行走不同路径后重新结合起来。在调整路径长度的同时观察干涉图样，又对路径长度作非常准确的测量，就可以得出波长（ λ ）。计算光速的公式同上： c = λf 。

在激光科技的发明之前，科学家曾使用无线电波进行干涉法来测定光速。然而，波长越长，干涉法所得出的波长数值就越不准确，因此较早获取的数值准确度受到了无线电波长（约0.4 cm）的限制。通过降低电磁波的波长，可以增加准确度，但就增加了直接测量频率的难度。一个解决方法是，先从频率能够准确测得的低频信号开始，再在低频信号的基础上创建更高频信号。这时可以把激光锁定到这一频率，激光的波长就可以用干涉仪得出了。此方法是美国国家标准局（今国家标准技术研究所）的一个小组所发明的。他们在1972年测量光速的不确定性分数为 3.5 × 10 。

历史

一直到近代以前，人们都不知道光是瞬间传递，还是以极快的有限速度传递。对这一问题有记载的最早研究是在古希腊时期。古希腊、世界以及欧洲经典学者都对此进行了长期的讨论，直到罗默首次测出光速，并得出了结论。到了20世纪，爱因斯坦的狭义相对论指出，光的速度无论在任何参考系中都是一样的。自此，科学家对光速的测量数值越来越准确，直到1983年国际单位制对米的重新定义把光速固定为一个准确值。

早期历史

恩培多克勒（前490－前430年）是历史记载中第一个宣称光速有限的人。他相信光是一种运动的东西，所以运行需要时间。亚里士多德却认为，“光是因某物存在所致，而不是一种运动的东西”。欧几里得和托勒密继续发展了恩培多克勒的“发射理论”，即视觉是眼睛发射光线所产生的。根据这一理论，亚历山大港的希罗推论光速一定是无限的，因为睁开眼睛的那一刹那就可以看到遥远的物体。

早期哲学思想和亚里士多德理论一样相信光速无限。1021年，海什木的著作《光学》阐述了一连串推翻发射理论、支持“进入理论”的论据，也就是主张来自物体的光线进入眼睛，产生视觉。海什木因此提出光必定以有限的速度传播，而且光速是可变的──它在密度高的物质内的速度较慢。他又推论，光是一种物质，传递是需要时间的，尽管我们在感官上无法观察得到。同样在11世纪的阿布·拉伊汗·穆罕默德·本·艾哈迈德·比鲁尼也认为光速有限，而且观察到光速比音速快得多。

13世纪的英国科学家罗吉尔·培根在海什木和亚里士多德著作的基础上论述，光在空气中的速度不是无限的。 1270年代，波兰科学家威特罗（ Witelo ）认为，光有可能在真空中以无限的速度传递，要在具有密度的物体中才会降速。

17世纪初，德国科学家约翰内斯·开普勒相信光速是无限的，因为一无所有的空间里没有任何阻碍光线前进的东西。勒内·笛卡儿则论述，如果光速是有限的，太阳、地球和月球在月食之时就会有明显的错位。由于人们从没有观察到这样的错位现象，所以光速是无限的。他甚至认为，如果发现光速是有限的话，他的整套哲学系统可能会因此崩溃。尽管光速是无限的，笛卡儿在对斯涅尔定律的推导当中仍然假设，材料密度较高，其中的光速就越高。皮埃尔·德·费马则支持光速有限的说法，并且在推导斯涅尔定律时用到与笛卡儿相反的假设：介质密度越高，光线的速度就越低。

最早的测定

1629年，荷兰科学家以撒·贝可勒尔曼（ Isaac Beeckman ）提出用肉眼观测大炮的闪光在大约一英里（1.6千米）外一面镜子反射回来，从而计算光速。1638年，意大利科学家伽利略·伽利莱提出一项他声称曾经做过的实验，当中的一方遮掩一盏灯，另一方在一段距离外观察这一动作的延时，再立即遮掩另一盏灯示意。他无法以此辨别光速是有限还是无限的，但他得出的结论是，就算光速是有限的，它也肯定快到不可思议的程度。意大利佛罗伦斯的实验学会（ Accademia del Cimento ）于1667年进行了伽利略的实验。在两盏灯相距约一英里的情况下，没有观察到任何的延时。用今天的已知光速计算，当时的延时只有11微秒。

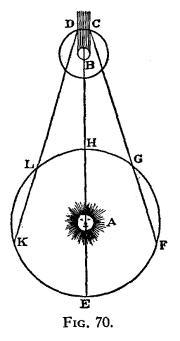
罗默从地球观测木卫一被木星掩食

奥勒·罗默于1676年首次对光速进行测定。他观察到，木卫一绕木星的公转周期在地球靠近木星的时候，比地球远离木星时更短。他从这一点推论光速一定以有限的速度传播，并估算光横跨地球的公转轨道直径需时22分钟。克里斯蒂安·惠更斯利用这一数据，加上对地球轨道直径的估值，计算出光速大约为 220,000 km/h ，比实际数值低了26%。

艾萨克·牛顿在1704年著作《光学》中描述了罗默对光速的计算，并算出光从太阳到达地球需时“七至八分钟”（实际数值为8分钟19秒）。牛顿问道罗默所观察到的掩食阴影有没有颜色，并在得知否定的答案后，得出“不同颜色的光之速度相同”的结论。1729年，詹姆斯·布拉德雷发现恒星光行差的现象。他以此算出，光速比地球公转速度快10,210倍（实际数值为10,066倍），相等于光从太阳到达地球需时8分钟12秒。

与电磁学的关系

阿曼德·斐索在19世纪发明了在地球上进行的“飞行时间测量法”，并得出 315,000 km/h 的光速数值。莱昂·傅科进一步完善了斐索的方法，在1862年所得出的数值为 298,000 km/h 。 1856年，威廉·爱德华·韦伯和鲁道夫·科尔劳施通过莱顿瓶的放电测量出电磁单位荷和静电单位荷之比（1/ √ ε 0 μ 0 ），并发现这与斐索此前所测得的光速非常接近。翌年，古斯塔夫·基尔霍夫算出电信号在无电阻导体中的传递速度也等于此数值。 1860年代初，麦克斯韦在发展电磁理论的时候证明，电磁波在真空中的传播速度相等于韦伯和科尔劳施得出的比值。由于比值和斐索的光速非常相近，麦克斯韦因此提出，光其实是一种电磁波。

以太

亨德里克·洛伦兹（右）和阿尔伯特·爱因斯坦（左）合照

20世纪以前的物理学家曾以为空间充斥着一种称为“以太”的介质，电磁波就在其中传播。一些物理学家把以太视为“绝对静止”的参考系，所以理论上可以通过记录光速的变化来测量地球相对于以太的运动。从1880年代起曾进行了不少旨在探测这种运动的实验，其中最广为人知的要数1887年的迈克耳孙－莫雷实验了。结果显示，相对以太的运动总是比观测不确定性小。更近期的实验指出，双向光速的各向异性（即随观测方向而变化）不大于6纳米每秒。亨德里克·洛伦兹根据这一点，提出仪器在以太中的运动会导致它的自身长度沿着运动方向的收缩，而且移动系统所测量的时间也会随之改变（“局部时间”），这就发展出洛伦兹变换。在洛伦兹以太理论的基础上，昂利·庞加莱于1900年证明，这一局部时间（一阶近似）可以由相对以太移动中的时钟表示，而时钟是在光速不变的假设下同步化的。1904年，他猜测一旦洛伦兹的理论得到证实，光速就有可能是力学上的速度极限。1905年，庞加莱证明洛伦兹以太理论在观测上和相对性原理完全相符。

狭义相对论

1905年，阿尔伯特·爱因斯坦设想，非加速观测者所测得的光速独立于光源及观测者自身的运动。以此作为公设，他继而创建起整套狭义相对论。理论中，真空中的光速 c 是一个基础常数，出现的地方也不仅限于光的传播。物理定律不再需要一个绝对静止的参考系，因此这一举动完全淘汰了当时洛伦兹和庞加莱仍然坚持的以太理论，也大大革新了人们对空间和时间的观念。

光速精确度的提升与米和秒的重新定义

20世纪下半叶，光速的测量准确度随着谐振腔和激光干涉仪的发展而不断地提升。另一方面，更精确的米和秒的定义也陆续被认可。1950年，路易斯·艾森用谐振腔所得出的光速值为 299,792.5 ± 1 km/h 。这在1957年的第12届无线电合会大会上得到采纳。1960年，米被重新定义，基础是氪-86的某个谱线的波长。1967年，秒也被重新定义，基础是铯-133基态的超精细跃迁频率。

1972年，位于美国科罗拉多州波德的国家标准技术研究所利用激光干涉法测定光速，得出 c = 299,792,456.2 ± 1.1 m/s ，其精度比之前的测量高100倍。剩余的不确定性主要来自米定义上的不确定性。由于类似的实验也得出相近的光速值，所以1975年的第15届国际计量大会建议把 299,792,458 m/s 作为光速的数值。

明确固定光速的数值

1983年的第17届国际计量大会结果发现，通过测量频率并固定某一特定光速值所得出的波长比此前的长度单位定义更具有可重复性。大会保留了1967年的秒定义，使铯的超精细频率成为秒和米两个单位的定义基础。米的定义改为：“ ⁄ 299,792,458 秒内光在真空中所运行的距离。” 在这一定义下，光速的准确值就会固定在 299,792,458 m/s ，光速也成了国际单位制所定义的常数之一。在重新定义之前，更准确的测量会使光速值变得更为精确；但在1983年以后，对氪-86以及其他光源的更准确测量不会再改变现有的光速值，而是会增加米单位的精确度。

度量衡大会在2011年表示，整个国际单位制中的七个基本单位都会通过所谓的“明确常数制定方法”来重新定义：“每一个单位都会以明确固定某个广泛认可的基础常数来间接地定义”，也就是米的定义与光速之间的关系。在该提议下，米有了本质完全相同但措辞不同的定义：“米，符号m，是长度的单位；定义为光速在SI单位 m s 下的数值固定为 299,792,458 后，所设置的值。” 这将成为国际单位制的新修订内容之一。

参见

光、电磁波

麦克斯韦方程组

相对论

光速可变理论

超光速

光速不变原理