背景

量子引力与弦

人们现时对引力的理解，是基于阿尔伯特·爱因斯坦的广义相对论 。于1915年成形的广义相对论，是以时间与空间（即时空）的几何来解释引力的理论。它所用的语言是经典物理学 ，是由艾萨克·牛顿及詹姆斯·麦克斯韦等物理学家所开发的。而其他非引力的作用力则由量子力学的框架来解释。量子力学是由二十世纪前半叶多位物理学家所开发的，用概率来描述物理现象，与之前的经典物理学完全不一样 。

探索如何使用量子力学原则来描述引力的物理学分支就是量子引力。现时，最受关注的量子引力手法是弦理论 ，弦理论不使用非零维的点粒子，而改用一维物体──弦来模拟基本粒子。 AdS/CFT 对偶的理论认为量子引力是从弦理论或其现代延伸M理论推导出来 。

人们日常生活中所熟悉的空间有三维（上下、左右及前后），还有一维时间。因此用现代科学的语言，会说时空是四维的 。弦理论和M理论有一个很奇怪的特点，就是时空需要额外的维度，用于维持数学上的一致性。时空在弦理论中有10维，而在M理论中则有11维 。从弦理论或M理论中得出AdS/CFT等量子引力理论的过程，称作紧致化。紧致化能够减低理论的有效时空数，将多余的维度“卷曲”成圆圈 。

紧致化可以通过考虑多维物件来解释，如橡胶水管。如果从足够距离外看橡胶水管的话，它看起来就只有一维，就是长度。然而，向水管靠近的话，就会发现它的第二维圆周。因此在橡胶水管中爬行的蚂蚁能以二维方式移动 。

量子场论

一些物体具有时间空间范围，如电磁场等，而应用在这些物体上的量子力学就是量子场论 。量子场论是粒子物理学研究基本粒子的基础理论，而其中这些粒子是由基本场的激发所描述。而凝聚态物理学也会使用量子场论来模拟类似于粒子的准粒子 。

使用 AdS/CFT 对偶时，除了要考虑量子引力理论外，还需要考虑某一种叫共形场论的量子场论。它是一种对称性强且具有良态的量子场论 。这种理论包括两种应用，一是弦理论，用于描述弦传播时所扫出的表面；二是统计力学，用于模拟热力学临界点 。

对偶概述

由三角形和正方形在 双曲平面 （ 英语 ： Hyperbolic space ） 上的密铺。

反德西特空间的几何

在 AdS/CFT 对偶中要考虑的是在反德西特背景上的弦理论或M理论。亦即是说其空间几何是由爱因斯坦方程的某种 真空解 （ 英语 ： vacuum solution ） 所描述 。

非常基本地来说，反德西特空间是一个数学模型，其中点与点间的距离概念（度规），与日常欧几里德几何中的距离概念不一样。反德西特空间与 双曲空间 （ 英语 ： Hyperbolic space ） 有着密切的关系，而双曲空间可用右图的圆盘表示 。右图为由三角形和正方形所组成的密铺。用某种方式可以为点间的距离下定义，使得所有三角形和正方形都是一样大小的，并且圆周的外边界与其内部任一点的距离为无限 。

现在想像一叠双曲圆盘，其中每一片圆盘代表某时间的宇宙态。而由此形成的几何物体就是反德西特空间 。它看起来像实心的圆柱体，其中每一片截面都是双曲圆盘。下图中时间以垂直方向行进。这圆柱体的表面在 AdS/CFT 对偶中有着重要的角色。反德西特空间跟双曲圆盘一样，它的弯曲方式使得内部任何一点与边界面的距离为无限远 。

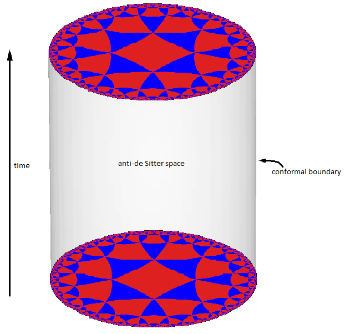
三维的反德西特空间就像是一叠双曲圆盘，每一片圆盘代表某时间的宇宙态。而由此形成的时空看起来就跟圆柱体很像。

这样的结构虽然描述了只有二维空间加一维时间的假想宇宙，但还是可推广至适用于任何维数。双曲空间实际上是可以超过二维的，把这些双曲空间叠起来就能形成反德特空间的高维度模型 。

AdS/CFT的观点

反德西特空间的重要特点在于其边界（三维德西特空间的边界看起来像圆柱体）。这种边界有一个特性，就是在任何点的局部范围都和闵可夫斯基时空很像，而闵可夫斯基时空就是非引力物理所用的时空模型 。

因此可以构建一套“时空”由反德西特空间边界提供的辅助理论。而这项观察正是 AdS/CFT 对偶的起点，因为 AdS/CFT 对偶把反德西特空间的边界视为共形场论的“时空”。对偶主张共形场论相等于反德西特空间主体的引力理论，也就是说两者可以像有“字典”的那样将计算互相翻译。一套理论中的每一件实体在另一套理论中都有对应的实体。比方说，引力理论中的单一粒子可能对应边界理论中的某堆粒子。此外，两套理论的量化预测也是一致的，例如说引力理论中两个粒子碰撞的概率是40%，那么共形场论的对应粒子堆碰撞概率也会是40% 。

图为一幅二维全息图，当中储存了所代表物体的三维信息。上下两幅图画为从不同角度拍摄的同一张全息图。

要注意的是，反德西特空间边界的维度比反德西特空间本身的要低。比方说，上文的三维例子，其边界为二维表面。由于两理论间的关系就像三维物件与全息图形象的关系，所以 AdS/CFT 对偶是一种“全息对偶” 。虽然全息图是二维的，但是它储存了所代表物体的三维信息编码。 AdS/CFT 对偶也是一样，虽然它所联系的两套理论存在于不同维数的时空，但是对偶假定它们是 完全 相等的。共形场论就像是全息图，捕捉了较高维数的量子引力理论信息 。

对偶例子

自1997年马尔达西那发表了他的观察以来，理论物理学家发现了不少 AdS/CFT 对偶的各样实践。它们把各种共形场论与各种维数的弦理论和M理论紧致化联系起来。尽管一般来说要使用这些理论来模拟真实世界并不可行，但是它们却具有一些对解决量子场论和引力难题有用的特点，例如所含有的粒子和高度的对称性 。

AdS/CFT 对偶最有名的例子，就是 A d S 5 × × --> S 5 {\displaystyle AdS_{5}\times S^{5}} 积空间上的IIB型弦理论是相等于四维边界上的 N=4超对称杨-米尔斯理论 （ 英语 ： N = 4 supersymmetric Yang–Mills theory ） 在这个例子中，引力理论所处的时空实际上为五维（因此标记为 A d S 5 {\displaystyle AdS_{5}} ），另外还带有五维的紧空间（由 S 5 {\displaystyle S_{5}} 因子所代表）。至少在宏观角度上，真实世界中的时空为四维，因此这个版本的对偶并不能真实地模拟引力。同样地，由于对偶理论假定大量的超对称性，因此也不适合模拟任何的真实世界系统。然而，如下文所解释，这种边界理论的一些强相互作用互作用的基础理论量子色动力学一致。其所描述的粒子与量子色动力学的胶子类似，同时还描述了某些费米子 。因此，这种理论能应用于核物理，尤其是用夸克-胶子等离子体离子体 。

这项对偶的另一种实践，为 A d S 7 × × --> S 4 {\displaystyle AdS_{7}\times S^{4}} 上的M理论相等于六维时空上的 (2,0)理论 （ 英语 ： 6D (2,0) superconformal field theory ） 。在这个例子中，引力理论的时空实际上为七维。出现在此对偶一端的(2,0)理论，其存在由 超共形场论 （ 英语 ： Superconformal algebra ） 的分类所预测。由于(2,0)理论是一种没有经典极限的量子力学理论，所以物理学家对它仍然缺乏理解 。尽管研究这种理论有其固有的难度，但是从数学与物理的各种理由出发，它还是一个相当有意思的研究课题 。

这项对偶的又一种实践，为 A d S 4 × × --> S 7 {\displaystyle AdS_{4}\times S^{7}} 上的M理论相等于三维的 ABJM超共形场论 （ 英语 ： ABJM superconformal field theory ） 。这里的引力理论有四维的非紧化时空，因此这个版本的对偶能提供某程度上比较真实的引力理论 。

对量子引力的应用

弦理论的非摄动表述

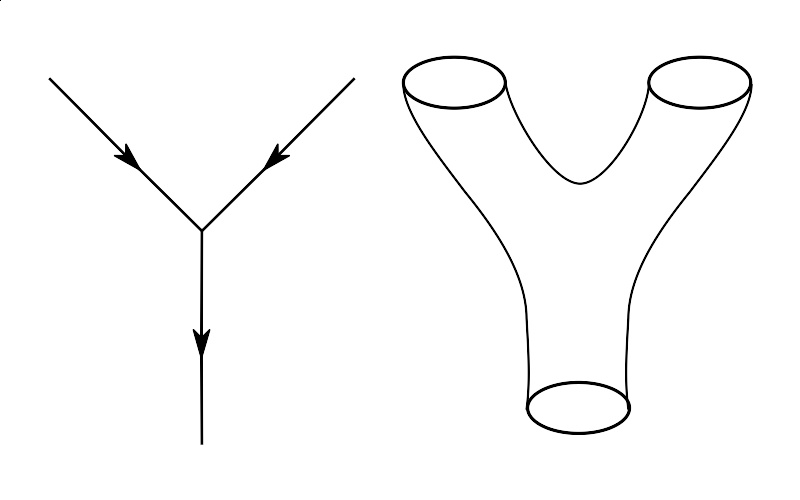
量子世界里的相互作用：点粒子的世界线（左）或由弦理论的闭弦所扫出的 世界面 （ 英语 ： Worldsheet ） （右）。

使用量子场论计算各种物理事件的概率时，一般需要用到摄动理论。摄动量子场论由理查德·费曼及其他物理学家于二十世纪前半叶开发，这项理论使用费曼图来整理计算。费曼图所代表的是点粒子的路径与相互作用 。尽管这种体系对于预测而言非常有用，但是这些预测只能在相互作用强度（由耦合常数所描述）足够小的时候才有效，即摄动理论只能描述弱到近乎不存在的相互作用 。

弦理论的起点在于量子场论的点粒子可由一维的弦的所描述。弦的相互作用有着最直接的定义，可由量子场论的摄动理论推广所得。若从费曼图的视点出发，则意味着把代表点粒子路径的一维图，换成代表弦运动的二维表面（见右图）。跟量子场论不同的是，弦理论并未有全面的非摄动定义，因此弦理论还是不能解答许多物理学家想问的问题 。

研究 AdS/CFT 对偶的其中一个最初动机，就是解决开发弦理论非摄动表述这道难题 。如上文所解释， AdS/CFT 对偶为量子场论的几种例子提供了等价的反德西特空间弦理论。对于引力场为渐近反德西特的特例（即在无限远时引力场类似于反德西特空间上的），这种对偶可被视为给出弦论的 定义 。弦理论中受关注的物理量的定义皆由对偶量子场论的物理量来定义 。

黑洞信息佯谬

史蒂芬·霍金于1975年发表了一份计算，指出黑洞并非全黑，还是会射出暗淡辐射的，而成因则为事件视界附近的量子效应 。由于起初霍金的结果指出黑洞会催毁信息，因此成了理论界的难题。霍金的计算更精确地来说是违反了一条量子力学的基本假想，即物理系统的时间演化需遵守薛定谔方程。这项特性一般被称为时间演化的幺正性。霍金的计算与量子力学幺正性假想间的表面冲突，后来被称为黑洞信息佯谬 。

AdS/CFT 对偶在某程度上成功解决了黑洞信息佯谬，因为它能表明黑洞的时间演化是如何能在某程度上遵行量子力学。用 AdS/CFT 对偶的内容来考虑黑洞是确实可行的，任何此类黑洞都对应一系列位处反德西特空间边缘的粒子 。这些粒子正常地遵从量子力学的规则，特别是幺正性时间演化，因此黑洞也必须符合幺正性时间演化，遵守量子力学的规则 。霍金于2005年承认佯谬以 AdS/CFT 所得的信息守恒告终，并提出了一个黑洞是如何保存信息的具体可行机制 。

对量子场论的应用

核物理

其中一个被 AdS/CFT 对偶研究过的 物理系统 （ 英语 ： Physical system ） 就是夸克-胶子等离子体，它是由粒子加速器所产生的一种奇异物质状态。当如金或铅核等重离子在短暂的瞬间以高能量对撞时会产生这种状态。如此的碰撞使得组成原子核的夸克 退禁闭 （ 英语 ： Deconfinement ） ，而退禁闭时温度约为二万亿开尔文，情况与大爆炸后 10 − − --> 11 {\displaystyle 10^{-11}} 秒时相若 。

夸克-胶子等离子体的物理由量子色动力学所支配，但这理论在数学上并不能够对付夸克-胶子等离子体的相关难题 。 谭青山 （ 英语 ： Đàm Thanh Sơn ） 与协作者与2005年的一份论文中，成功表明可以使用 AdS/CFT 对偶将难题转成弦理论的语言，来研究夸克-胶子等离子体的某些方面 。谭青山与协作者通过应用 AdS/CFT 对偶，利用五维时空的黑洞来描述夸克-胶子等离子体。计算中证明了夸克-胶子等离子体的两个物理量──剪切黏度 η η --> {\displaystyle \eta } 和熵的体密度 s {\displaystyle s} 两者之间的比值约为常数用常数：

其中 ℏ ℏ --> {\displaystyle \hbar } 为约化普朗克常数， k {\displaystyle k} 则为玻耳兹曼常数 。此外，作者还在论文中推测此通用常数就是多个系统中 η η --> / s {\displaystyle \eta /s} 布鲁克限值。布鲁克黑文国家实验室的 离子对论性重离子对撞机 （ 英语 ： Relativistic Heavy Ion Collider ） 于2008年成功确认了比率的预测值 。

夸克-胶子等离子体的另一重要特点就是在浆中移动的超高能量夸克会在仅仅数飞米的距离内被停止或“冷却”。此现象由 喷流冷却 （ 英语 ： Jet quenching ） 参数 q ^ ^ --> {\displaystyle {\hat {q}}} 所描述，该参数将夸克的能量流失与其浆内运动距离的平方联系起来。基于 AdS/CFT 对偶的计算使得理论物理学家能够估算出 q ^ ^ --> {\displaystyle {\hat {q}}} ，并且所得的计算值与参数的测量值大致吻合，因此间接表明 AdS/CFT 对偶可能有助于更深入的研究 。

凝聚态物理学

图为在高温超导体上悬浮的磁铁。现在的物理学家有使用 AdS/CFT 对偶来研究高温超导现象。

研究凝聚态的实验物理学家在过去的数十年间发现了多种奇异的物质状态，包括超导体和超流体。尽管这些状态由量子场论的框架来描述，但使用标准场论技巧还是很难去解释某些现象。包括 苏比尔·萨克达夫 （ 英语 ： Subir Sachdev ） 在内的一些凝聚态物理学家期望 AdS/CFT 对偶能让使用弦理论语言描述这些系统变得可行，从而可以更深入地研究它们的性质 。

以弦理论方法描述超流体至绝缘体的过渡至今已取得一定的成果。超流体是一种流动时没有摩擦力的中性原子系统。这样的系统一般在实验室中用液态氦制作，但近年实验物理学家开发了新的人工超流体制作方式：将数以万亿计的冷原子倒入十字交叉的激光晶格中。这些原子最初相当于超流体，但当实验者增大激光强度时，原子的活动量下降，并突然过渡成绝缘态。原子在过渡途中会出现反常状态。例如，原子会以一定的速率慢慢停止，而这个速率取决于温度和普朗克常数，后者为量子力学的基础参数，并不会出现在其他相的描述中。这样的表现在近年才从对偶描述中得到解答，在描述中流体的特性以高维度黑洞来描述 。

质疑

不少物理学家都转而采用弦理论方法去对付核物理和凝聚态物理学的难题，而一些研究这些领域的理论物理学家则对 AdS/CFT 对偶是否能成为模拟真实世界系统的工具这一点提出质疑。拉里·麦里兰（ Larry McLerran ）于2006年的夸克物质研讨会中 ，指出 AdS/CFT 对偶中的N=4超对称杨-米尔斯理论与量子色动力学有显著差别，因此将这些方法应用于核物理是件难事。据麦里兰所说：

诺贝尔物理学奖得主菲利普·安德森在致《 今日物理 （ 英语 ： Physics today ） 》杂志的一封信中，也表达了对于 AdS/CFT 对偶的凝聚态应用的近似忧虑，其中写道： 在给《 今日物理 （ 英语 ： Physics today ） 》杂志的一封信中，诺贝尔物理学奖获得者菲利普·安德森写道：

历史与开发

杰拉德·特·胡夫特于1970年研究弦理论及核物理的相似点时得出与 AdS/CFT 对偶相关的结果。

弦理论与核物理

物理学家在很早之前就已经着手研究弦理论与核物理间的关系，而 AdS/CFT 在1997年末的发现就是这方面长年所积累的成果 。实际上，弦理论最初在1960年代末至1970年代初被提出时，是用于描述强子的，强子指的是由强相互作用牵引的次原子粒子，如质子和中子。弦理论把每一种的这些粒子视为弦的不同振荡模式。实验物理学家在1960年代末就已经发现，强子符合某一类的 雷吉轨迹 （ 英语 ： Regge trajectories ） ，这种轨迹的能量平方与其角动量成正比；而后来理论物理学家则指出，从旋转相对论性弦的物理中，会自然地出现如此的关系 。

而另一方面，在把强子视作弦的尝试中发现了多个严重的难题。其中一个就是弦理论中包括无质量且自旋为2的粒子，而在强子物理中尚未有对应的粒子 。这样的粒子所传递的力会有着引力的特性。 乔尔·谢克 （ 英语 ： Joël Scherk ） 和约翰·施瓦茨因此于1974年提出弦理论不是理论物理学家以为的核物理理论，而是量子引力理论 。与此同时，物理学家发现了强子实际上是由夸克所组成的，因此他们放弃了用弦理论的手法研究强子，而改为采用量子色动力学。

夸克在量子色动力学中有一种荷具有三种类型，叫色荷。杰拉德·特·胡夫特于1974年的论文中，以近似量子色动力学的观点来研究弦理论与核物理间的关系，当中所用的色荷数为 N {\displaystyle N} ，而不是三。在这篇论文中，特·胡夫特考虑了当 N {\displaystyle N} 趋向无限时的某个极限，并表明在这个极限时某些量子场论的计算与弦理论的计算类似 。

史蒂芬·霍金于1975年预测黑洞会因量子效应而射出辐射。

黑洞与全息理论

史蒂芬·霍金于1975年发表了一份计算，指出黑洞并非全黑，还是会射出暗淡辐射的，而成因则为事件视界附近的量子效应 。之前雅各布·贝肯斯坦在研究就指出过黑洞熵的定义良好 ，而霍金的研究正是这份研究的后续。霍金的结果最初看起来违反了量子力学的基本假想，即时间演进的幺正性。幺正性假想直觉上所说的是，量子系统并不会因为态与态之间的演进而将信息毁灭。因此，这项表面上旳冲突被称为黑洞信息佯谬 。

李奥纳特·萨斯坎德对开发量子引力中全息原理的初期作出过贡献。

杰拉德·特·胡夫特在后来的1993年撰写了一篇具猜想性的论文，其中以量子引力的观点，重新检视霍金的黑洞热力学研究，结论为围绕黑洞的时空自由度总数与视界的表面积成正比 。这个概念被李奥纳特·萨斯坎德改良及提倡，成就了现时的全息原理 。全息原理及其通过 AdS/CFT 在弦理论中的实践，不单对阐明由霍金的研究延伸出的黑洞奥秘有重大作用，而且也为黑洞信息佯谬提供了一个让专家信服的可能解答 。霍金于2004年承认黑洞确实不违反量子力学 ，他同时亦提出了一个黑洞是如何保存信息的具体可行机制 。

马尔达西那的论文

胡安·马尔达西那于1997年末发表了一篇具里程碑意义的论文，就此触发了 AdS/CFT 这一个研究领域 。据亚历山大·泊里雅科夫的说法，那篇论文就是“开启水闸的研究” 。这个猜想马上就引发了弦理论研究界的浓厚兴趣 ，不久后就有两篇认真检视这个对偶的论文，一篇 史蒂芬·格布瑟 （ 英语 ： Steven Gubser ） 、 伊戈尔·克列巴诺夫 （ 英语 ： Igor Klebanov ） 和亚历山大·泊里雅科夫合著 ，另一篇则由爱德华·威滕所撰写 的论文。这两篇论文使得马尔达西那的猜想更加明确，并成功证明了对偶中的共形场论是位于反德西特空间的边界 。

胡安·马尔达西那最早于1997年末提出 AdS/CFT 对偶。

马尔达西那的对偶中有一项特例，就是 N = 4 {\displaystyle {\mathcal {N}}=4} 超杨-米尔斯理论与五维反德西特空间的弦理论是相等的 ，而杨-米尔斯理论则是一种与量子色动力学相近的规范场论。这个结果有助于厘清特·胡夫特之前有关弦理论与量子色动力学间关系的研究，并把弦理论带回以前作为核物理理论的根源 。

AdS/CFT找到了应用

核物理学家 谭青山 （ 英语 ： Đàm Thanh Sơn ） 在1999年开始了在哥伦比亚大学的工作后，就去探望同在纽约的本科时期友人安德烈·斯塔里内特斯（Andrei Starinets），他当时正在纽约大学攻读弦理论博士学位的 。尽管当时二人并没有合作研究的打算，但是谭青山很快就意识到斯塔里内特斯的 AdS/CFT 计算能厘清夸克-胶子等离子体的一些性质，而夸克-胶子等离子体是重离子在高能碰撞下的产物。谭青山在与斯塔里内特斯和帕维尔·柯夫顿（Pavel Kovtun）的合作下，成功使用 AdS/CFT 对偶计算出夸克-胶子等离子体的一个重要参数 。谭青山后来忆述时说；“为了计算出夸克-胶子等离子体旳剪切黏度数值，我们完全改变了整个计算……我其中一位研究核物理的朋友开玩笑说，我们的论文是弦理论的第一份实用论文 。”

时至今日，物理学家仍继续在量子场论中为 AdS/CFT 对偶发掘新应用 。除了由谭青山及同事所提倡的核物理应用，其他如 苏比尔·萨克达夫 （ 英语 ： Subir Sachdev ） 的凝聚态物理学家已经在使用弦理论方法去研究凝聚态物理学的某些方面。其中一个这方向的重要成果，就是成功经由 AdS/CFT 对偶描述了超流体到绝缘体的过渡 。此外还有另一项新兴的研究课题：流体/引力对偶，其中使用了 AdS/CFT 对偶来将流体动力学的问题转译成广义相对论的问题 。

通用化推广

三维引力

为了能更清楚了解四维宇宙引力的量子效应，有些物理学家对于维度较低的数学模型做研究，其中有两维空间及一维时间 。描述引力场的数学在这样的设定下变得简单得多，这样就可以使用熟悉的量子场论来研究量子引力，也就不需要出动弦理论或其他更尖端的手法来研究四维的量子引力 。

始于J·D·布朗和 马克·昂诺 （ 英语 ： Marc Henneaux ） 在1986年的研究 ，物理学家意识到三维时空的量子引力与二维的共形场论有着密切的关系。昂诺与同事于1995年更仔细地研究这种关系时，提出反德西特空间的三维引力相等于一种叫 刘维尔场论 （ 英语 ： Liouville field theory ） 的共形场论 。另一项由爱德华·维滕提出的假想指出，反德西特空间的三维引力相等于具怪兽群对称的共形场论 。这些假想就是 AdS/CFT 场论不需要全套弦理论或M理论的证据 。

dS/CFT对偶

现今宇宙会以愈来愈快的速度膨胀，而反德西特空间则与现今宇宙不一样──反德西特空间既不会膨胀，也不会收缩。它的大小在任何时间看起来都一样 。用较专门的术语来说，就是反德西特空间对应宇宙学常数为负的宇宙，而现今宇宙的宇宙学常数是一个微小的正数 。

尽管在短距离上引力与宇宙学常数的值应该没有很大的关联 ，但是能让 AdS/CFT 有一个宇宙学常数为正的版本还是一件好事。 安德鲁·斯特罗明格 （ 英语 ： Andrew Strominger ） 于2001年引入了对偶的新版本，叫 dS/CFT对偶 （ 英语 ： dS/CFT correspondence ） 。这项对偶的时空模型叫 德西特空间 （ 英语 ： de Sitter space ） ，其宇宙学常数为正。从宇宙学的观点来看，由于许多宇宙学家认为极早期的宇宙与德西特空间相近，因此这样的对偶是非常有意思的 。现今宇宙在遥远的未来也可能会与德西特空间类似 。

克尔/CFT对偶

尽管 AdS/CFT 对于研究黑洞性质是有用的 ，但是大部分用 AdS/CFT 对偶所考虑的黑洞在物理上并不现实。实际上就如上文所解释，大部分 AdS/CFT 的版本都需要用到带非自然对称的多维时空模型。

莫妮卡·桂卡（ Monica Guica ）、托马斯·哈特曼（ Thomas Hartman ）、宋维（ Wei Song ）和安德鲁·斯特罗明格于2009年成功证明 AdS/CFT 对偶还是可以用于研究天体物理学的黑洞。这项结果更精确地来说是可用于接近 极值 （ 英语 ： Extremal black hole ） 克尔黑洞的黑洞，这种黑洞的单位质量角动量是最大的 。他们成功证明这种黑洞能用相等的共形场论表示。克尔/CFT对偶后来延伸到角动量较低的黑洞 。

高自旋规范场论

AdS/CFT 对偶与另一对偶有着密切的关系，那个对偶是由伊戈尔·克列巴诺夫和亚历山大·泊里雅科夫于2002年所推测的 。该对偶指出反德西特空间中的某“高自旋规范场论”相等于带O(N)对称的共形场论。这理论的本体是一种描述任意高自旋粒子的规范场论。它于弦理论相近，因为弦的激发态可对应高自旋粒子。因此该对偶可能有助于研究 AdS/CFT 对偶的弦理论版本，和甚至可能证明 AdS/CFT 对偶 。西蒙尼·琼比（ Simone Giombi ）和尹希（ Xi Yin ）于2010年透过计算 三点函数 （ 英语 ： Correlation function (quantum field theory) ） 获得了更多该对偶的证据 。

参考文献

Aharony, Ofer; Bergman, Oren; Jafferis, Daniel Louis; Maldacena, Juan. N = 6 superconformal Chern-Simons-matter theories, M2-branes and their gravity duals. Journal of High Energy Physics. 2008, 2008 (10): 091.Bibcode:2008JHEP...10..091A. arXiv:0806.1218 . doi:10.1088/1126-6708/2008/10/091 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。