历史

傅里叶级数得名于法国数学家约瑟夫·傅里叶(1768年–1830年)，他提出任何函数都可以展开为三角级数。此前数学家如拉格朗日等已经找到了一些非周期函数的三角级数展开，而认定一个函数有三角级数展开之后，通过积分方法计算其系数的公式，欧拉、达朗贝尔和克莱罗早已发现，傅里叶的工作得到了丹尼尔·伯努利的赞助。傅里叶介入三角级数用来解热传导方程，其最初论文在1807年经拉格朗日、拉普拉斯和勒让德评审后被拒绝出版，他的现在被称为傅里叶逆转定理（英语：Fourier inversion theorem）的理论后来发表于1820年的《热的解析理论》中。将周期函数分解为简单振荡函数的总和的最早想法，可以追溯至公元前3世纪古代天文学家的均轮和本轮学说。

傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。

定义

在这一节中，s(x){\textstyle s(x)} 表示实变量 x{\textstyle x} 的一个函数，且 s{\textstyle s} 在 [x0,x0+P]{\textstyle [x_{0},x_{0}+P]}上可积， x0{\textstyle x_{0}} 和 P{\displaystyle P} 为实数。我们将尝试用谐波关系的正弦函数的无穷和或级数来表示该区间内的 s{\textstyle s} 。在区间外，级数以 P{\displaystyle P} 为周期（频率为 1/P{\displaystyle 1/P} ）。若 s{\textstyle s} 也具有该性质，则它的近似在整个实数线上有效。我们可以从有限求和（或部分和）开始：

sN(x){\displaystyle s_{N}(x)}  为周期为 P 的周期函数。运用恒等式：

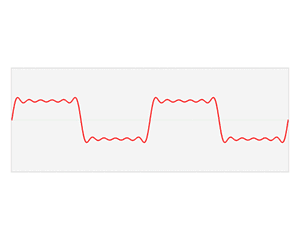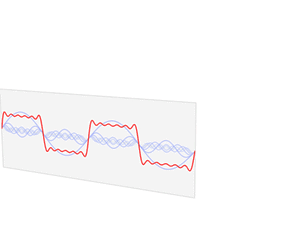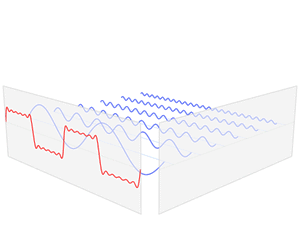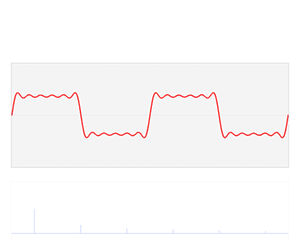
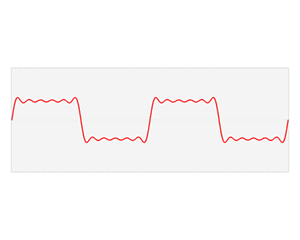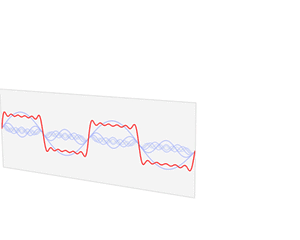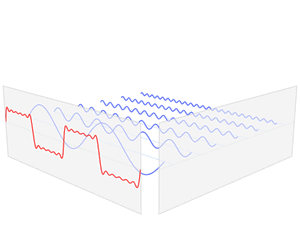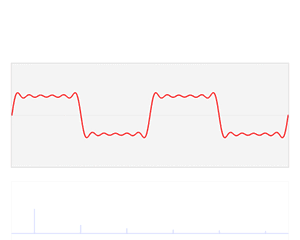
函数 s(x) （红色）是六个不同幅度的谐波关系的正弦函数的和。它们的和叫做傅里叶级数。傅里叶变换 S(f) （蓝色），针对幅度与频率进行描绘，显示出6种频率和它们的幅度。

我们还可以用这些等价形式书写这个函数：

其中：

当系数（即傅里叶系数）以下面方式计算时：

sN(x){\displaystyle s_{N}(x)}  在 [x0, x0+P]{\displaystyle [x_{0},\ x_{0}+P]} 近似了 s(x){\displaystyle s(x)} ，该近似程度会随着 N → ∞ 逐渐改善。这个无穷和s∞ ∞ -->(x){\displaystyle s_{\infty }(x)} 叫做 s{\displaystyle s} 的傅里叶级数表示。在工程应用中，一般假定傅里叶级数除了在不连续点以外处处收敛，原因是工程上遇到的函数比数学家提供的这个假定的反例表现更加良好。特别地，傅里叶级数绝对收敛且一致收敛于 s(x)，只要在 s(x) 的导数（或许不会处处存在）是平方可积的。  如果一个函数在区间 [x0, x0+P]上是平方可积的，那么此傅里叶级数在几乎所有点都收敛于该函数。傅里叶级数的收敛性取决于函数有限数量的极大值和极小值，这就是通常称为傅里叶级数的狄利克雷条件。参见傅里叶级数的收敛性（英语：Convergence of Fourier series）之一。对于广义函数或分布也可以用范数或弱收敛（英语：Weak convergence (Hilbert space)）定义傅里叶系数.

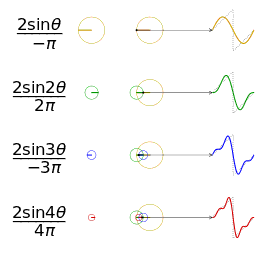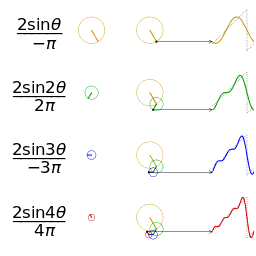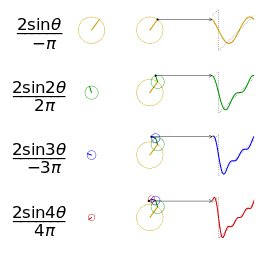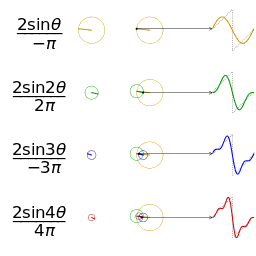
一个相同幅度和频率的锯齿波的近似的可视化

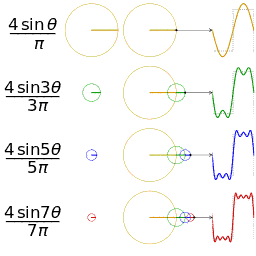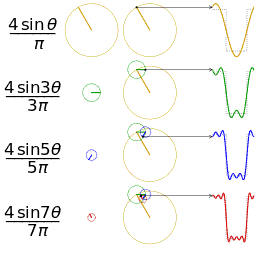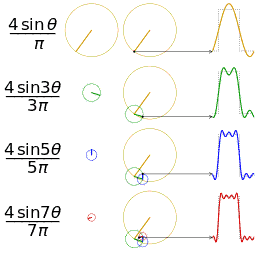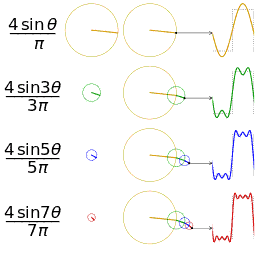
另一个分别采用傅里叶级数的前 1, 2, 3, 4 项近似方波的可视化。（可以在这里看到一个交互式的动画）

例1：一个简单的傅里叶级数

锯齿波周期函数的图

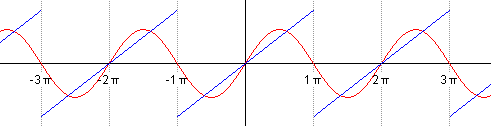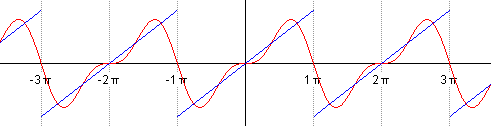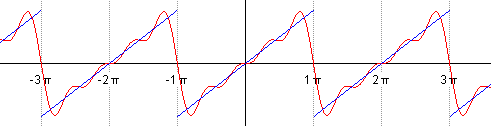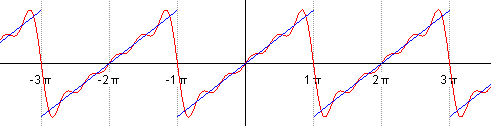
前五个部分傅里叶级数的动态图

我们现在用上面的公式给出一个简单函数的傅里叶级数展开式。考虑一个锯齿波

在这种情况下，傅里叶级数为

可以证明，当 s 可微时，傅立叶级数在每个点 x 都收敛于 s(x)，于是：

当 x = π 时，傅里叶级数收敛于 0，为在 x = π 处 s 的左极限和右极限之和的一半。这是傅里叶级数的狄利克雷定理的特例。

这个例子为我们引出了巴塞尔问题的一种解法。

例2：傅里叶诱导

金属板内的热分布，使用傅里叶方法求解

例1中我们的函数的傅里叶级数展开式看起来不比 s(x) = x/π 简单，因此人们需要傅里叶级数的原因也就不会立即显现出来。但还有很多应用，我们举用傅里叶诱导解热方程式的例子。考虑边长为 π 米的方形金属版，坐标为 (x, y) ∈ [0, π] × [0, π]。如果板内没有热源，并且四个边中三个都保持在 0 摄氏度，而第四条边 y = π，对于 x 属于 (0, π)，保持在温度梯度 T(x, π) = x 摄氏度，于是可以证明稳态热分布（或者说在很长一段时间过去后的热分布）为

这里，sinh 为双曲正弦函数。热方程的这个解是通过将 Eq.1 的每一项乘以 sinh(ny)/sinh(nπ) 得到的。我们示例的函数 s(x) 的傅里叶级数似乎很复杂，热分布 T(x, y) 是非平凡的。函数 T 不能写成解析解。用傅里叶的方法却可以求解这个热分布问题。

延伸

希尔伯特空间的解读

正弦和余弦形成了正交集合。正弦、余弦及其乘积的积分，当m与n不同或二函数不同时是0(绿色和红色区域相等抵消)，仅当m和n相等并且函数相同时为π。

所谓的两个不同向量正交是指它们的内积为0，这也就意味着这两个向量之间没有任何相关性,例如，在三维欧氏空间中，互相垂直的向量之间是正交的。事实上，正交是垂直在数学上的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关的，所以必然可以张成一个n维空间，也就是说，空间中的任何一个向量可以用它们来线性表出。

在希尔伯特空间释义下，函数的集合{en = e; n ∈ Z}是[−π, π]平方可积函数L([−π, π])的正交基。这个空间实际上是一个希尔伯特空间，有着针对任何两个的元素f和g的如下内积:

三角函数族的正交性用公式表示出来就是：

(这里的δmn是克罗内克函数)，而

傅里叶级数的收敛性

至今还没有判断傅里叶级数的收敛性充分必要条件，但是对于实际问题现的函数，有很多种判别条件可用于判断收敛性。比如x(t)的可微性或级数的一致收敛性。在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下：

在定义区间上，x(t)须绝对可积；

在任一有限区间中，x(t)只能取有限个极值点；

在任何有限区间上，x(t)只能有有限个第一类间断点。

满足以上条件的x(t)傅里叶级数都收敛，且：

1966年，里纳特·卡尔松证明了勒贝格二次可积函数的傅立叶级数一定是几乎处处收敛的，即级数在除了一个勒贝格零测集外均收敛。

吉布斯现象：在x(t)的不可导点上，如果我们只取(1)式右边的无穷级数中的有限项作和X(t)，那么X(t)在这些点上会有起伏。一个简单的例子是方波信号。

傅里叶级数的一些例子

参阅

离散时间傅里叶级数

傅里叶变换

维尔斯特拉斯逼近定理

参考文献

来源

电机电子类科《工程数学》，ISBN 978-957-584-377-9，作者 陈锡冠、曾致煌，高立出版社。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。